3.4 Etude paramétrique
Dans le but d'étudier la sensibilité du
comportement thermique et hydrodynamique ainsi que la performance thermique de
l'enceinte de MCP aux paramètres de contrôle, une étude
paramétrique a été menée. La présente
section expose et analyse les résultats des investigations
numériques mettant en évidence l'impact des paramètres de
contrôle suivants:
Ra, A, F , Ec, Es, A, ct s et ct
c .
Il faut noter que les valeurs de ces paramètres ont
été normalisées par rapport à celles de
références données aux Tableaux 3.1 et 3.2. La
normalisation de ces paramètres de contrôle a été
effectuée dans un souci de simplification des corrélations
numériques qui seront développées au chapitre suivant.
3.4.1 Analyse de l'effet du nombre de Rayleigh, Ra.
Le nombre de Rayleigh représente l'intensité de
la convection naturelle se manifestant dans la cavité du MCP liquide.
Dans la présente étude, ce nombre varie entre 6,27x108
et 5,01x109. Sa variation résulte de celle de la puissance
générée, par unité de longueur, Q' par chaque
source de chaleur (Q'E [7,5 W/m - 60 W/m]).
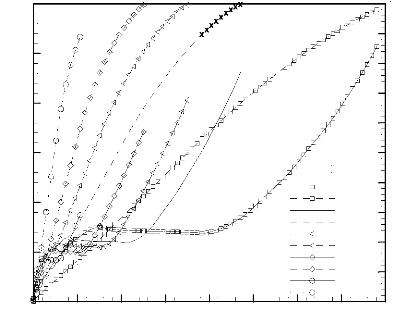
La Figure 3.6-a illustre la variation temporelle de la
température adimensionnelle maximale, O max , pour
différentes valeurs du nombre de Rayleigh. Comme il peut être
constaté, l'évolution temporelle de O max passe
par les mêmes phases que celles décrites à
la section précédente. La phase
intermédiaire représente le régime quasi- stationnaire
de
l'enceinte, durant laquelle la température maximale
adimensionnelle demeure pratiquement
constante. Sa durée est d'autant
plus courte que le nombre de Rayleigh est élevé. Il faut
T T m
--
noter que dans la définition de la température
adimensionnelle, O = A , le
T
terme ÄT comporte la puissance
générée, par unité de longueur, Q'. Celle-ci figure
aussi dans la définition du nombre de Rayleigh. En conséquence,
et afin d'élucider l'effet du nombre de Rayleigh sur le comportement
thermique de l'enceinte, il s'est avéré méthodique
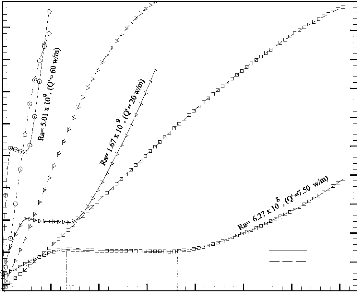
d'utiliser la température avec dimension, telle qu'illustrée
à la Figure 3.6.b.
èmax
0.12
0.08
0.06
0.04
0.02
0.1
0 X 0.80
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
X
X
X
X
X
X
X
X
X
X
XXXXXXXXXXXXXXXXX X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
Ra /Ra
0.125
0.233
0.333
0.5
1
ref
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
1
f

Figure 3.6 a: Effet du nombre de Rayleigh sur la
variation temporelle de la température maximale adimensionnelle (lignes
continues) et de la fraction liquide (lignes discontinues).
L'analyse de cette figure montre que la température
maximale enregistrée, lors du régime quasi- stationnaire, est
d'autant plus élevée que le nombre de Rayleigh est
élevé. Quant à l'effet de Ra sur la fraction liquide, la
figure montre clairement que la durée de fusion est d'autant plus courte
que Ra est élevé. De ce qui précède, il est clair
que l'accroissement du nombre de Rayleigh entraîne une surchauffe rapide
de la source de chaleur. En pratique, il y a des situations où la
puissance générée par le composant électronique est
telle que le nombre
de Rayleigh correspondant est relativement élevé
et la source de chaleur risque de surchauffer rapidement. Pour surmonter cette
difficulté la géométrie de l'enceinte ainsi que les
propriétés thermo- physiques de la plaque conductrice doivent
être optimisées de telle sorte à maximiser la durée
de fonctionnement sécurisé des sources de chaleur.
75.0
70.0
65.0
60.0
T °(C)
max
55.0
50.0
45.0
1
0.9 0.8 0.7 0.6 0.5 f 0.4 0.3 0.2 0.1
T f
ts1
ts2
40.0
35.0
0 5000 10000 15000 20000 25000 30000 35000
t(s)
Figure 3.6 b: Effet du nombre de Rayleigh sur la
variation temporelle de la température maximale Tmax (lignes
continues) et de la fraction liquide f (lignes discontinues)
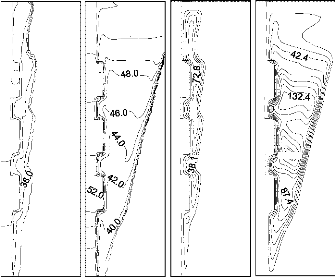
La Figure 3.7 illustre les lignes de courants et les
isothermes décrivant les champs hydrodynamique et thermique,
respectivement, pour deux valeurs du nombre de Rayleigh: Ra/Raref = 0,33 et
Ra/Raref = 1, à l'instant t = 2900 s.
Ra/ Ra ref= 0.33 Ra/ Ra ref= 1 Ra/ Ra ref= 0.33 Ra/ Ra ref= 1
36.0
T = 45.3 °C max
45.3
44.0
44.0
57.0
56.0
36.0
T = 57.6 °C
max
50.0
52.0
72.8
ø = 72.8
max
72.4
150.4
ø = 150.4
max
Figure 3.7: Isothermes et lignes de courants
pour Ra /Raref =0,33 et Ra/Raref = 1 (t = 2900 s)
L'analyse des lignes de courant montre que l'écoulement
induit par la convection naturelle se fait dans le sens horaire; ascendant au
niveau de la paroi chaude gauche et descendant le long du front de fusion
(paroi froide). Le volume de la cavité liquide est plus grand pour le
cas des nombres de Rayleigh élevés. Dans les deux cas du nombre
de Rayleigh, l'écoulement est multi cellulaire et la valeur maximale de
la fonction de courant, ø max ,
s'accroît avec l'augmentation du nombre de Rayleigh
à cause de l'augmentation de la différence de température
induisant l'écoulement. Par exemple, à l'instant t = 2900 s la
différence maximale de température est Tmax
-Tm = 9,3 °C et 21 °C, et la fraction liquide
correspondante f est 0,23 et 0,66 pour Ra/Raref =0,33 et
Ra/Raref =1, respectivement. La Figure 3.7 montre que, pour les
grandes valeurs de Ra (Ra/Raref =1), le champ thermique se stratifie
rapidement dans la partie supérieure de la cavité alors que pour
le cas des sources de chaleur à faible puissance, les isothermes sont
nettement inclinés. Pour les deux valeurs de
Ra, la température maximale est enregistrée par
la source de chaleur placée au sommet de la cavité. Cette
température est d'autant plus élevée que le nombre de
Rayleigh est élevé (Tmax = 45,3 °C pour Ra /Raref = 0,33 et
Tmax = 57 °C pour Ra /Raref = 1). Le nombre de cellules convectives
décroît avec le nombre de Rayleigh. Elles sont
déformées par les coins des blocs protubérants. En effet,
de point de vue hydrodynamique, la protubérance des sources de chaleur
est considérée comme un obstacle à l'écoulement; la
rugosité de la paroi chaude est importante avec l'existence des blocs
protubérants, comme il a été observé
expérimentalement par Ju et al.[43]. Dans la présente situation,
les trois faces des sources de chaleur, exposées à
l'écoulement du MCP liquide, transfèrent directement la chaleur
au MCP. Ce comportement est absent dans le cas où les sources sont
incrustées dans la paroi de la cavité (paroi chaude lisse)
[34].
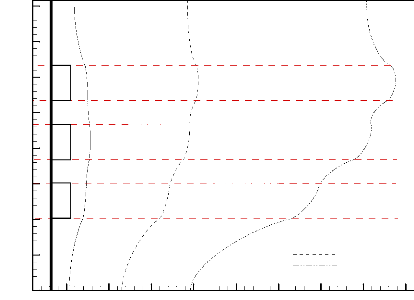
La Figure 3.8 met en évidence l'impact du nombre de
Rayleigh sur le profil de
température au sein de la plaque conductrice (milieu de la
plaque conductrice: E s
X= - ) à
2
l'instant t = 2900 s. Il ressort de l'analyse de cette figure
que la température s'accroît lorsque Ra augmente. Ceci est
dû au fait que la quantité de chaleur générée
par les sources de chaleur augmente avec Ra. Ainsi, pour une même
durée de stockage (t = 2900 s), le substrat stocke plus de chaleur
sensible pour les valeurs élevées de Ra. Un autre résultat
qui se dégage de l'analyse de la Figure 3.8 est que pour des valeurs
relativement faibles de Ra (Ra/Raref = 0,125), le gradient de
température vertical est faible en raison du transfert de chaleur
conductif qui prévaut dans la couche du MCP liquide avoisinant la paroi
chaude. Au fur et à mesure que Ra augmente, la convection naturelle
s'intensifie et le profil de température devient tributaire de la
structure de l'écoulement dans la phase liquide du MCP. On peut
constater, en particulier, le refroidissement relatif de la partie
inférieure du substrat et de la source de chaleur inférieure.
Y
0.75
0.25
1.75
1.25
0.5
1.5
2
0
1
S
S
S1
37.5 40 42.5 45 47.5 50 52.5 55 57.5
2
3
0,125 (7,5 W/m) 0,33 (20 W/m) 1,00 (60 W/m)
Ra /Raref
T(°C)
Figure 3.8: Profil de température au sein
du substrat (t = 2900 s, Es
X= - )
2
En effet, lorsque Ra augmente, les courants convectifs
impactant les faces des sources de chaleur et du substrat chaudes forcent le
liquide à extraire plus de chaleur au niveau de la partie
inférieure de la cavité et de la véhiculer, ensuite, vers
les zones supérieures de la cavité. Il en résulte une
remarquable montée en température dans la partie
supérieure de la plaque conductrice, en particulier au niveau de la
source de chaleur supérieure. Pour ce cas, la plaque conductrice n'est
plus isotherme, et la différence de température
enregistrée au sein de la plaque conductrice dépasse 12
°C.
Le Tableau 3.5 donne, en termes de pourcentages, les flux de
chaleur dissipés par les différentes surfaces de la plaque
conductrice et par les faces des sources de chaleur (Figure 3.9), durant le
régime quasi permanent, pour trois valeurs du nombre de Rayleigh.
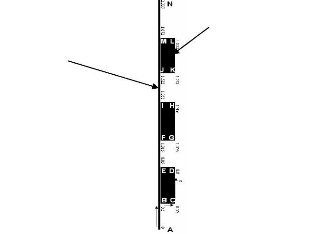
Plaque conductrice (substrat)
Source de chaleur (composant électronique)
Figure 3.9: Définition des
différentes surfaces de la paroi gauche (interface séparant le
MCP liquide et la paroi gauche)
Tableau 3.5: Contribution, en régime
quasi- permanent, des différentes surfaces de la paroi gauche au
transfert de chaleur (exprimée en % de la puissance
générée par les sources de chaleur).
Ra/ Raref 0,125 0,33 1
AB
BCDE (S1)
EF
FGHI (S2)
IJ
JKLM (S3)
MN
Flux de chaleur évacué par les trois sources de
chaleur vers le MCP
Flux de chaleur évacué par la plaque vers le MCP
Chaleur sensible stockée dans la plaque conductrice
Chaleur sensible stockée dans les sources de chaleur
Chaleur stockée par le MCP
22,04
|
%
|
20,34
|
%
|
18,74
|
%
|
|
19,10
|
%
|
18,95
|
%
|
18,63
|
%
|
|
7,00
|
%
|
7,26
|
%
|
7,24
|
%
|
|
19,56
|
%
|
19,60
|
%
|
19,85
|
%
|
|
6,10
|
%
|
6,42
|
%
|
6,78
|
%
|
|
16,76
|
%
|
17,02
|
%
|
17,30
|
%
|
|
7,70
|
%
|
8,05
|
%
|
8,50
|
%
|
|
55,42
|
%
|
55,57
|
%
|
55,78
|
%
|
|
42,84
|
%
|
42,07
|
%
|
41,26
|
%
|
|
0,62
|
%
|
0,93
|
%
|
1,13
|
%
|
|
0,47
|
%
|
0,61
|
%
|
0,70
|
%
|
|
98,26
|
%
|
97,64
|
%
|
97,04
|
%
|
L'analyse des données du Tableau 3.5 montre que la
contribution au transfert de chaleur des surfaces des sources (BCDE), (FGHI) et
(JKLM) vers le MCP liquide varie légèrement avec le nombre de
Rayleigh. Les portions de la plaque conductrice situées entre les
sources de chaleur, (EF), (IJ) et la portion supérieure (MN)
transfèrent moins de chaleur au MCP en comparaison avec la portion
inférieure de la plaque (AB). Il ressort aussi de l'analyse du Tableau
3.5 que, pour la plage considérée du nombre de Rayleigh, plus de
41 % de la puissance générée par les sources de chaleur
est transférée à la plaque conductrice et
convectée, ensuite, au MCP liquide au travers les faces (AB), (EF), (IJ)
et (MN), alors qu'environ 55 % de la puissance générée par
les sources de chaleur est transférée au MCP à travers
leurs surfaces exposées à l'écoulement. En
conséquence, durant le régime quasi permanent, la fusion du MCP
absorbe plus de 97 % de la puissance générée par les
sources de chaleur. La température de ces dernières reste
constante pendant ce régime. Ceci est justifié par les valeurs
relativement faibles des énergies stockées sous forme sensible
par les sources de chaleur, la plaque conductrice et le MCP.
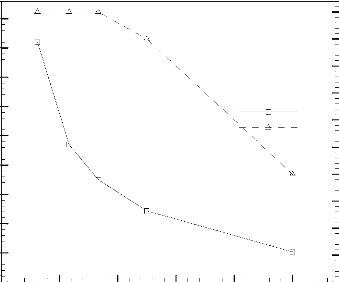
La Figure 3.10 donne la durée de fonctionnement
sécurisé, ô fonc , et la fraction liquide,
f, en fonction du nombre de Rayleigh. L'analyse de cette figure montre
que la durée ô fonc
diminue avec l'accroissement du nombre de Rayleigh. Pour les
faibles valeurs de Ra (Ra /Raref < 0,4) le MCP solide est totalement fondu
(f ~ 1) avant que la température maximale n'atteigne la
température critique, è cr .
ô
fonc
f
0.9 0.8 0.7 0.6
ô
fonc
0.5 0.4 0.3 0.2 0.1 0
0.98
0.96
0.94
0.92
f
0.9
0.88 0.86 0.84 0.82 0.8
0 0.2 0.4 0.6 0.8 1
Ra/ Raref
Figure 3.10: Durée de fonctionnement
sécurisé, ô fonc , et la fraction liquide
correspondante, f, en fonction du nombre de Rayleigh.
La Figure 3.10 permet de développer les
corrélations donnant la durée de fonctionnement
sécurisé, ôfonc , et la fraction liquide
correspondante, f, en fonction du rapport Ra /Raref:
0,6
,
~ ~
Ra
~ ~
Raref
ô fonc= - 0,186594 + 0,287894 ~ ~
2,7
~ l
Ra
f = 1,00273 - 0,134833 ~~ ~ (3.1)
~
Ra ref
avec 0,12 < Ra /Raref <
1,0
Le Tableau 3.6 montre un bon accord entre les résultats
numériques et ceux obtenus par les corrélations Eq. (3.1). Les
variations maximales pour ôfonc et f sont égales
à 6,45 % et
2,22 %, respectivement.
Tableau 3.6: Comparaison des résultats
numériques avec ceux obtenus par la corrélation Eq. (3.1).
|
Ra /Raref
|
ôfonc
numérique
|
ôfonc
corrélation
|
Variation
(%)
|
f
numérique
|
f
corrélation
|
Variation
(%)
|
|
0,125 0,23 0,333 0,50 1,00
|
0,819 0,470 0,351 0,244 0,101
|
0,81391 0,50064 0,36789 0,24777 0,09929
|
0,67 6,45 4,90 1,54 1,97
|
1,000 1,000 0,992 0,980 0,868
|
0,99789 0,98959 0,97947 0,95825 0,86790
|
0,21 1,04 1,26 2,22 0,01
|
|
|



