3.4.6 Effet de la distance adimensionnelle séparant
les sources de chaleur
Cette section présente les résultats relatifs
à l'effet de l'espacement sur le comportement thermique de l'enceinte
du MCP. Plusieurs simulations numériques ont été conduites
en considérant la marge de variation du rapport / ref : 0,5 - 2,2.
ô
0.6
f
0.5
0.035
0.015
0.005
0.03
0.01
X
0
0 0.02 0.04 0.06 0.08 0.1
Température limite adimensionnelle, cr
è
X
X
X X X X X
X
X
X
X
X
X
X
X
X
X
X
/
ref
X
X
2
2.2
0.5 0.8 1
1.3
1.7
0.9
0.8
0.7
0.4
0.3
0.2
0.1
1
0.025
è
max
0.02
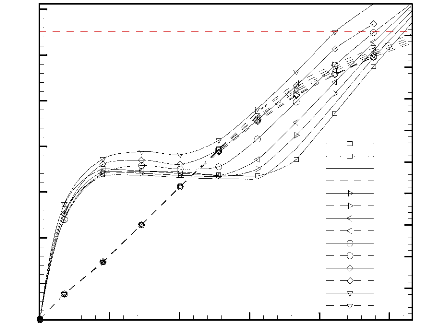
Figure 3.29: Effet de la distance
adimensionnelle / ref sur l'évolution temporelle de la
température maximale adimensionnelle (lignes continues) et
la fraction liquide (lignes discontinues).
La Figure 3.29 illustre l'évolution temporelle de la
température maximale adimensionnelle des sources de chaleur et de la
fraction liquide pour différentes valeurs du
rapport / ref . L'analyse de cette figure montre que
durant la première phase du processus
de fusion (dominée par la conduction thermique) la
montée en température est d'autant plus rapide que la distance
adimensionnelle est élevée. En effet, l'accroissement de la
distance adimensionnelle se traduit par l'éloignement des sources entre
elles. La fusion du MCP se manifeste essentiellement autour de chaque source de
chaleur. Ainsi, les zones liquides n'interfèrent pas rapidement et les
mouvements de convection naturelle deviennent moins intenses. Par
conséquent, le taux de transfert de chaleur évacué par les
sources de chaleur est réduit avec l'accroissement de . C'est la raison
pour laquelle la température adimensionnelle des sources de chaleur
augmente lorsque augmente. Quant à la durée du régime
quasi- stationnaire, elle est d'autant plus élevée que est
faible. En effet, pour les valeurs relativement élevées de , la
source de chaleur supérieure s'approche davantage de la paroi
supérieure adiabatique. La quantité du MCP emprisonnée
entre la paroi supérieure adiabatique et la source de chaleur
supérieure diminue. Ainsi, et après fusion de cette
quantité du MCP, la source de chaleur supérieure se trouve
rapidement entourée d'une zone liquide relativement chaude, à
cause des mouvements convectifs naturels se manifestant dans la cavité
liquide. Tous ces effets entraînent la réduction du gradient
thermique entre le MCP liquide et la source de chaleur supérieure. Cette
dernière stocke la chaleur sous forme sensible, ce qui se traduit par sa
rentrée précoce et rapide dans la troisième phase du
processus de fusion. Par ailleurs, le système évolue plus
rapidement vers l'état critique ( è max = è cr
),
pour les valeurs élevées du rapport /
ref . Il ressort aussi de la Figure 3.29 que la fraction
liquide
évolue linéairement et indépendamment du rapport /
ref , jusqu'à ce que le système
quitte le plateau et atteint la troisième phase du
processus de fusion. A partir de ce moment, la vitesse de fusion devient
tributaire du rapport / ref , sa valeur est d'autant petite que /
ref
est elevé.
La Figure 3.30 illustre le profil de température
adimensionnelle au sein de la plaque
conductrice ( Es
X= - ) pour différentes valeurs du rapport /
ref et pour trois différents
2
instants adimensionnels. Ces instants correspondent aux trois
principaux régimes du processus de fusion. Comme il peut être
constaté de l'analyse de cette figure, le maximum est situé
près de la source de chaleur supérieure quelque soit le rapport
/ ref , à l'exception de la première phase
(régime de conduction) où il est situé prés de la
source centrale pour / ref < 1.
1.5
Y
1
0.5
0
2
1.5
Y
1
0.5
2
1.5
Y 1
0.5
0
2
/
ref
0,5
1
2,2
ô=0,018
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
ô=0,051
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
0
ô=0,095
0 0.005 0.01 0.015 0.02 0.025 0.03 0.035
è
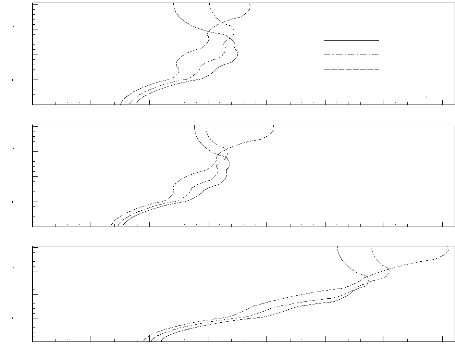
Figure 3.30: Profil de température
adimensionnelle au sein de la plaque pour différentes valeurs de la
distance adimensionnelle / ref ( Es
X= - ).
2
Il ressort, aussi, de l'analyse de ces figures qu'il faut
distinguer entre deux parties de la plaque conductrice: partie
inférieure (0 = Y = 1,7) et supérieure (Y > 1, 7 ). Dans la
partie
inférieure, la température adimensionnelle est
d'autant plus élevée que / ref est petit, alors que
c'est l'effet inverse qui se manifeste dans la partie supérieure.
Pour confirmer les constatations susmentionnées,
à la Figure 3.29, on analyse le Tableau 3.10 donnant la contribution, au
transfert de chaleur, des différentes surfaces de la paroi chaude,
exposées à l'écoulement, pour différentes valeurs
du rapport / ref à
l'instantô = 0,051. Ce tableau montre que la
plaque conductrice évacue plus de 35 % de la
puissance
générée par les sources de chaleur. L'accroissement du
rapport / ref cause une
réduction de la surface d'échange de la partie
supérieure de la plaque conductrice et par
conséquent une
réduction de sa contribution au transfert de chaleur (de 11,2 % à
0,08 % pour
/ ref = 0,5 et 2,2, respectivement). Ceci se traduit par une
surchauffe très rapide de la source
supérieure et, par la suite, une réduction de la
durée adimensionnelle de fonctionnement sécurisé.
Tableau 3.10: Effet du rapport /
ref sur la contribution des différentes surfaces
exposées
de la plaque conductrice et des sources de chaleur au transfert
de chaleur vers le MCP, ô = 0,051 (régime quasi stationnaire).
|
/ ref
|
Valeurs exprimées en % de la puissance
générée dans les sources de chaleur
|
|
0,5
|
20,64
|
20,50
|
3,08
|
18,80
|
2,55
|
17,80
|
11,20
|
|
0,8
|
19,31
|
18,8
|
5,90
|
18,10
|
5,40
|
17,90
|
9,55
|
|
1,0
|
18,74
|
18,63
|
7,24
|
19,85
|
6,78
|
17,30
|
8,50
|
|
1,7
|
16,63
|
16,20
|
12,80
|
19,50
|
13,40
|
17,00
|
0,12
|
|
2,2
|
16,35
|
15,80
|
13,62
|
19,40
|
15,40
|
16,50
|
0,08
|
S1 S2 S3
Plaque conductrice
La Figure 3.31 illustre la forme et la position du front de
fusion pour trois valeurs du rapport / ref à
l'instantô = 0,051. L'analyse de cette figure permet de
constater que pour
un rapport / ref faible, le front de fusion
progresse rapidement prés de la source de chaleur
supérieure. Ceci cause une déflexion de la forme
du front de fusion. Cette déflexion devient
moins prononcée
avec l'augmentation du rapport / ref ( / ref >1).
Il faut noter que pour
des valeurs élevées du rapport / ref
, le front de fusion intercepte la paroi adiabatique
verticale droite. Ainsi, le bloc du MCP solide, en face de la
source de chaleur supérieure, fond rapidement en causant la surchauffe
de celle-ci.

Figure 3.31: Forme et position du front de
fusion pour différents rapports / ref (ô =
0,051).
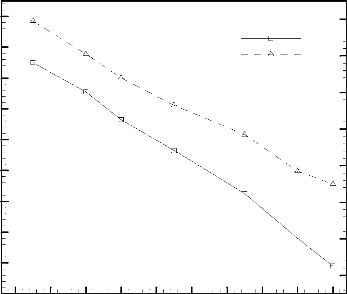
La Figure 3.32 relate l'effet du rapport / ref sur la
durée adimensionnelle de
fonctionnement sécurisé du
puits de chaleur, ôfonc , et la fraction liquide, f.
L'analyse de cette
figure montre que la durée adimensionnelle,
ôfonc , et la fraction liquide, f, sont d'autant
plus
élevées que les sources de chaleur sont plus
rapprochées. La durée ôfonc et la fraction
liquide, f, varient, approximativement,
linéairement avec le rapport / ref . Les
corrélations suivantes ont été établies:
~
~
ô = 0,1093 - 0,008 , = 0,9208 - 0,05277
~ ~ f ~ ~ (3.7)
fonc
~ ~
ref ~ ~
ref
avec 0,5 < / ref < 2,
2
La comparaison des résultats numériques avec
ceux obtenus à partir des corrélations Eq.(3.7), donnée
à la Figure 3.33, montre un bon accord. Les variations maximales sont
estimées à 3,5 %.
ô
fonc
f
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 2.2
/ ref
0.108
0.106 0.104
0.102
ô
fonc
0.1
0.098
0.096 0.094
0.092
0.09
0.9
0.88
0.86 0.84
f
0.82
0.8
0.78
0.76
Figure 3.32: Durée adimensionnelle de
fonctionnement sécurisé, ôfonc , et fraction
liquide, f, en fonction du rapport / ref
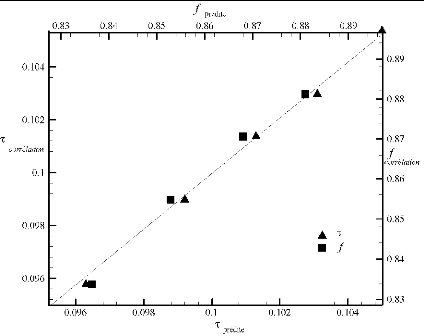
Figure 3.33: Courbe de parité.
| 


