2. 2. 9 Convergence
La nature des équations gouvernantes (couplage et non
linéarité des équations) nécessite un calcul
itératif. La convergence d'un tel calcul est déclarée
lorsque les trois critères suivants sont satisfaits:
- Critère mathématique:
|
~
|
k 1
+(i, j) (i, j)
- Ö k
Ö
|
|
i,j
|
|
|
|
|
< å
|
(2. 59)
|
|
~
i,j
|
Ö
|
k
|
(i, j)
|
où (i, j)
Ö k est la valeur de la variable
dépendante Ö ( è, U ou V) au noeud (i, j) à
l'itération
k. Le paramètre å doit être suffisamment petit
(= 10 -9).
- Critère physique traduisant la conservation de la masse
et de l'énergie:
Max ? in (i,j) -? out (i,j) < ~ m (2. 60)
1- (Q sen,s + Q sen,c + Q sen,l
+ Q lat ) < å T (2. 61)
où -8
å m =10 et å T= 10
-2
?in et ?out sont les
débits massiques adimensionnels entrant et sortant:
|
? (i,j) (U (i,j) AY V (i,j)
AX)
= + ~
in
~ ~
(i,j) (U (i 1,j) AY V (i,j 1)
AX)
+ + ~ ~
? = +
out
|
1 i M+1 ; 1 j N+1
= = = =
|
(2. 62)
|
La chaleur sensible stockée par la plaque conductrice, les
sources de chaleur et le MCP liquide sont exprimées par:
k 1
+ k
Q = ~ Ä Ä è - è ô (2. 63)
R X Y( ) / d
sen, s s
plaque conductrice
= ~ Ä Ä è - è ô (2. 64)
k 1
+ k
Q X Y( ) / d
sen, l
MCP liquide
k 1
+ k
Q = ~ Ä Ä è - è ô (2. 65)
R X Y( ) / d
sen, c c
source de chaleur 1,2,3
MCP
1 f
?
Q = ~ Ä Ä
X Y
lat Ste ?ô
(2. 66)
avec s p,s
ñ c ñ c
c p,c
R = ; R =
s c
ñ c ñ c
l p,l l p,l
2. 2. 10 Optimisation du maillage et du pas de temps
Afin de réaliser un compromis entre le temps de calcul
et la précision des résultats des simulations numériques,
une étude d'optimisation du maillage et du pas de temps a
été faite. Aussi, l'effet du nombre maximal d'itérations
internes sur les résultats obtenus a été analysé.
En se basant sur les données de la configuration de
référence données au Tableau 3.3 du chapitre III, les
résultas des effets des pas de temps et d'espace sont donnés au
Tableau 2.3 et à la Figure 2.5.
Le Tableau 2.3 donne l'effet de trois maillages
différents: 40x60, 60x80 et 80x100, sur la fraction liquide et la
température adimensionnelle maximale, à l'instant ô
= 0,0343. Le pas de temps choisi étant -4
~~ = 4,42x 10(20 s). L'effet du maillage sur
la durée adimensionnelle de fonctionnement sécurisé,
ôfonc (è max = è cr) et la fraction
liquide correspondante, f, est aussi
donné dans ce tableau. Comme on peut l'observer, le
passage du maillage de 60x80 à 80x100, entraîne des variations
relatives de la fraction liquide et de la température maximale
adimensionnelle de l'ordre de 0,82 % et 0,76 %, respectivement. Quant à
la durée maximale de fonctionnement sécurisé,
ôfonc , et la fraction liquide correspondante, f, les
variations
maximales sont estimées à 0,04 % et 0,11 %,
respectivement. Pour confirmer ces résultats, on a analysé
l'effet du maillage sur la position du front de fusion. Visuellement, la Figure
2.5.a montre que les fronts de fusion sont pratiquement confondus pour ces deux
maillages.
Tableau 2.3: Effet du maillage (a) et du pas
de temps (b) sur les résultats

èmax
ôfonc
M x N
Variation
relative
(%)
Variation
relative
(%)
Variation
relative
(%)
Variation
relative
(%)
f
(ô = 0,0343)
(ô = 0,0343)
(è max = è cr)
f
(è max = è cr)
Variation
relative
Variation
relative
Variation
relative
Variation
relative
èmax
f
ôfonc
f
Äô
40x60 0,3290 - 0, 01956 - 0,0964 - 0,801
60x80 0,3502 6,44 0, 01705 12,83 0,1013 4,83 0,868 7,72
80x100 0,3569 0,82 0, 01694 0,76 0,10134 0,04 0,869 0,11
(a, Äô = 4,42 x 10-4)
|
(ô = 0,0343)
|
(%)
|
(ô = 0,0343)
|
(%)
|
(è max = è cr )
|
(%)
|
(è max = è cr)
|
(%)
|
|
1,32x10-3 (60 s)
|
0, 3931
|
-
|
0, 01948
|
-
|
0,07250
|
-
|
0,758
|
-
|
|
7,73x10-4 (35 s)
|
0,3622
|
7,86
|
0,01772
|
9,03
|
0,08992
|
19,37
|
0,825
|
8,12
|
|
4,42x 10-4 (20 s)
|
0,3502
|
3,31
|
0,01705
|
3,78
|
0,10130
|
11,24
|
0,868
|
4,95
|
|
2,21x10-4 (10 s)
|
0, 3490
|
0,34
|
0,016970
|
0,46
|
0,10191
|
0,59
|
0,869
|
0,16
|
(c, M x N= 60x80)
Le Tableau 2.3.b montre que les pas de temps 4
~~ 4,42x10-
= et
At = 2,21x 10conduisent à des
variations relatives de la fraction liquide, de la température
-4
adimensionnelle maximale, de la durée adimensionnelle de
fonctionnement sécurisé, ôfonc ,
(è max = è cr) et de la fraction
liquide correspondante, f, de l'ordre de 0,34 %, 0,46 %, 0,59 % et
0,16 %, respectivement. La Figure 2.5.b montre que les fronts de fusion sont
pratiquement confondus pour des pas de temps inférieurs ( At
4,42x10- 4
= ).
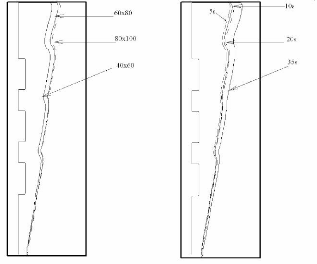
(a, Äô =4,42 x 10-4) (b: 60x80)
Figure 2.5: Effet du maillage, (a) et du pas de
temps, (b) sur la position du front de fusion, à l'instant ô =
0,0343
En conclusion, l'analyse des Tableaux 2.3 a et 2.3 b et des
Figures 2.5 a et 2.5 b
permet de conclure qu'un maillage de 60x80 et un pas
de temps 4
~~ 4,42x10-
= (20 s) sont
suffisants pour avoir des résultas insensibles aux pas
de temps et d'espace. D'autres pas de temps et d'espace ont été
testés, ces pas nécessitent une durée d'exécution
de calcul relativement longue sans, toutefois, apporter des variations
appréciables aux résultas.
Itérations internes:
Pour chaque variable Ö et pour chaque pas de temps, il
faut itérer jusqu'à résoudre le couplage spatial. A cet
effet, il faut que les itérations internes soient poursuivies
jusqu'à ce que la somme des résidus absolus soit réduite
à un niveau fixé, ou que le nombre maximal d'itérations
soit atteint. Le Tableau 2.4 donne l'effet du nombre maximum
d'itérations sur les résultats des simulations numériques,
en se basant sur les données de la configuration de
référence indiquées au Tableau 3.3 du Chapitre III.
Tableau 2.4: Effet du nombre maximal
d'itérations internes sur la fraction liquide, f, et la
durée adimensionnelle de fonctionnement sécurisé,
ôfonc
|
Nombre
d'itérations
|
f
( è max = è cr)
|
Variation relative
(%)
|
ôfonc
(è max = è cr)
|
Variation relative
(%)
|
|
5
|
0,7203
|
-
|
0,1140
|
-
|
|
7
|
0,7910
|
8,94
|
0,1075
|
6,05
|
|
10
|
0,853
|
7,27
|
0,1025
|
4,88
|
|
15
|
0,8685
|
1,78
|
0,1013
|
1,18
|
|
20
|
0,8700
|
0,17
|
0,1018
|
0,49
|
L'analyse des résultats obtenus montre qu'un nombre
maximal d'itération internes égale à 15 est suffisant pour
avoir des résultats précis. En effet, si on augmente le nombre
maximal d'itérations à 20, les variations relatives respectives
de la fraction liquide, f, et la durée adimensionnelle de
fonctionnement sécurisé, ôfonc sont égales
à 0,17 % et 0,5 %.
Les équations algébriques résultantes
sont résolues en utilisant l'algorithme de Thomas (TDMA), pour chaque
pas de temps. La durée d'exécution d'une simulation
numérique dépend directement du maillage et du pas de temps
utilisés. Le contrôle du nombre maximal d'itérations
internes permet de réaliser un compromis entre le temps de calcul et la
précision des résultats. La durée d'une simulation typique
(jusqu'à ce que è max = è cr (Tmax = Tcr)) est de
l'ordre de 9 heures de calcul itératif sur un ordinateur
de bureau équipé d'un microprocesseur 2.6 GHz avec 1 Gb de
RAM.
|
|



