Etude des transferts de chaleur dans une enceinte confinant un matériau à changement de phase et chauffée par des sources de chaleur protubérantes sur une paroi conductrice verticale

2.3 Validation du modèle numérique

2.3.1 Validation par l'expérience de Gau et al. [58]

Dans un premier temps, les résultats du présent code numérique, élaboré en Fortran, sont comparés avec ceux obtenus par Gau et al. [58] relatifs au problème bidimensionnel de changement de phase en présence de la convection naturelle dans une enceinte rectangulaire. L'enceinte utilisée dans cette expérience est de hauteur 6,35 cm et de largeur 8,89 cm. Les parois horizontales sont adiabatiques tandis que les deux parois verticales sont portées à des températures constantes; la paroi chaude est portée à 311,15 K et la paroi froide est maintenue à 302,93 K. Initialement, la cavité est remplie de Gallium pur à l'état solide, à la même température que la paroi froide. Les propriétés thermo physiques du Galium sont données dans le Tableau 2.5. La durée de l'expérience de la fusion du Galium est égale à 20 minutes. Le code de calcul est adapté aux conditions de cette expérience. La comparaison entre les prédictions numériques de la position du front de fusion avec les résultats expérimentaux est présentée à la Figure 2.6.

Tableau 2.5: Propriétés thermophysiques du Galium [59]

Tf (K) k ( W/m K) c_p (J/kg K) ñ _m (kg/m³) ì (kg/m s) â ( K^-1) AHf (J/kg)

302,93 32 381,5 6093 1,81x10^-3 1,2 x10^-4 80,16x10³

L'analyse de la Figure 2.6 montre que l'accord entre les prédictions numériques et l'expérience est satisfaisant; le faible écart observé peut être expliqué par l'instabilité de la température des parois du montage expérimental. En effet, Gau et al. [58] signalent que la température des parois n'a pas pu être réellement maintenue constante pendant l'expérience.

1

0.8

y/l 0.6

0.4

0.2

0

6 min 10 min 19 min

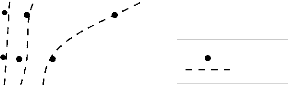
Expérience
Numérique

0 0.2 0.4 0.6 0.8 1 1.2 1.4

x/l

Figure 2.6: Comparaison entre les prédictions numériques de la position du front de fusion et les résultats expérimentaux de Gau et al. [58].

2.3.2 Validation par l'expérience de Ju et al. [43]

Le problème de fusion d'un MCP dans une enceinte chauffée par trois sources de chaleur protubérantes sur une paroi verticale (Figure 2.7) a été étudié expérimentalement par Ju et al. [43]. Le transfert de chaleur se fait par conduction dans les sources de chaleur et par conduction et convection naturelle dans la phase liquide du MCP.

Tableau 2.6: Propriétés thermo physiques du n-octadecane [61-63]

Tf (K)

km,s (W/m K)

km,l (W/m K)

(c p ) m,s (J/kg K)

(c p ) m,l (J/kg K)

ñm (kg/m^3)

ì (kg/m s)

AHf â (K^-1) (J/ kg)

301,16 0,38 0,15 1891 2251 771, 2 3,6x10^-3 9,1x10^-4 2,434x10⁵

w

			air
	ec
		l c ã	n-octadecane
	ä

l

e_s

Figure 2.7: Configuration expérimentale de Ju et al. [43]

L'enceinte utilisée dans cette expérience est similaire à celle étudiée dans le présent travail. Elle a une hauteur, l = 0,09 m, une largeur, w = 0,06 m, et une profondeur de 0,06 m. L'enceinte est chauffée par trois sources de chaleur, d'épaisseur, e_c=0,009 m, et de hauteur, l_c=0,015 m, avec une densité de flux de 900 W/m², imposée à la face gauche de chaque source de chaleur. Les sources sont protubérantes sur une paroi verticale, en Plexiglas, non conductrice de chaleur, d'épaisseur, e_s=0,02 m. La source inférieure est placée à une distance, ä = 0,0075 m, de la paroi horizontale inférieure de la cavité. La distance entre deux sources consécutives est ã = 0,015 m. Initialement la cavité est remplie de MCP solide (noctadecane, Tf = 28 °C) et dont les propriétés thermophysiques sont présentées dans le Tableau 2.6. Une couche d'air ayant une épaisseur de 1 cm, est prévue pour l'expansion thermique du MCP liquide. Le rapport de forme de cette cavité vaut 1,5. Le code numérique est adapté aux conditions de cette expérience et après le raffinement du maillage (MxN = 40x60) et du pas de

temps ( Äô = 3,5 x 10 ), une comparaison entre les prédictions numériques du front de fusion

-4

et les résultats expérimentaux, pour différents instants est présentée à la Figure 2.8.

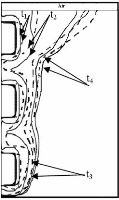
Figure 2.8: Comparaison entre les prédictions numériques (lignes continues) et les résultats expérimentaux [43] (lignes discontinues), t1 = 25 min, t2 = 50 min, t3 = 95 min et t4 = 110 min.

Compte tenu de la complexité des phénomènes mises en jeu lors de la fusion, l'accord entre les résultats numériques et l'expérience est satisfaisant. La concordance est bonne pour les instants t1 = 25 min et t2 = 50 min, excepté pour les zones supérieure et inférieure des sources inférieure et supérieure, respectivement. Ces sources semblent fournir moins de chaleur au MCP que prédit la simulation. Ceci peut être attribué aux pertes thermiques par les parois de l'enceinte, tout au long de l'expérience, à maintenir une densité de flux constante et uniforme pour les trois sources de chaleur ou lors de l'enlèvement de l'isolation au cours des prises des photos pour déterminer la position de l'interface. L'accord est satisfaisant pour les instants t3 = 95 min et t4 = 110 min, avec une déviation à droite du front expérimental dans la partie supérieure. Ceci est dû à l'expansion volumique du MCP au cours de la fusion, un effet dont le modèle ne tient pas compte. En effet, l'expansion du MCP provoque un débordement du liquide chaud à la surface libre du MCP solide, accélérant ainsi la fusion dans la partie supérieure. Aussi, une partie du liquide quitte le domaine de calcul en modifiant notablement

la condition à la limite nord (adiabatique dans le modèle). Il est donc normal d'observer un front de fusion `expérimental' plus avancé vers la droite.

Aussi, l'évolution temporelle de la température moyenne de chacune des trois sources de chaleur a été déterminée par la même expérience [43] et est comparée avec celle prédite par le code numérique. La comparaison est illustrée à la Figure 2.9. L'analyse d'une telle figure montre que l'accord est satisfaisant, en particulier pour t = 50 min. Cette période est caractérisée par la prédominance de la conduction thermique, les sources de chaleur ont pratiquement la même température moyenne. En effet, la puissance fournie à chaque source ne diffuse pratiquement pas au travers le Plexiglas à cause de sa faible conductivité thermique. En conséquence, la puissance fournie est stockée sous forme de chaleur sensible et cause l'accroissement des températures des sources de chaleur. Avec la progression de la fusion, les poches liquides entourant les sources de chaleur fusionnent et les mouvements convectifs se manifestent dans toute la région liquide. Ainsi, la puissance fournie aux sources de chaleur est évacuée par convection naturelle au MCP liquide; le système atteint, ainsi, un régime quasi stationnaire marqué par une stabilité des températures moyennes des sources de chaleur. Il est à noter que la différence des températures moyennes des sources de chaleur est expliquée par le fait qu'au début de la fusion les flux de chaleur évacués par les sources diminuent dans le sens ascendant. Ceci est dû à l'échauffement des particules liquides dans leur mouvement ascendant (T1= 34 °C, T2 = 35 °C et T3 = 38 °C). La Figure 2.9 montre que le présent code numérique reproduit fidèlement ce comportement physique. L'écart maximal enregistré entre les prédictions numériques et les résultats expérimentaux a été estimé à 2 %.

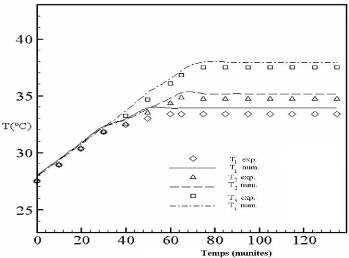
Figure 2.9: Evolutions temporelles des températures moyennes expérimentales et numériques des sources de chaleur.

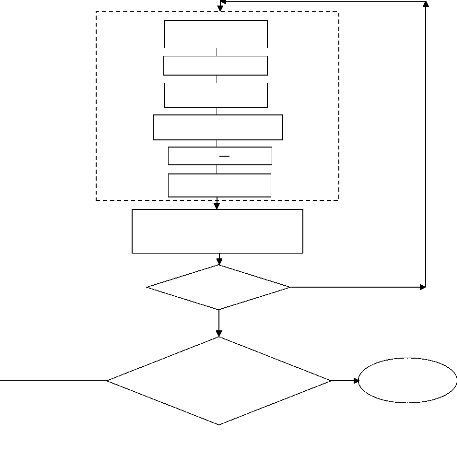
Correction P' et calcul de P

Calcul de è

Calcul de U

Calcul de V

Correction U'

Correction V'

Calcul de la nouvelle fraction liquide
f
et sa mise à jour

Convergence

Oui

cr

Oui Non

et

è < è

max

Fin

f

< 1

58

Non