Etude des transferts de chaleur dans une enceinte confinant un matériau à changement de phase et chauffée par des sources de chaleur protubérantes sur une paroi conductrice verticale

2. 2. 5 Méthode de résolution numérique

Le domaine de calcul est découpé en un ensemble de volumes de contrôle [56] entourant le point de maillage sur lequel l'équation générale (Eq. 2.20) est intégrée. Le volume de contrôle est centré sur le noeud (P) et délimité par les plans nord (n), sud (s), est (e) et ouest (w), comme illustré sur la Figure 2.2. Ces volumes sont égaux à ÄXÄY, ÄX et ÄY étant les pas d'espace selon les directions (x) et (y). Cette méthode préserve les propriétés de conservation des flux locaux et globaux, ce qui joue un rôle important dans la stabilité des calculs lors de la résolution numérique des équations.

				N
W		w	n			e	E
			s	P P
				S
	ÄY

ÄX

Figure 2.2: Volume de contrôle

En définissant les flux totaux (convectif et diffusif) comme suit:

J_x U

= Ö -

?Ö (2.32)

? X

?Ö

J_y V

= Ö ?

? (2.33)

Y

l'équation (2.20) devient alors:

?Ö ? J xJ y S

?

+ + = (2.34)

?ô ? X ?Y

L'intégration de l'équation générale Eq.(2.34) sur le volume de contrôle de la Figure 2.2 donne:

.f

? ? J ?Ö

x y

? ~~ ? ~~ ?ô

J dXdY + dXdY (S - )dXdY

= Ö

X Y

v v v

(2.35)

(I) (II) (III)

les termes (I), (II) et (III) sont développés comme suit:

x _e y

n? J x

(I) = dXdY J J Y J

= - Ä = Ä

( )

x _w ys x _e yn

xe xw x

~ ~ ? x

(II)

y

(2.36)

= Li ^y dXdY = ( J yn - J ys ) Ä X = ÄJ

x _w ys

?^?Jy

x y

e n 0

?Ö ~ Ö - Ö ~

P P

(III) (S- )dXdY S Ö

= ~ ~ = ~ - ~ Ä Ä

X Y

w s

y

?ô ~ Äô ~

x

avec

~ Ä = - X x x e w ~ ~Ä = - Y y y n s

et Äô désigne le pas de temps adimensionnel

Ö _p et o

Ö _P sont les valeurs de la variable 0 au point P respectivement aux instants actuel ô et

précédent ô-Äô. Le terme SÖ est la valeur moyenne du terme source sur le volume de
contrôle. Il dépend de Ö et il faut l'exprimer d'une manière linéaire afin de l'utiliser dans le

système d'équations linéaires ( S Ö = S _c + S_P Ö _P ). Le terme S_P doit être négatif afin d'assurer la

stabilité de la solution et une convergence rapide [56].

Pour établir les expressions des différents coefficients, les différents flux aux faces du volume de contrôle, peuvent être approximés par un schéma centré:

~ Ö+ Ö ~ ~ Ö - Ö ~

E P E P

J U ~ - ~

xe ~

e e ~

~ 2 ~ ~ X -X

E P ~

~ Ö + Ö ~ ~ Ö - Ö ~

W P P W

xw ~ ~ - ~ ~

w w

~ 2 ~ ~ X -X

P W ~

J U

(2.37)

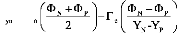
yn ~ ~

n n

J V

~ Ö + Ö ~ ~ Ö - Ö ~

S P P S

J V

ys ~ ~ ? ~ ~

s s

~ 2 ~ ~Y _P -YS

En remplaçant les flux par leurs expressions dans l'équation (2.35) et après réarrangement sous la forme algébrique, on obtient:

a _P Ö P = a _E Ö _E + a _W Ö _W + a NÖ _N + a SÖ _S + b (2.38)

on pose

F_e = U _e ÄY, F_w = U _w ÄY , F_n = V_n ÄX, F_s = V_sÄX (2.39)

e w n s D Ä e = Y, D Ä = Y, D = Ä X, D Ä = X w n s Ä X Ä X Ä Y Ä Y e w n s

(2.40)

avec, ÄX e = X _E - X_P, ÄX w = X P - X_W , ÄY_n = Y_N - Y_P , ÄY_s = Y_P - Y_S

Alors, les coefficients affectant la variable Ö de l'équation (2.38) sont donnés comme suit:

F F F F

e w n s

a D

= - , a D

= + , a D

= - , a D

= + (2.41)

E e W w N n S s 2 2 2

2

Ä X Ä Y

a U Y U Y V X V X a a a a +

= Ä - Ä + Ä - Ä + + + + - Ä Ä

S X Y (2.42)

P e w n s E W N S P

Äô

En faisant appel à l'équation de continuité, Eq (2.1), on obtient:

U _e ÄY -- - U _w ÄY + V_n ÄX -- - V_sÄX = 0 (2.43)

~ Ö + Ö ~ ~ Ö ? Ö ~

N P N P

~ ? ~

~ 2 ~ ~ Y -Y

N P ~

alors:

ÄXÄY

a a a a a

= + + + + - Ä Ä

S X Y (2.44)

P E W N S P

Äô

0 b S X Y ~ Ä Ä ~ X Y = Ä Ä + ~ Ö c P ~ Äô ~

(2.45)

La discrétisation des termes diffusif et convectif permet d'exprimer les coefficients, a _P ,a _E ,a _W ,a _N et a_S par les relations suivantes [56]:

P_s

) Sup(0,F )

+ s

) Sup(0, F ) , a D A(

+ - =

n S s

a D A( P ) Sup(0, F ) , a D A( P

= + - =

E e e e W w w

a D A( P

=

N n n

) Sup(0,F )

+ w

(2.46)

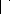
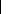
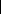
Tableau 2.2: La fonction A( P ) pour différents schémas.

Schéma Expression de A( P )

Différences Centrées 1 - 0,5 P

Upwind 1

Hybrid Sup(0,1 - 0,5 P )

5

P )

Sup(0,1 - 0,5

Loi de Puissance

F Le rapport i P = ^i D i

est le nombre de Peclet sur la face `i' du volume de contrôle,

exprimant le rapport du transfert de chaleur par convection à celui par diffusion. A( P ) est

une fonction qui dépend du schéma adopté pour la discrétisation des termes convectifs. Le
Tableau 2.2 donne les expressions de la fonction A( P ) pour les schémas fréquemment

utilisés. Patankar [56] a démontré que la réalité physique du problème exige que les
coefficients, a _P ,a _E ,a _W ,a _N et aS soient positifs ou nuls. Cette condition n'est pas toujours

vérifiée par le schéma centré quand le nombre de Peclet, P_e > 2 , c'est-à-dire, lorsque la

convection naturelle est intense et prédomine la diffusion. D'autres schémas sont proposés à savoir le schéma hybride et le schéma en loi de puissance. Ce dernier schéma est le plus recommandé dans la littérature [57]. Dans le présent travail, on a opté pour un schéma en loi de puissance. Les coefficients a _P ,a _E ,a _W ,a _N et aS de l'équation Eq. (3.45) sont ajustés en

remplaçant la fonction A( P ) par l'expression:

A( P

) = sup 0, 1 - 0,1 P ( ( )^5)

(2. 47)