2. 2. 4 Formulation adimensionnelle
Dans la présente étude les résultats
seront donnés sous une forme adimensionnelle. A cet effet, l'ensemble du
problème a été formulé à l'aide des
quantités représentatives sans dimension. Les équations et
les conditions aux limites et initiale seront adimensionnées en
utilisant les variables dépendantes et indépendantes et les
paramètres suivants:
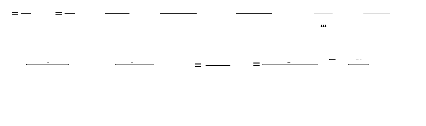
Ä = , T T f
3Q ' -
T è = ,
k Ä T
m
,l
v
á m,l o
/l
,
,
l o
x
l o
X
Y
y
, ô = ,
l 2
o
á u
m,l t U =
á m,l o
/ l
,
V=
=
g l T
â Ä
3
o
Ste
,
õ
m ,l
Pr
,
á
m ,l
f
Ä H
P
, ( / l ) 2
ñ á m,l o
p
m,l
, á =
á
Ra =
õ á
m,l m,l
c T
ml,p Ä
á
(2. 19)
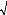
La quantité l o = lw - 3l c e c ,
représente la masse du MCP utilisée. Elle est retenue comme
longueur caractéristique.
Moyennant les quantités adimensionnées
susmentionnées, les équations gouvernantes
|
peuvent s'écrire sous la forme générale
adimensionnelle suivante:
2 2
? Ö ? Ö ? Ö
( ) U V ? Ö ? Ö
+ + = S
+
2 2
X Y X ? Y Ö
+
?ô ? ? ?
|
(2. 20)
|
Où est un coefficient de diffusion et SÖ
est un terme source associé à la variable
générale
Ö ( U, V ou è ). L'équation
générale se ramène donc à un terme d'accumulation
(terme d'inertie), un terme de convection, un terme de diffusion et un terme
source. Ces quantités sont explicitées au Tableau 2.1.
Tableau 2.1: Termes de l'équation
générale.
Ö SÖ
1 0 0
?
U Pr U
- +
P S
? X
?
V Pr V
- +
P S
? Y
è á Sè
|
avec,
|
( 1 f ) 2
-
S = - C U
U b f 3
+
|
(2. 21)
|
|
(1 f ) 2
-
S = - C V Ra Pr
+
V b f 3
+
|
è (2. 22)
|
~ 1 f
? ä "
2
S = ä ~ ä -
( )
1 + ~ (2. 23)
è 1 2
~ Ste ? ô 3E L
c c ~
L'équation (2.20) est soumise aux conditions aux limites
et initiale adimensionnelles suivantes:
- Conditions aux limites
- Frontières
adiabatiques
|
?è
? ç
|
paroi
|
= 0 où, frontière
ç ?
|
(2. 24)
|
|
|
|
- Interface plaque conductrice -( i ème) source
de chaleur
|
è = è
c
|
et K
s c
|
?è
|
|
|
K s
|
?è
|
|
|
(2. 25)
|
|
|
|
|
|
|
|
? X c
|
? X s
|
(X=0, i=1,2,3): Ä + (i - 1)( + L ) = Y = Ä + (i - 1) +
iL c
c
- Interface plaque conductrice - MCP
è = è
s
?è
?
s m
et K
m s
?è
? X
K m
X
(2. 26)
- Interface MCP- Source de chaleur
|
è = è
c
|
et K
m c
|
?è
? ç
|
c
|
Km
|
?è
? ç
|
m
|
(2. 27)
|
|
|
|
|
|
|
ç est la normale aux faces des sources de chaleur en
contact avec le MCP.
- Imperméabilité et non glissement sur les parois
solides
U=V=0 (2. 28)
Les propriétés thermo- physiques du MCP sont
évaluées comme suit:
K m = f + (1 - f) Km,s, á m = f + (1 - f) á m,s (2.
29)
Aux interfaces `i', entre deux matériaux
différents (MCP, plaque conductrice ou sources de chaleur), la
conductivité thermique adimensionnelle est estimée par la
méthode des moyennes harmoniques [56].
K K ( Ä + Ä)
+ - + -
K i
(2. 30)
K Ä + K
+
Ä
- - +
où, Ä + = ä + / l o est Ä - =
ä - / lo .
- Conditions initiales
è = U = V = f = 0 (2.31)
D'une manière générale, le système
peut être décrit, à partir de 5 groupements de
paramètres sans dimensions:
(1) Géométrie de l'enceinte:
Le rapport de forme de l'enceinte: A
~ 2 ~
~ + ~ ~ ~
~ ~
l CE
1 3
l o ~ ~ ~
Il est à noter que les dimensions adimensionnelles de la
cavité peuvent se déduire à partir des relations
suivantes:
L
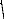
~ ~ + ~ ~ ~ ~ ~ ~ = ~ ~ t\
2
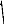
l CE
A 1 3 , W
~ ~ ~ ~
l A
o
~ ~
où, lCE représente le volume de la
source de chaleur.
(2) Dynamique de la fusion et de l'écoulement:
Ste, Ra
(3) Propriétés thermophysiques du MCP:
|
k a
m,s m,s
K = , ~ =
m,s m,s
k ~
m,l m,l
|
, Pr
|
(4) Caractéristiques des sources de chaleur:
k ~
c c
, K = , a =
c c
k ~
m,l m,l
e ä ã
E = , = , =

c Ä
c l l l
o o o
(5) Caractéristiques de la plaque conductrice:
e s
E = ,
s l
k a
s s
K = , a =
s s
k ~
m,l m,l
o
| 


