1.2 Efficience économique et
généralités sur les modèles de frontière
Si les dépenses sociales sont nécessaires pour
un accroissement potentiel du niveau de vie des populations, leur efficience en
est une autre non moins importante - si non plus importante- que les
autorités doivent promouvoir.
De façon générale, l'efficience
économique traduit la possibilité de produire une
quantité maximale à partir d'un input donné. Elle est
mesurée à partir de la relation entre la production
observée et la production maximale suite à l'utilisation de
l'input en question. On dira donc que les dépenses en services
socio-publics sont efficientes si la production de ces services est maximale.
Autrement dit, l'Etat ne peut produire, une fois que la
frontière d'efficience est atteinte, un niveau
d'output plus élevé que l'output efficient en réduisant
les dépenses engagées.
Il existe dans la littérature plusieurs techniques
d'estimation de cette frontière. Avant de passer en revue ces
différents modèles de frontière, nous allons d'abord
clarifié le concept d'efficience, un concept qui a fait l'objet de
beaucoup d'études théoriques et empiriques surtout dans le
domaine des dépenses publiques.
1.2.1 Clarification du concept d'efficience
La notion d'efficience productive ou économique est
différente de la notion d'efficacité sociale ou collective.
L'efficacité sociale ou collective est relative à l'ensemble
de l'économie qui inclut producteurs et consommateurs.
Elle est atteinte lorsqu'il est impossible d'accroître l'utilité
(ou la satisfaction) d'un consommateur sans détériorer celle d'un
autre. On parle alors d'optimum de Pareto ou optimum de premier rang
Pour définir ce concept d'efficience
économique, FARELL (1957) la décompose en une composante
allocative et une composante technique qui, selon DANIELA BORODAK (2007) se
décompose à son tour en efficience d'échelle et en
efficience technique pure.
1.2.1.1 Efficience technique et efficience
allocative
L'efficience allocative ou efficience des prix
provient de la capacité à combiner les inputs et les outputs
dans les proportions optimales, compte tenu des prix donnés sur le
marché. Elle évalue donc la façon dont la firme choisit
les proportions des différents inputs par rapport aux prix du
marché, supposé concurrentiel. Théoriquement, un processus
de production sera dit allocativement efficace si le taux marginal de
substitution (TMS) entre chaque paire de facteurs est égal à la
proportion des prix de ces derniers. Selon FARRELL (op.cit), l'inefficience
allocative stigmatise l'utilisation des inputs dans des proportions qui ne
correspondent pas à l'optimalité décrite par les prix
relatifs des inputs.
L'efficience technique ou efficience physique
concerne la capacité à éviter le gas-pillage (DANIELA
BORODAK, 2007). L'entreprise est donc déclarée techniquement
efficiente si, pour les niveaux d'inputs utilisés et d'outputs produits,
il lui est impossible d'augmenter la quantité d'un output sans augmenter
la quantité d'un ou plusieurs inputs ou de réduire la
quantité d'un autre output. L'efficience technique mesure la
manière dont une firme choisit les quantités d'inputs qui entrent
dans le processus de production, quand les proportions d'utilisation des
facteurs sont données.
Selon FARRELL l'inefficience technique correspond à
une production insuffisante par rapport à ce qui est techniquement
possible avec un niveau donné d'inputs.
Pour illustrer graphiquement ces concepts d'efficience,
FARRELL représente une fonction de production à deux facteurs de
la forme y = f(x1, x2), où y
représente l'output et (x1 , x2) les deux
facteurs considérés. Dans sa représentation, il suppose
que les rendements d'échelle sont constants, ce qui donne la forme
unitaire de la fonction (f(x' ,
x2 ) = 1) représentée à la
figure (1.1)
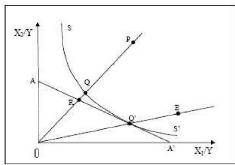
FIGURE 1.1 - Illustration de l'efficience technique et
allocative
SOURCE : Farrell,1957
Sur la figure (1.1), la courbe SS' désigne l'isoquant
et représente le lieu géométrique de l'ensemble des
possibilités de production. Cette courbe délimite, à sa
droite, l'ensemble des combinaisons d'inputs techniquement faisables. Selon
Farrell, l'efficience technique au point P est donnée par le
rapportOQ
OP . L'efficacité technique est
donc comprise entre 0 et 1 (OQ < OF). Tous les points situés
sur la frontière de production SS' sont techniquement efficients et ont
un score d'efficience technique égale à 1. Théoriquement,
pour être allocativement efficaces, les firmes doivent égaliser
leur taux marginal de substitution technique entre les deux inputs avec le
rapport des prix des inputs déterminés par le marché. La
droite (AA') représente graphiquement ce rapport des prix. Le point Q
correspond à la projection radiale de P sur la frontière SS'.
Ceci assure qu'il possède les mêmes proportions d'input que P.
Ainsi, pour FARRELL l'efficience allocative est déterminée par le
rapportOR
OQ. On voit donc, comme dans le cas de
l'efficience technique que l'efficience allocative est elle aussi comprise
entre 0 et 1 (OR < OQ). Tous les points situés sur
l'isocoût (AA') sont allocativement efficients mais ne sont pas tous
faisables. FARRELL, définit l'efficience économique comme une
combinaison de l'efficience technique (TE) et de l'efficience allocative (AE).
Cette efficience économique est obtenue au point Q' (Q' est à la
fois techniquement et allocativement efficace). L'efficience économique
au point P est égale au produit TE*AE = OQ/OP * OR/OQ = OR/OP. En
conséquence, le point P n'est ni techniquement ni allocativement
efficient. Le point Q, bien qu'il soit techniquement efficace, est
allocativement inefficace. Les points P et Q ont la même inefficience
allocative car ils utilisent leurs inputs dans les mêmes proportions.
Enfin le point E est allocativement efficient mais techniquement inefficient.
Cette inefficience technique peut être due à une inefficience
d'échelle ou à une inefficience technique pure.
| 


