Détermine la hauteur totale des couches
données, la hauteur de la première couche et le facteur de
progression pour les trois types suivants : [18]
> Linéaire
La hauteur de la couche particulière d'un prisme
est définie par :
H = h[1 + (n - 13(r - 13] (II. 4)
Avec:
h=hauteur initiale (initial height)
r=facteur de progression (height ratio)
n=nombre des couches (layer number)
La hauteur totale à la couche n est :
[(n - 13(r - 13 + 2]
ho = nh (II. 5)
2
> Exponentiel
La hauteur de la couche particulière d'un prisme
est définie par :
H = h * r(y-1) (II. 6)
La hauteur totale à la couche n est :
(1 - ri')
ho = h (1 - r) (II. 7)
> WB-Exponential
C'est la loi de croissance exponentielle est
définie dans l'ANSYS Workbench. La hauteur de la couche
particulière d'un prisme est définie par :
H = h * exp[(~_13(1_~3] (II. 83
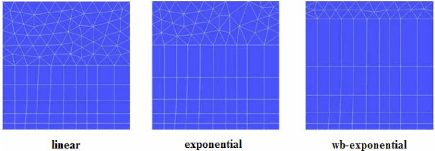
Figure (II.12) : Croissances des prismes. >
La hauteur initiale (Initial height)
Est la hauteur d'élément de la
première couche.
Si la hauteur initiale est placée à 0, la
maille d'entrée elle sera calculée automatiquement
> Facteur de progression (Height ratio)
Est le facteur de progression de la première
couche. Ce rapport sera multiplié par la taille d'élément
de la couche précédente pour définir la taille de la
prochaine couche.
> Nombres des couches de prisme (Number of layers)
Est le nombre de couches à développer.
> La hauteur totale (Total height)
Est la hauteur totale de toutes les couches de
prisme.
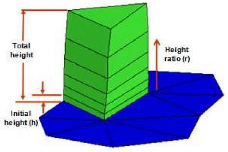
Figure (II.13) : Hauteur des prismes.



