II.4. Maillage hybride
II.4.1. Position du problème
Généralement on dit que, aucune des
techniques de génération automatique, telles qu'elles existent
aujourd'hui, ne peut seule respecter l'ensemble des critères
imposés à un maillage. Ainsi un bon maillage pour un programme
qui résout les équations de type Euler peut être de
mauvaise qualité pour un programme traitant les équations de type
Navier- Stokes. Dans le premier cas (Euler), il est fondamental d'avoir des
éléments qui ne soient pas aplatis alors que dans le second cas,
on demande un élancement important des éléments dans La
direction de L'écoulement.
La technique des maillages hybrides trouve sa
justification et sa motivation dans La tentative de résoudre cette
contrainte. Dans cette partie nous faisons d'abord un historique des maillages
hybrides, ensuite le processus de génération de maillage hybride
prismatique proche parois et ses déférentes lois
correspondantes.
II.4.2. Historique des maillages hybrides
Depuis la fin des années 80 les maillages
hybrides ont commencé à attirer l'attention des chercheurs comme
alternative à l'utilisation de maillages non structurés dans tout
le domaine. Dans l'approche non-structurée pure et pour avoir une
certaine
précision numérique, il faut utiliser
beaucoup de tétraèdres dans la région de la couche limite,
augmentant ainsi la probabilité d'avoir des éléments de
pauvre qualité connus sous le nom de Slivers à l'origine de
certaines imprécisions et singularités numériques. On a
don un impact direct négatif sur la précision, le temps de
calcul, et sur la robustesse des programmes informatiques dont le maillage est
le support. Les premiers résultats concrets dans cette nouvelle approche
de maillages hybrides datent de 1993 avec Nakahashi (1993) [15], Kallinderis et
Ward (1993) [16]. Marcum (1995) [17], par l'exemple que nous illustrons
ci-dessous montre que l'utilisation de quadrilatères à la place
de triangles au niveau de la couche limite, a pour effet à
précision numérique égale de réduire le nombre
d'éléments, donc le temps de calcul. Kallinderis (1995), montre
l'avantage de l'utilisation de maillage structurés par rapport aux non
structurés pour mieux capter la physique du problème dans la
couche limite, et réduire par la même occasion les temps de
calculs.
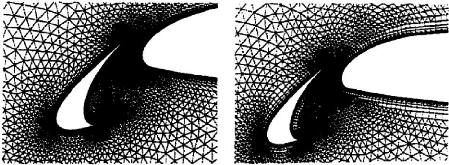
Figure (II.11): Exemple de Marcum (1995) faisant
passer le nombre de triangle de
11544 au niveau de la couche limite
(maillage non-structuré pur, figure à gauche) à
5772
quadrilatères (maillage hybride, figure à droite).
Pour des raisons d'espace mémoire, de vitesse
d'exécution, et le désir d'avoir des éléments
étirés à grand coefficient de forme, ils ont
proposé l'utilisation d'éléments prismatiques
structurés au niveau de la couche limite pour former le maillage, zone
ou les effets visqueux sont dominants, et d'éléments
tétraédriques à l'extérieur de la couche limite ou
l'écoulement est non visqueux.
| 


