Chapitre 4
odelisation bond graph
4.1 Introduction
Le modele bond graph a ete invente par H.Paynter en 1961 et
developpe ensuite par Karnopp et Rosenberg en 1983, Thoma en 1975 et 1991 et
Breedveld en 1984 [26]. C'est un outil unifie de modelisation des systemes
dynamiques et it permet la conception, la simulation et l'analyse des systemes
complexes. Il est totalement in-dependant du domaine auquel appartient le
systeme physique. C'est une reproduction graphique du systeme, en utilisant les
sommets et les liens pour representer respectivement les composants et les
relations definissant le systeme.
Dans ce chapitre, nous introduisons les fondements de base de
la modelisation bond graph comportant une classification des elements mono et
multiports ainsi la notion de la causalite. Le concept, chemin causal sera, par
la suite decrit en detail pour les bond graphs simples et les bond graphs
multiports.
4.2 Bond graphs simples
4.2.1 Les elements bond graph Le bond
Les elements bond graphs s'echangent l'energie a travers les
bonds. La puissance est le ratio de la derivee de l'energie par rapport au
temps ; la puissance est le produit de l'effort et du flux. Les directions des
deux variables flux et effort sont opposees. A partir de ces

0 1
i V
e f
P = ef
P
u F

p(t) = R 0
t
e(ô)d(ô)
q(t) = f0 t
f(ô)d(ô)
Z t
E(t) =
p(ô)d(ô)
0
|
|
|
|
|
|
e
|
i
|
F
|
q
|
|
F
|
v
|
p
|
x
|
|
t
|
w
|
H
|
q
|
|
P
|
Q
|
Pp
|
V
|
|
(R, C, I, Se, Sf)
(TF,GY ) (0,1)
p(0) q(0)
p(t)
q(t)

Se,Sf
0,1,TF,GY
R
ÖR(e,f) = 0
R
C
ÖC(e,q) = 0
R,C,I
C

I
Sf
Se
I
ÖI(p,f) = 0
R,C,I
0,1,TF,GY
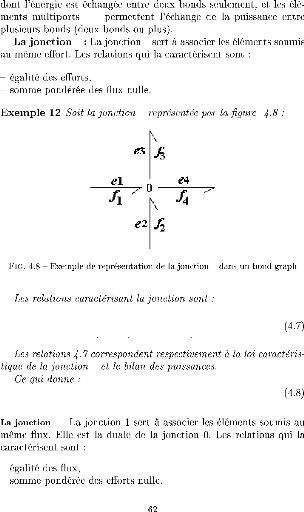
e1 = e2 =
e3 =
e4
e1f1 +
e2f2 -
e3f3 -
e4f4 = 0
0
f1 + f2 - f3
- f4 = 0
1
0, 1
0
0
0 0

e1 =
me2
f2 = mf1
0
1
f1 = f2 =
f3 =
f4
e1f1 +
e2f2 -
e3f3 -
e4f4 = 0
1
e1 + e2 - e3
- e4 = 0
TF
m
TF

e1 = rf2
e2 = rf1
0 1
A B A
B p = ef
A B
e A
f
A B f
e
GY
GY
r
FIG. 4.12 -- Position du trait causal au niveau d'un bond
Ces deux cas conduisent a deux schemas blocs differents,
illustres sur la figure 4.13.
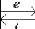
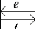
FIG. 4.13 -- Les deux differentes situations de la
causalite
Comme la position du trait causal est tout a fait
independante du sens de la demi-fleche, on obtient les deux cas illustres sur
la figure 4.14.
FIG. 4.14 -- Independance de la position du trait causal par
rapport au sens du bond
Les differents types de la causalite :
Ports avec causalites fixes : Ce sont les elements de sources
d'effort et de flux qui possedent une causalite fixe (voir figure 4.15).
Cependant, si l'objectif de noire analyse est la derivation du modele
mathematique (Equations d'etat), alors les elements non-lineaires seront
consideres comme des ports avec causalite fixe. C'est le cas ou la relation
constitutive de l'element non-lineaire ne peut pas etre exprimee par une forme
arbitraire de causalite.
Ports avec causalites preferees : Pour des considerations
d'ordre
numerique et souvent physique, it est plus aise d'integrer que de
de-
river, par consequent on essaiera d'affecter aux elements de stockage

I C
f CI e
eC = 1 f fcdt
C
eI = I dfI
dt
C I
e C I
f
fC = C deC
f eIdt
dt
fI = I 1
C I

e = Rf f R
f = e e R
R
R
TF GY 0 1
0
e2
e1 = e2, e3 =
e2, e4 = e2
f2 = --f1 +
f3 + f4
1 n
n -- 1

0
1
1
f1 = f2 = f3
= f4
e3 = e1 + e2
- e4
e1 - e2 - e3
- e4 = 0
0
f1 = f3, f2 =
f3, f4 = f3

1

0 1 TF GY
1 -
2 - 3 - 4 I
R
I R
E = {C, I, Se, Sf, De, Df}

{R,C,I}
I R 1 - 2 - 3
- 4 -
4 - 3 - 2 -
1

X p
I q C
1 - 5 - 5
- 1 4 - 3
- 6 - 6
- 3 - 4
xi xd
Xÿ X
ÿxi xi
ÿxd xd
Z f
I C
Zi Zd
Y
Din R
Dout R
S
ÿxi
|
|
S11
|
S12
|
S13
|
S14
|
Zi
|
Zd
|
=
|
S21
|
S22
|
S23
|
S24
|
ÿxd
|
Din
|
|
S31
|
S32
|
S33
|
S34
|
Dout
|
Y
|
|
S41
|
S42
|
S43
|
S44
|
U
|
|
U
S (nc
+ns) (nc
+ne)

nc (R,C,I)
ns
ne
Dout = L.Din
s 1/s
Zi = H(s)
ÿxi
Zd =
H'(1/s)
ÿxd
L H(s)
H'(1/s)
Se
Df De
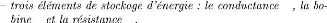
C
I R

(a) (b)

ÿxd = [f2,
e5]tÿxi =
[]t Zd =
[e2, f5]t
Zi = []tt
Dout[f4]tDin
= [e4]t
U
= [Se]t Yout
= [De, Df]t
V
= [Se, e2, e5,
e4, f5, f4,
f2, De, Df]t
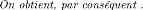

e2
f5
e4
Df
De
f2
e5
f4
Se
?
?
?
? =
Zd
Din
Y
?
0 --1 0 1
? 1 0 --1 0
?
= ? 0 1 0 0
? ?1 0 0 0
0 1 0 0
R CISe Sf De Df TF GY
0 1
R C I
C I
C C
n C
ime ÿqi
C
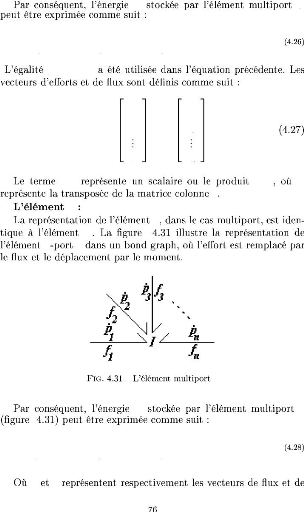
Z t >n Z t >n Z t
>n Z q
E = (eifi)dt
= (ei ÿqi)dt =
(eiq()dqi =
e(q)dq =
E(q)
t0 i=1 t0
i=1 t0 i=1
q0
q1
q2
q3
e1
e2
e3
q =
, e =
qn
en
Z t >n Z t >n Z t >:n Z
p
E = (fiei)dt
= (fi ÿpi)dt =
(fip()dpi =
f(p)dp =
E(p)
t0 t0 t0
p0
i=1 i=1
i=1
E C
fidt = dqi
edq etdq et
e
I
I
C
n I
I
E I
f p
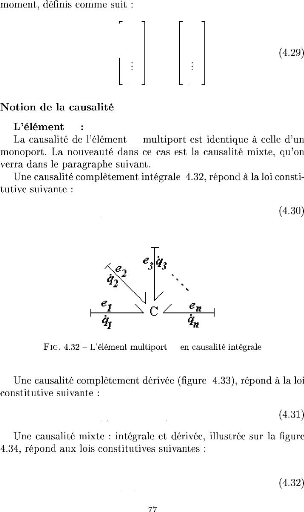
ei =
ÖCi(q1, q2,
· · · , qj, ej+1,· · · ,
en), i =
1,2,· · · ,j
f1
f2
f3
,f =
fn
C
ei = Ö-1
Ci
(q1,q2,···,qn),i
= 1,2,···,n
? p1
? p2 ?
p = ? p3
pn
C
C
qi =
ÖCi(e1,e2,··
· ,en),i =
1,2, · ··,n

qk = Ö-1
Ci (q1,
q2, · · ·, qj,
ej+1,···,
en),k = j,
2,··· ,m
C
C
I
I
C
fi = Ö-1
Ci
(p1,p2, · · ·
,pn), i = 1,2,
· · · ,m
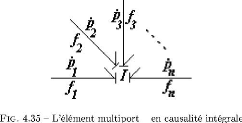
I
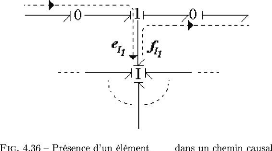
MP

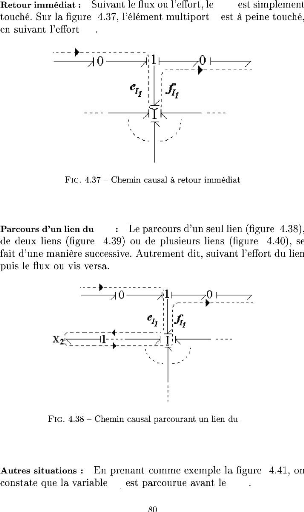
MP
MP
eI% MP
eI1
MP I
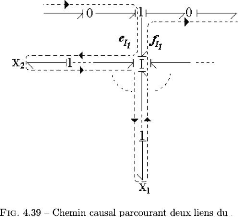
MP


MP
0 C0
MP
1 C1
MP
2 C2
MP
1 - 2 C1 -
2
MP
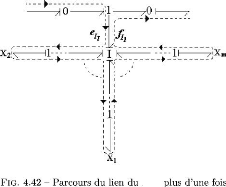
MP
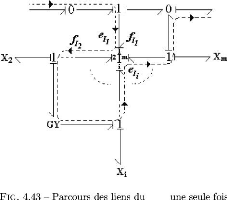
MP


MP
0 C0
MP
{R,C,I}
t Tt 1 < t <
dim(M) dim(M)
MP t
1 C1
MP
2 C2
MP
1-2 C1-2
MP
le cas des multiports, le probleme combinatoire de parcours
des chemins causaux est accentue. La notion de chemins causaux et leur
classification ont ete fournies par la suite afin de mieux aborder le chapitre
suivant.
| 


