Bond graphs couplés pour la surveillance

Chapitre 5

Contribution : Les bond

graphs couples et la

surveillance

5.1 Introduction

Il existe differentes methodes de generation de RRAs a partir d'un modele bond graph. Deux possibilites peuvent etre proposees pour la classification de ces methodes :

classification [29] en methodes directes et indirectes, classification [37] en methodes analytiques et structurelles.

Dans ce chapitre, nous allons presenter les differentes methodes appliquees dans la surveillance des systemes physiques. Nous presentons les methodes directes qui permettent une generation des RRAs directement du bond graph, et celles qui determinent les RRAs a partir d'un modele intermediaire. Nous exposons, par la suite, noire algorithme avec sa complexite. Nous decrivons la conception de l'algorithme [29] pour le graphe structure) et son extension vers les bond graphs simples et les bond graphs couples.

p

I

C

I C R

I q C

ABC D

R TF GY

?
????

1

?
?

D(s)

?

? =

De1

Df1

Df2

b1 M1

_s2

? ? ? ? ? ? ?

V1 F1 F2

? ?

(1+M2 s2

k1 )

--b1s b1M1 s3

k1 k2

k1 (1+b1 k1 s )

1 + b1 s (1 + M2 k1 s ) k1 s + (1 + b1 k1 s ) s s

k1 k1 k2

(1+b1 s (1+b1 k1 s +M1 s2

k1 )

1 + b1 k1 s + M1 s2 k1 )

s s

k1 k2 k2

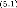
F2

F1 F2

V1F1 F2

V1F1

D(s) = 1 + M2s2

k2 + M1s2

k2 + M1s2

k1 + b1s

k1 + b1s

k1 (M2s2

k2 + M1s2

k2 ) + M1M2s4

k1k2

	De1	Df1	Df2	V1	F1		F2	Re1
1	0	0	1	1	1		Re2
0	1	0	1	1	1		Re3
0	0	1	1	1	1

~

-I -M'

~ S

M = I

Y

MT(s)

S

M

U

S11 ? ? S31 M =? ? S41 ? ? I1 ?0 0

S12 S22 S32 S42 0 I2 0

? ? S21 S13 S23 S33 S43 0 0 I3

S14 S24 S34 S44 0 0 0

-I1 0 0 0 -H(1/s) 0 0

0 -I2 0 0 0 -H^'(1/s) 0

0 0 -I3 0 0 0 -L

0 0 0 -I4 0 0 0

_M'

?

M'.V = 0

M

Mij

i j

(2m_c + m_s) 2m_c

m_s

I1I2I3 I4

M.V = 0

M

V

M

M 1

_M*

M*

F1 F5 F2 M* = F7 F8 F6 F3 F4

? ? ? ? ? ?

0 1 0 1 0 1 0 0

1 0 1 0 1 0 1 0

0 1 0 0 0 0 0 1

1 0 0 0 0 0 0 0

1 0 0 0 0 1 0 0

0 1 0 0 0 0 1 0

0 0 1 0 0 0 0 1

0 0 0 1 0 0 0 0

0 0 0 0 1 0 0 0

	Se	De		Df	Re1
1	1	0		Re2
0	1	1

0 1

0

1

0

1

0 1

0 1

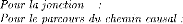
0 e2 = e1 - e3

e3 = De e1 = Se Df = (Cs)e2

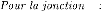
1 f5 = f3 - f4

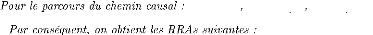
f3 = Df f4 = De/R De = (Is)f5

Df = Cs(Se - De) De = Is(Df - De/R)

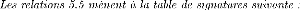
	Se	De		Df	Re1
1	1	1		Re2
0	1	1

1

	y1	y2	y3	· · ·		yn	Re1
1	1	0	· · ·	0		Re2
0	1	1	· · ·	0
				1		Ren
1	0	0	· · ·	1

CHEM

d d

q

q - 1

1 C

q

C[i,j] = 1 1

i j

C[i,j] = 0

1

_C,

sommet C'

sommet E K0

K0 = K0 - {sommet} K1 = K1 U {sommet}

NR = |K|

K0 = K1 = ö

sommet E K1

K1 = K1 - {sommet} K+ 2 = K+ 2 U {sommet}

C,	10	11	C, 1^+2
	d	f
			df

2

NR |K|

3 4

K0 0

K1 1

1

K+ = 2

2

l 1

i Kd

j Kf

? l i j

C

l 1

i Kdf

? l i i

C

l

d f

5

RRAs

K0 = K K1 = ö K+ 2 = ö

C

	Se	De	Df
C1	1	1	0
C2	1	0	1
C3	0	1	1

	Se	De	Df
Re1	1	1	0
Re2	1	0	1
Re2	0	1	1

C' N

sommet

1 N sommet E K0

sommet E K0 sommet E K0

sommet E K1

N * 3

O(N)

2

1 1 1

1 1

3

O(1)

l i j

1 N

l i

j O(N)

RRA

N

O(N) N *N *

N * (3N) O(N⁴)

O(N4)

{,,,,}

l i

i O(N)

l i

1 N

O(N)

N *N *

RRA

N

(3N) O(N³)

3

O(1)

C

O(N²) 5

O(N⁴) O(N³)

O(1)

_Ci _ime

Ca

_Ei _ime

Ce

C1 Ca= {Se, e2, f2, Df} C²Ca = {Se, e5, De}

C³Ca = {Df, f2, f5, e5, De}

E1 Ce= {Se, e2, f2, Df} E²Ce = {Se, e2, f2, f3, f5, e5, De}

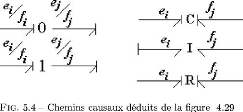
0	f(ei, ej) f(fi, fj)
1	f(ei, ej) f(fi, fj)
C	f(ei, fj)
I	f(fi, ej)
R	f(ei, fj)

Se De Df

MP

C

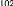
	Se	De	Df
C1	1	1	0
C2	1	0	1

	Se	De	Df
Re1	1	1	0
Re2	1	0	1
Re2	1	1	1

eh
et

e_c

?

E = ?

? ? ?

fh

? , F = ? ft ?

fc

fhft f_c

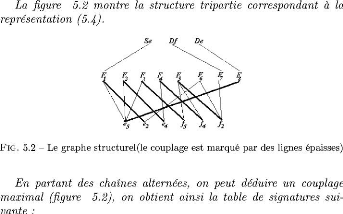
ehet e_c

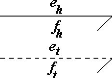
FIG. 5.7 -- Representation du couplage des energies par deux liens en pointilles et en trait plein

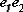
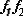
FIG. 5.8 -- Representation du couplage des energies par deux liens separes

Les bond graphs couples ne sont pas directement utilises comme support a la surveillance. Afin de generer les RRAs, des transformations doivent etre effectuees au niveau du bond grah couple. L'utilisation de la causalite integrals permet d'eviter les difficultes de calculs numeriques de la derivee du residu lors de la simulation.

Les methodes de redondance analytique et de l'analyse structurelle ont fait l'objet d'application a des processus thermofluides, tels que :

-- un generateur de vapeur,

un condensateur d'une installation pilote complexe representant le fonctionnement d'une centrale a echelle reduite.

Les deux approches initialement proposees [11], pour la surveillance

avec les bond graphs couples sont :

1. &coupler les liens couples en liens simples puis appliquer les outils déjà developpes pour les bond graphs monoenergie,

2. proposer une methode de linearisation des muliports permettant ensuite une analyse du bond graph par un parcours de chemins causaux generalises.

Notre but dans ce travail est de permettre la surveillance par les bond graphs couples sans transformations. Ceci en adaptant le nouvel algorithms (1' algorithme 5) directement sur le modele bond graph.

_Xn
i=1

Ö_s : mÿ +

ai ÿmi = 0

^ÿH)

_Xn
i=1

ai ÿmi = 0

_ö-1

h (P, ^ÿH) +

Pn i=1 ai ÿmi

R C I RRA

0h

ai #177;1

mÿ
Hÿ

C

Öb : P = öh( ÿm,

ÿmi (i = 1 · m)

mÿ

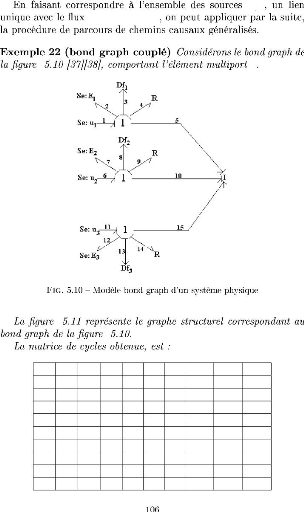
Sfh

fh = Pn i=1 ai ÿmi

I

	E1	E2	E3	u1	u2	u3	Df1	Df2	Df3
C1	1	0	0	1	0	0	1	0	0
C2	1	0	0	1	0	0	0	1	0
C3	1	0	0	1	0	0	0	0	1
C4	0	1	0	0	1	0	1	0	0
C5	0	1	0	0	1	0	0	1	0
C6	0	1	0	0	1	0	0	0	1
C7	0	0	1	0	0	1	1	0	0
C8	0	0	1	0	0	1	0	1	0
C9	0	0	1	0	0	1	0	0	1

(E1,u1) (E2,u2) (E3,u3)

	E1	E2	E3	u1	u2	u3	Df1	Df2	Df3
Re1	1	0	0	1	0	0	1	0	0
Re2	1	0	0	1	0	0	0	1	0
Re3	1	0	0	1	0	0	0	0	1
Re4	0	1	0	0	1	0	1	0	0
Re5	0	1	0	0	1	0	0	1	0
Re6	0	1	0	0	1	0	0	0	1
Re7	0	0	1	0	0	1	1	0	0
Re8	0	0	1	0	0	1	0	1	0
Re9	0	0	1	0	0	1	0	0	1

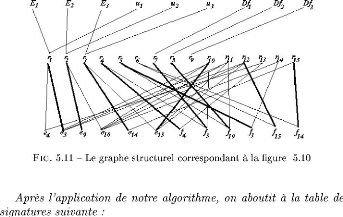
Nous avons commence par la presentation du principe (l'idee de base) de l'algorithme et son application sur le graphe structurel correspondant au systeme physique. A ce niveau, un exemple illustratif de l'algorithme a ete donne.

L'interet du present travail etait de permettre une generation de la table de signatures, directement du modele bond graph, autrement dit sans utilisation d'un modele intermediaire (graphique ou mathematique). Ceci a ete realise via l'adaptation de l'algorithme aux bond graphs couples (systemes complexes). Par consequent, notre contribution est celle de permettre la surveillance des systemes complexes avec les bond graphs couples ( 5.12).

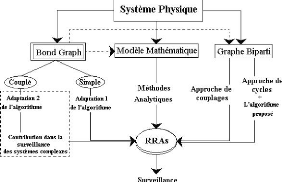
FIG. 5.12 -- Schema qui situe notre contribution en surveillance par les bond graphs

M

M

M*

Symbol's 2000

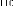
6.0

C

FIG. 5.13 -- Interface de saisie du modele bond graph

0 1 TF GY

R

I C

I C

R

C

C

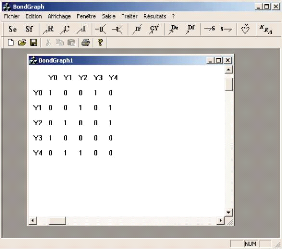
FIG. 5.14 -- Interface d'affichage de la matrice des cycles

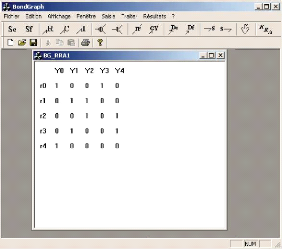
FIG. 5.15 -- Interface d'affichage de la table de signatures