Bond graphs couplés pour la surveillance

1.6 Conclusion

L'objectif de ce chapitre etait de donner un apercu sur les techniques habituelles utilisees pour resoudre les problematiques de la surveillance.

Nous avons commence par une presentation des definitions des mots cies de la surveillance industrielle. Cette derniere se base sur la detection et le diagnostic. La detection permet de signaler toute situation autre qu'une situation normale, dice anormale, suivie par la fonction diagnostic qui va localiser le composant defaillant du systeme et identifier la ou les causes avant provoque cette defaillance.

Pour resoudre le probleme d'ambiguIte pose entre surveillance et supervision, nous avons essaye de decrire la position fonctionnelle et architecturale de chacun des deux dispositifs, permettant ainsi de specifier le role de chacun dans la siirete d'un procede industrial.

Le classement des techniques de surveillance s'effectue en fonction de l'existence ou non d'un modele formel (correspondant au systeme

physique). Nous avons presente comme methodes avec modele, la redondance physique, la redondance analytique et l'estimation parametrique. Et pour les methodes sans modele , nous avons deux categories : la surveillance avec outils statistiques et la surveillance avec reconnaissance des formes, dont chacune comprend plus d'une technique.

La procedure de detection et de localisation des defaillances (FDI), est une procedure qui est citee generalement dans les cas de surveillance avec modele. Les etapes fondamentales de cette derniere ont ete donnees, avec integration des differentes hypotheses connues en matiere de surveillance.

FDI

m1f m2f

m1 m2 m1f - m2f

m1 m2

r1 = m1f - m2f

r2 = m1f - m3f

r3 = m2f - m3f

soient ou non de meme nature. Cette methode (voir chapitre precedent) ne peut etre appliquk qu'en se basant sur un modele formel statique ou dynamique, lineaire ou non lineaire, deterministe ou stochastique du systeme industrial.

2.3 La redondance analytique

La redondance analytique permet une exploitation optimale des informations structurelles du systeme physique. C'est une technique bask sur une redondance implicite au niveau des mesures des grandeurs. La disponibilite d'un modele formel est une condition necessaire pour l'utilisation de cette technique. Il faut prkiser que l'approche analytique ne va pas remplacer l'approche physique, mais elle constitue un complement de cette derniere [32](voir figure 2.3). Par consequent, la redondance analytique permet de :

augmenter l'ordre de redondance,

augmenter la fiabilite et la siirete du systeme de surveillance, remplacer un capteur materiel par un capteur mathematique ou informationnel,

implanter un voteur pour un systeme duplex (redondance physique double), comme illustre sur la figure 2.3.

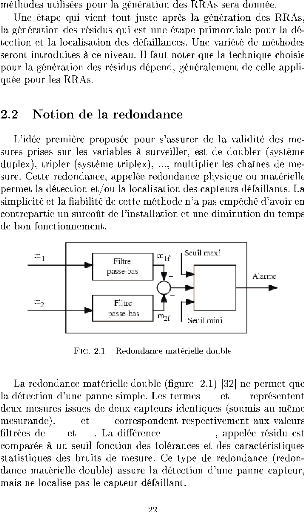
FIG. 2.3 -- Redondance materielle et analytique

La redondance analytique est une technique qui repose sur les actions de cause a effet statiques ou dynamiques entre les entrées et les sorties du systeme physique. Cela permet de surpasser la detection des defaillances capteurs et le passage vers la detection des defaillances produites des actionneurs ou du procede lui meme. Ceci

F Fk

F' F

Vf E F',Vx E X,S(f,x) = 0 Fk

f1(x1,y1) = 0 f2(x2, y2) = 0 f3(y1, y2, y3) = 0

		x1		x2		y1		y2	y3
f1
f2
f3

f3 y1y2 y3

F_x

Fk F F_x = F -- Fk

	y1	y2	x	X -- {x}
f1
f2

x

x

f1 f2

f1(y1,x) = 0
f2(y2,x) = 0

x

x = f-1

1 (y1)

x = f-1

2 (y2)

_f-1

1 (y1) -- f-1

2 (y2) = 0

k

yk xk fk ek

C
F

yk = Cxk + ek + Ffk

x ? IRⁿ y ? IR^m f ? IR^p e ? IR^m C ? IR^m.n F ? IR^m.p

pk

yk

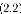
pk = Wyk

W q.m

WC = 0

pk = Wek + WFfk

pk

yk

fk = 0 pk

Wyk = 0

~yk = Cxk + ek + F fk Axk = 0

( ₁ ~ ( _C ~ ( ₁ ~ ( _F ~

yk = xk + ek + fk

0 A 0 0

( C xk ~

W W = 0

A

p

( ₁ )

pk = W yk

0

( ₁ ) ( _F )

pk = W ek + W fk

0 0

( _I )

xk = xk2

_A^-1

1 A2

xk

( _I ~

yk = C xk2 + ek + F fk

_A^-1

1

( _yk )

(I _ C) = ek + F fk
xk

A A1 A

((A1A2)

~

xk1

xk2

A1

Mzk = bk

xk+1 = Axk + Buk + F1fk yk = Cxk + Duk + F2fk

C
CA

?
????

?
????

?
????

?
????

?
????

?
????

?
????

?
????

+ H2

=

CA^s

fk -- s

fk-s+1

fk

uk-s
uk-s+1

uk

xk-s

yk -- s + 1

yk

xk-s + H1

?
????????

H1 =

D 0

CB D

CAB CB

CA^8-1B CA^8-2

H1 H2

F2 ? CF1 CAR1 H1 = ???????? CA^8^-1F1

0 F2 CF1 CA^8^-2F1

0 0 F2 CA^8^-3F1

· · · · · · · · · · · · · · · · · ·

0 0 0 0 0 CF1

0 0 ? 0 ???????? 0 0 F2

x E IR^Th

u E IR^r B

y E IR^m

f E IR F1 F2

s

C
CA

?
????

xk-s + H2

?fk-s

fk-s+1 ? ? ? ?

fk

=

- H1

?
????

CA^s

?
????

?
????

?
????

? ?

yk-s
? ? yk-s+1 ? ?

? ?

? ?

yk

uk-s
uk-s+1

uk

0	· ·	·	0		0 ?	0
· ·	·	0	0		D
· · · ·	· ·	0 0	0 0 ????????
· ·	·	0	0		CA^8^-3
· ·	·	CB	D

pk = (W1(z)F1 + W2(z)F2)fk

pk = --(W1(z)B + W2(z)D)uk + W2(z)yk

?
????

? ?

? ?

? ?

? ?

? ?

?
????

T

- H1

rk = w

uk-s
uk-s+1

uk

= _wT _H2

_?fk-s

_fkfk -s+1

? ? ?

yk-s

? _?yk-s+1 ?

? ? ?

? ? ?

? ? ?

yk

W^T

?

?

_wT ? ?

CA^s

A
CA

?
? ? ?

= 0

xk

rk

s

( A -- zI

C ) xk +

F2 ) ^{k =}--D I ) yk )

W(z) = W1(z) + W2(z)

W(z) (A -- zI

C ) = 0

pk

fk

W(z)

( A - zI F _ )

1

W (z) = = 0

C F _ 2

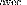
? ? Y ( -I H1 O ) ? U ? = H2f xk_s

? ?

yk-s
? yk - s + 1 ?

? ?

? ?

? ?

yk

et O =

uk-s
uk-s+1

uk

C
CA

CA^s

y =

?
????

?
????

U=

_?fk-s

fk-s+1 ? ? ? ?

fk

? ???? ? ????

f =

? ????

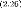
fi = E

j

c_j ...x^aj,p

aj,1 _pkbj,1

1 ...kbj,q

p

cj E IR aj,k, bj,k E IN

F = f1, ..., f_m
X = x1, ..., x_p
K = k1, ..., k_q

F

fi

K

R[x1
·
·
· x_p, k1
·
·
· kq] fi

f f = á1f1 + á2f2 +
·
·
· +

ámfm ái E IR

?(u, y) = 0 u y

(f1,
·
·
· , fm)

X

fi(x1, ...,x_p, k1, ..., k_q) = 0

x1
·
·
· x_p k1
·
·
· k_q

IR R[x1
·
·
· x_p, k1
·
·
· k_q]

f1
·
·
· f_m E

ri = yui - yui

i ? K K

K = {1, 2, · · · }

ri ime

yui ime

cyui ime

ri 0

|ri| > ki > 0 ki ? IR

yu è cyu

yu

ryu = yu-

yu

u(t) f(t)

y(s) = G_u(s)u(s) + Gf(s)f(s)

?(u,y) = r

(yui) ( cyui)

H_u(s) H_y(s)

r(s) = H_u(s)u(s) + H_y(s)y(s)

y(s)

r(s) = (H_u(s) + H_y(s)G_u(s))u(s) + H_y(s)Gf(s)f(s)

y

è

è y

H_u(s) H_y(s)

H_u(s) + H_y(s)G_u(s) = 0

y ènom

r_y = y -- y y rè = ènom

r_y

rè

è

r(t) = (r1(t)r2(t) · · · r_p(t))^T r(t) E IR^p

p

{ 1 si |ri(t)| = ki ei(t) = 0 si |ri(t)| < ki

e(t) = (e1(t)e2(t) · · · ep(t))T

e(t)

i ? p ki

t ri(t)

ki

Ö

í(t) = (í1(t)í1(t) · · · ík(t))^T

r ? - - Öí

ime Ö

Öi = _eíi eíi e ime

Ö p × k

0 1 ? --

r ? - - 0

r

ri(t)

íi(t) k

p p = k = 3

_ime

_ime

?

^r = ?

? ? ? ? ? r1 í1 1 0 0 r2 ? ? - - ? í2 ? = ?0 1 0 ? r3 í3 0 0 1

? ?

í1 í2 í3

? ?

Se. _{z } |._soo. }

Ö í

0

1

p1	p2	p3	p4	Re1
1	1	0	0	Re2
1	1	1	0	Re3
1	1	0	1	Re4
0	0	1	1

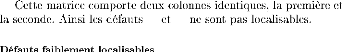
p1 p2

p1	p2	p3	p4	Re1
1	1	0	0	Re2
1	0	1	0	Re3
1	1	0	0	Re4
0	0	1	1

	p1	p2	p3		p4	Re1
1	1	0	0		Re2
1	0	1	0		Re3
0	1	0	1		Re4
0	0	1	1

p1	p2	p3	p4	Re1
0	1	1	1	Re2
1	0	1	1	Re3
1	1	0	1	Re4
1	1	1	0

40

Umi=1 Ci fi

zj,j = {1,...,n}

fi(z1, ...,zp) = 0 1 = p = n

Z = {z1, ..., z_n}

F = {f1, ..., f_m}

Z

				u(t)
			d(t)
			ä(t)
			x(t)
			y(t)
			å(t)
			è

F = {f1, f2, f3, f4, f5, f6,f7,f8,f9, f10, f11} K = {c1,c2, c3, c4, c5}

Z Z = X ? K X

K

F

K

K = U ? P ? Y U P Y

X = {x1, x2, x3, x4, x5, x6, x7, x8, x9, x10}

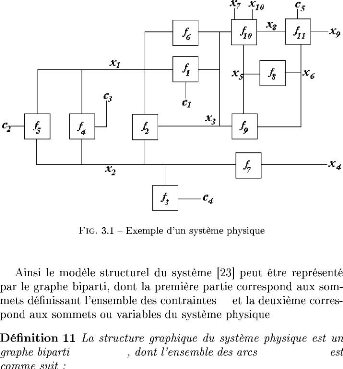
F

Z

G(F, Z, A) A c (F x Z)

? ?

?

A :FxX-->10,11

A* :XxF-->10,11
KF :FxK-->10,11

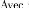
~ 0 si fi s'applique sur xj

(fi, xj) = aij E A, aij =

1 sinon

~ 0 si xi est calculable en utilisant xj

(xi, fj) = a* ij E A, a^*ij =

1 sinon

~ 0 si fi s'applique sur kj

=

(fi,kj) = kifj E A,kifj

1 sinon

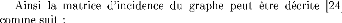
Z

K	F	X	K
0	KF	0	F
KF^T	0	A	X
0	A^*	0

c1

c2

c3

c4

c5

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

f1

f2

f3

f4

f5

f6

f7

f8

f9

f10

f11

(F, Q(F))
F F_x Q(F) = Qk(F) U

Q_x(f) Qk(f) Q_x(f)

F(Qk(F),Q_x(F))

Q_x(F)

Qk(F)

Card_sol(F, Q(F))

(F, Q(F))

(F, Q(F))

Qk(F)

(F, Q(F))

?ö c F Ö = F Q_x(Ö) = Q_x(F)

Qk(F) Qx(Ö)

ö Q_x(F)

Card_sol(F, Q(F)) = 1

(F, Q(F))

Q_x(Ö) = Q_x(F)

(F, Qx(F),Qk(F)) Q_x(F)

(F, Q(F))

(F, Q(F)) Qk(F)

Q_x(F) F
Card_sol(F, Q(F)) > 1

Q_x(F) F

Card_sol(F, Q(F)) =6 ⁰

F

G+

G(X,U) K ? U

K

i ? X

K ? U K i

Qk(F) F

(F, Q_x(F), Qk(F))

Q_x(F)

Qk(F) F

(F, Q_x(F), Qk(F))

Q_x(F)

Qk(F)

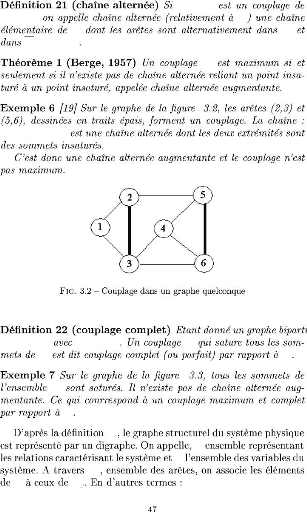
F A_z

K ? U

G(X,U) K

G K

L = {1,2,3,4}

G(X,Y, U) |X| = |Y | K

X X

K = U - K

X

X

A_z

10

Z

F

K

(f, z) E A_z ? S(f, z) = 1 G(FX, X, AX)

a = (FX(a),X(a))

FX(a) X(a)

AXC c AX

Va1, a2 E _AXC a1 =6 a2 ? FXC(a1) ⁼⁶ FXC(a2) A XC(a1) =6 XC(a2)

G+ = (F ⁺,X⁺,A⁺) Q(F +) = X+

X+ F +

G(FX_C, XC, AXC)

G(FX,X,AX) _FXC c FX XC c X

G(FX, X, AX)

G= = (F ⁼,X⁼,A⁼) Q(F ⁼)X⁼ nX⁺

_X= _F=

G- = (F ^-,X^-,A^-)

_F- X-

_G+

|F +| > |X⁺|

_X+

G+

x

_X+

F +

x _G= _G-

x1 x2

x1 x2

Knew = K U {x1, x2}

f1 f2

K

x3 x4

f3 f4

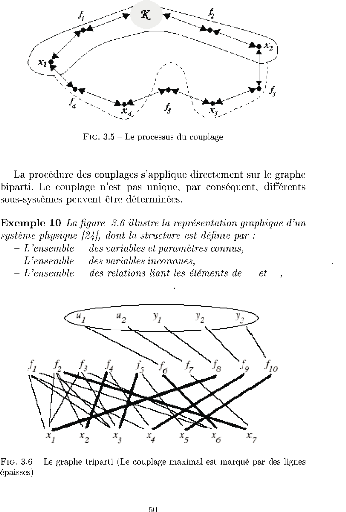
K K = {u1,u2,y1,y2,y3}

X X = {x1,x2,x3,x4,x5,x6,x7}

R K XR =

{f1, f2, f3,f4,f5,f6,f7,f8,f9, f10}

y2 - f9 = x4 - f4 = x2 - f2 = x7 - f7 = u2 y1 - f8 = x1 - f2 = x7 - f7 - u2

y3 - f10 - = x5 - f5 - = x3 - f2 - = x7 - f7 - u2

	u1	u2	y1	y2		y3	Re1
0	1	0	1	0		Re2
0	1	1	0	0		Re3
0	1	0	0	1

u1

u1

u2

u2

u1

u2

G(Fx, X, Ax)

a

(a, 3)

a ? Fx ? 3 ? X Ax n (a, 3) = ö a 3

Fx 3 X

x

G(Fx, X, Ax)

G(Fx, X, Ax)

dim(G(Fx, X, Ax)) = min(a,$)?X (|a| + |3|)

G(FX, X, AX)

(á_*, â^*)

(á^*, â_*) (á, â)

á_* ? á á_* = ö

á ? á*

â_* ? â â_* = ö â ? â*

G(FX, X, AX)

B+ = G(á^*, â_*, A⁺_X) B- = G(á_*, â^*, A⁺_X) B0 = G(á^* \ á*, â^* \ â_*, A⁰_X)

á* = {f1, ..., fk} â_* = {x1, ..., xl} ? k > l

â*

_á*

(á^*, â_*)

G(FX, X, AX)

(á^*, â_*)

A⁺_X = AX n (á^*.â_*)

A^-_X = AX n (á_*.â^*)

A⁰_X = AX n (á^* \ á_*,â^* \ â_*)

(á^*\á_*, â^*\â_*)

â_*

á* \ á_* = {fk+1, ..., fk+p} â* \ â_* = {xl+1,...,xl+p}

â* \ â*

á* \ á_*

á* \ á_*

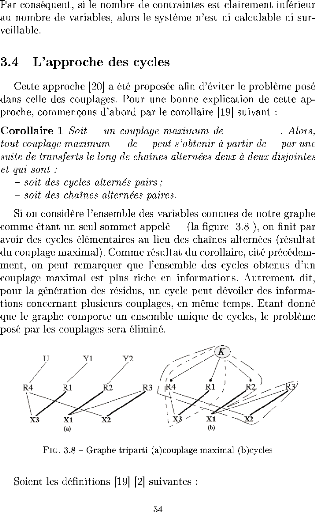
C G = [X,U]

C' G C

K

á_* = {fk+p+1, ..., fm} â^* = {xl+p+1, ..., x_n} ? m - k < n - l

K = {U,Y1,Y2}

C1 : u1 -- f6^--f3^--x3^--f5^--x5^--f10^--y3

C2 : u1 -- f6 -- x6 -- f1 -- x1 -- f8 -- y1

C3 : u2--f7--x7--f2--x2--f4--x4--f9--y2

C4 : y2--f9--x4--f1--x1--f8--y1

C5 : y2--f9--x4--f1--x3--f5--x5--f10--y3

{i0,i1,...,i_q}

C6 : y2 - f9 - x4 - f1 - x6 - f6 - u1

C7 : y3 - f9 - x4 - f4 - x2 - f2 - x3 - f5 - x5 - f10 - u2

C8 : y1 - f8 - x1 - f2 - x3 - f7 - u2

C9 : y3 - f10 - x5 - f5 - x3 - f2 - x7 - f7 - u2

	u1	u2	y1	y2		y3	Re1
0	1	0	1	0		Re2
1	0	0	0	1		Re3
1	0	1	0	0		Re4
0	0	1	1	0		Re5
0	0	0	1	1		Re6
1	0	0	1	1		Re7
0	0	0	1	1		Re8
0	1	1	0	0		Re9
0	0	0	1	1