Modélisation d'une centrale hydroélectrique (cas de la centrale de Mwadingusha)

2.3. Modèle d'état d'un système

2.3.1. Variables d'état

Qualitativement, l'état d'un système se réfère au comportement initial, courant et futur d'un système.

Quantitativement, il est défini par un ensemble minimum des variables notées X₁(t₀), X₂(t₁), ..., X_n(t_n) qui sont spécifiées à l'instant t = t_i et qui, ensemble avec les entrées données U₁(t₁), U₂(t₂), ...,U_n(t_n) pour t=0 déterminent l'état pour n'importe quel instant futur t > t₀.

Les variables appelées variables d'état, X_i(t) définit un ensemble minimum des variables qui déterminent l'état d'un système ; ils sont des informations minimales pour pouvoir décrire les comportements futurs. L'ensemble de ces variables constituent les composantes d'un vecteur appelé vecteur d'état du système.

Ainsi le vecteur d'état est un vecteur qui décrit le comportement dynamique du système en termes de n variables.

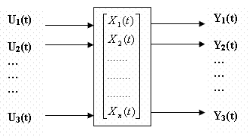
Figure I.2. Vecteur d'état d'un système dynamique

2.3.2. Modèle d'état d'un système

Etant donné que la dynamique d'un système est complètement définit pour vecteur d'état. Ce système peut être alors modélisé par le modèle d'état dont les équations sont données par :

Où :

U(t) : Vecteur d'entrée ou vecteur de commande

Y(t) : la sortie réglée du système

A : matrice dynamique du système

B : matrice de commande du système

C : matrice d'observation

D : matrice de liaison directe

Généralement, il n'y a pas liaison directe entre la variable de commande et la sortie réglée et le modèle se réduit à :

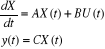
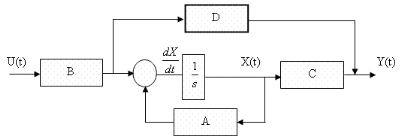
Figure I.3. Diagramme en bloc de la modélisation d'Etat d'un système ).

2.3.3. Contrôlabilité et Observabilité

2.3.3.1. Contrôlabilité

Les problématiques générales de l'automatisme consistent à commander et à contrôler un système de manière à ce qu'il évolue depuis un état initial vers un état final déterminé.

En représentation d'état, il s'agira de déterminer le signal de commande U(t) entre deux états donnés t₁ et t₂ pour ramener le système de l'état X(t₁) vers un état X(t₂).

Critère de Kalman

Un système est complètement accessible, commandable ou contrôlable si et seulement si les vecteurs sont linéairement indépendants ou si la matrice de commande Q définit par est de rang n.

2.3.3.2. Observabilité.

Des nombreuses méthodes de commande de processus utilisent le principe de retour d'état. Comme dans la plus part des cas, les seules grandeurs accessibles du système sont les variables d'entrée et de sortie.

Il est nécessaire, à partir des ces informations de construire l'état du modèle choisi pour élaborer la commande. Un reconstructeur d'état ou estimateur est un système ayant comme entrées, les entrées et sorties du système réel et dont la sortie est une estimation de l'état de ce système.

En plus, certaines variables d'état sont très faciles à mesurer et les autres sont non mesurables. Les variables non mesurables peuvent, comme celles mesurables influencer la sortie y(t) du système. Il est donc possible à partir de la mesure de la sortie de déduire les grandeurs considérées.

Un système est donc observable à un instant t₁ si la connaissance du signal d'entrée et du signal de sortie sur un intervalle de temps [t₁, t₂] permet de calculer l'état du système à l'instant t_1.

a) Critère d'observabilité

Un système est complètement observable si et seulement si les vecteurs lignes où n est l'ordre de la matrice A, sont linéairement indépendants, ou si la matrice colonne d'observabilité N est de rang n.

b) Reconstructeur d'état

Sous l'hypothèse de linéarité du modèle du processus, la structure de base de l'estimateur est toujours la même, mais sa réalisation dépendra du contexte choisit : continu ou discret, déterministe ou stochastique.

Dans le cas où ce modèle est déterministe, le reconstructeur d'état est appelé observateur.

Dans le cas des systèmes bruité, où intervient de phénomène aléatoire, on parle de filtres.

1°) Principe des observateurs

Soit un système continu décrit par l'équation d'état (déterministe non bruité) :

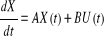
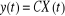
Comme l'état n'est pas généralement accessible, l'objectif d'un observateur consiste en vue de réaliser une commande par retour d'état, d'estimer cet état par une variable notée. Cette estimation est réalisée par un système dynamique dont la sortie est précisément et l'entrée sera constituée de U(t) et y(t). La structure de l'observateur est de la forme :

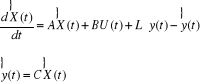
Où L est le gain de l'observateur.

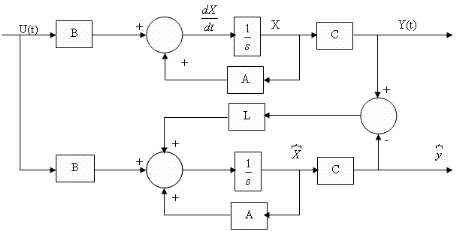
Figure I.4. Diagramme en bloc d'un estimateur d'état d'un système