Modélisation d'une centrale hydroélectrique (cas de la centrale de Mwadingusha)

2°) Observateur prédicteur ou correcteur.

Considérons le système discret stationnaire défini par :

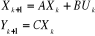
Où k appartient à N, est l'état du modèle, U_k est l'entrée du processus et y_k est la sortie du processus.

A, B, C sont les matrices définies par le modèle d'état.

Soit un observateur pour ce système dont le principe est le même que dans le cas des systèmes continu.

Où G_k est le terme de correction.

a) PREDICTEUR

Pour un prédicteur, on envisage où L_p est le gain du prédicteur, ce qui conduit au constructeur d'état définit par :

Ce qui peut s'écrire également :

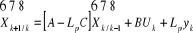
Cette structure est identique à celle définie dans le cas des systèmes continus. En notant l'erreur de reconstruction, il convient :

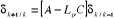
Le reconstructeur est asymptotique si le gain L_p est choisit de sorte que les valeurs propres de la matrice A- L_pC sont, en module, inférieurs à l'unité.

b) LE CORRECTEUR

Dans le cas où y_k+1 est connue, on peut envisager que où L_c est un gain et représente l'estimation de la sortie à l'instant k+1 qui peut être réalisée de deux façons différentes : par anticipation ou par prédiction.

L'estimation de X_k+1 est fournie par le reconstructeur :

Anticipation : si on suppose connue_, on se pose dans le cas : ce qui conduit à écrire l'observateur sous la forme :

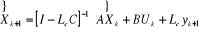
L'erreur de reconstruction est définit par l'équation récurrente :

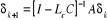
Le reconstructeur est asymptotique si le gain L_c est choisit de telle sorte que la matrice ait les valeurs propres dont le module est inférieur à l'unité.

Prédiction : dans ce cas, y_k+1 est la meilleure estimation que l'on puisse faire de la sortie à partir de l'information disponible avant le calcul de, on pose donc :

Ce qui conduit à la deuxième forme du reconstructeur - correcteur.

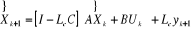
Dans ce cas, l'erreur du reconstructeur devient :

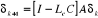
Signalons cependant que dans le cas des systèmes discrets, il existe un choix particulièrement intéressant qui consiste à déterminer L tel que la matrice soit nilpotente, c'est-à-dire que toutes les valeurs propres soient nulles.

3°) OBSERVATEUR DETECTEUR DES DEFAUTS

Outre la reconstruction de l'état pour élaborer une commande par retour d'état, une autre application importante des observateurs est celle utilisée en diagnostic et détection.

Dans cette optique on utilise l'observateur pour générer des résidus permettant d'élaborer une décision dans un étage de surveillance (supervision) et diagnostic du système lorsque les perturbations ou des défauts apparaissent sur un processus. On a en effet des variables qui agissent sur le système mais qui ne peuvent être mesurée et l'objectif consiste ici à construire des résidus qui doivent être sensibles aux défauts du système et en plus doivent permettre de les retrouver et dans ce cas on parle de l'isolation des défauts.

Considérons le modèle :

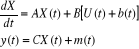
Où b(t) représente une défaillance des actionneurs,

m(t) : défaillance des capteurs

L'utilisation d'un observateur donné par :

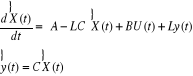
Conduit au résidu :

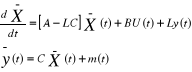
Si L est telle soit une matrice de Hurwitz, le résidu tend bien vers O en l'absence de défauts. Le transfert entre défauts et le résidu s'écrit :

Ce qui, en tenant compte du lemme d'inversion, se met sous la forme :

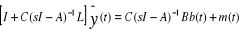
A partir de cette relation, on peut construire :

Ø En l'absence de défauts actionneurs, le système permettant d'isoler les défauts capteurs à partir des résidus :

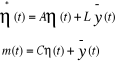
Ø En l'absence de défauts capteurs, le système permettant d'isoler les défauts actionneurs à partir des résidus et construit à partir de la variable î(t) définit par :

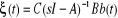
Cette variable est estimée à partir du système :

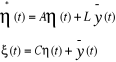
Et l'estimation d'une défaillance capteur est donnée par l'inversion du système initial à savoir :

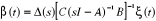
Où est la matrice du filtre tel que soit bicausale.

Â(t) n'est pas une estimation des défauts mais plutôt un filtre de défauts, cependant le caractère diagonal de permet l'isolation de défauts.

Dans le cadre de notre travail, un observateur détecteur de défauts est d'une grande importance pour la supervision des boucles de régulations dont les défauts peuvent affecter soit l'actionneur, soit le capteur ou l'organe de mesure ou soit encore le processus lui-même.