Les pompe solaires : Dimensionnement d'une station de pompage en zone maraîcher

Figure 2.3 Abaques

On pourra utiliser en première approximation les valeurs données ci-dessous :

· pour un coude à 90°, arrondis à section circulaire, carré ou rectangulaire à grand coté perpendiculaire au rayon de courbure

		0,5	0,75	1	1,5	2
	z	1	0,45	0,30	0,20	0,20

· pour un coude à 90°, arrondis à section rectangulaire à grand coté suivant le rayon de courbure

	R/d	0,5	0,75	1	1,5	2
	z	1,5	0,7	0,45	0,3	0,3

·  pour un coude à 90°, brusque,

avec arrondi extérieur z = 1

sans arrondi extérieur z = 1,5

· élargissement brusque, en ligne droite

z 1 rapporté à la vitesse dans S1 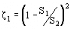sortie de conduit z 1=1 (S2 = 8)

· rétrécissement brusque, en ligne droite

z 2 rapporté à la vitesse dans S2 z 2 =0,5 entrée de conduit z2=0,5

ABAQUE DES PERTES DE CHARGES

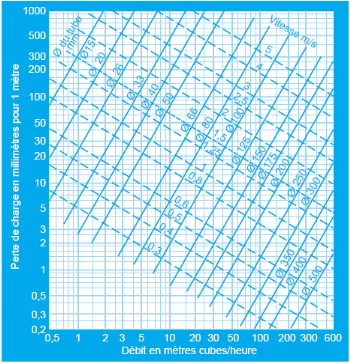
Figure 2.4 abaques les pertes de charges connaissant le débit

Pour différentes valeurs des pertes de charges, nous adopterons pour simplifier les calculs l'utilisation de ce tableau de valeurs.

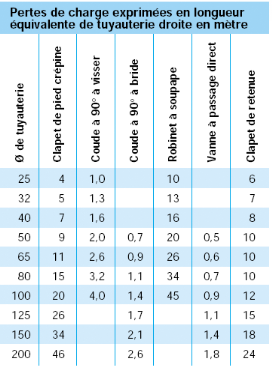
Figure 2.5 Pertes de quelques éléments hydrauliques

Viscosité de l'eau :

Dans de nombreuses formules apparaît le rapport de la viscosité 
dynamique h et de la masse volumique r 
Ce rapport est appelé viscosité cinématique  

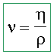
Dimension : [n ] = L² T^-1  
unité SI  : m²/s        système cgs :le Stock (St) 1m²/s = 10⁶ cSt 

La valeur de la viscosité est fonction de la température qui influe beaucoup sur l'état du fluide. Ce tableau représente les profils de la viscosité en fonction de la température d'utilisation.

Tableau 2.4 Viscosité en fonction de la température

Temp °C	Viscosité cinématique (x 10^-6)
°C	m^2/s
5	1,520
10	1,308
11	1,275
12	1,241
13	1,208
14	1,174
15	1,141
16	1,115
17	1,088
18	1,061
19	1,034
20	1,005
21	0,985
22	0,963
23	0,941
24	0,919
25	0,896
26	0,878
27	0,856
28	0,841
29	0,823
30	0,804
35	0,727
40	0,661
50	0,556
65	0,442

Par ailleurs le poids volumique de l'eau

ñ*g= ã

pour l'eau : ã = 9.81 KN/m³

le graphe ci-dessous montre son évolution en fonction de la température pour une plage de données.

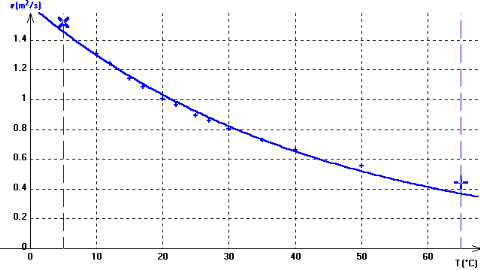
Figure 2.6 Viscosité en fonction de la température