Application des générateurs de scénarios économiques en alm pour les compagnies d'assurance

65

CHAPITRE 3. LA GESTION ACTIF PASSIF DANS LE CADRE DE L'ASSURANCE

Récolte des dividendes

Les dividendes sont les revenus des actions et elles sont calculés sur la base de la valeur de marché de l'actif.

Dividendest = V Mt * Txdiv (3.7.4)

Stratégie de réinvestissement

Au final, la rentabilité des investissements réalisé se mesure par l'allocation cible fixée au début. Néanmoins dans un contexte d'excès de rachat ou de mortalité l'assureur sera obligé de liquide les titres financiers afin de bien gérer ses risques et d'assurer des projections plus réalistes.

De ce fait on retient le même travail, on re projette de nouveau le panier d'actif à l'aide des générateurs de scénarios économiques et on fixe de nouveau une allocation optimale d'actifs.

On introduit ces outputs de nouveau dans le moteur ALM afin de mieux clarifier les nouveaux risques issus de ce nouveau mécanisme.

66

Chapitre 4

Application pratique de la mise en

place d'un GSE et projection au sein

du modèle ALM

Introduction

Ce chapitre propose l'élaboration d'un Générateur de Scénarios Economiques pour une compagnie d'assurance qui permet de projeter des facteurs de risques économiques et financiers. Ces derniers seront utilisés pour la projection du bilan, du compte de résultat technique (en cas d'assurance non-vie) et l'état de flux de trésorerie (en cas assurance non-vie) .

Pour rappel, ce mémoire est élaborée dans un cadre tunisien² nous avons rencontré certaines difficultés au niveau des études pratiques :

· Insuffisance des données.

· L'instabilité du climat économique et politique.

· Incomplétude de marché financier tunisien due à une économie stationnaire avec de faibles performances.

Néanmoins, nous arrivons à collecter des données historiques à des horizons variables pour calibrer et projeter chaque variable selon le modèle retenu (modèle de référence).

Nous rappelons que dans ce mémoire, le modèle de référence utilisé pour projeter les variables macro-économiques est Ahlgrim et Al. présenté au niveau du chapitre 2.

Dans la section suivante nous allons présenter une analyse des données utilisées dans notre étude.

4.1 Analyse des données

Les facteurs des risques considérés dans notre analyse sont : le taux d'inflation, le taux d'intérêt, le rendement des actions et le rendement immobilier.

Ce choix des variables est efféctué car elles représentent les inputs du modèle de référence

2. Source des données

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

choisi. Ces dernières sont calculées à un pas annuel.

Les différents tests et modélisation statistiques dans la suite ont été réalisés à l'aide du logiciel libre statistique R.

Nous avons utilisé pour ce fait les librairies : Moments, tseries (pour les séries temporelles) et GLM.

Les codes R relatifs à la calibration et la projection du modèle d'Ahlgrim et Al. sont disponibles sur le site Ressources actuarielles [18] .

4.1.1 Taux d'inflation

L'inflation est définie par : "la perte du pouvoir d'achat de la monnaie qui se traduit par une augmentation générale et durable des prix. ... La perte de valeur de la monnaie est un phénomène qui frappe l'économie nationale dans son ensemble (ménages, entreprises, etc."[5] Pour la Tunisie, comme pour d'autres pays, l'inflation se calcule sur la base de l'indice des prix à la consommation (IPC) ¹ base 100 en 2015. Le calcul de l'IPC est donné par:

Prix d^'un panier de biens et de services d^'une année t

IPCt = * 100 (4.1.1)
P rix d'un panier de biens et de services de l'année de base

Ensuite, nous proposons dans le cadre de l'élaboration de ce mémoire une construction de taux d'inflation par la formule suivante :

Inft = ( IP Ct ) - 1 (4.1.2)

IP Ct-1

Pour la modélisation de cette variable nous choisissons un historique de l'IPC de 30 ans entre 1990 et 2021, les données utilisées sont disponibles sur le site de l'institu national de la statistique.

La figure ci-dessous, publié par la banque illustre l'évolution de l'inflation en Tunisie depuis 1990 jusqu'au 2020 en citant les principaux facteurs de déviation de l'inflation :

67

1. L'indice des prix à la consommation est l'instrument de mesure de l'inflation. Il permet d'estimer, entre deux périodes données, la variation moyenne des prix des produits consommés par les ménages. C'est une mesure synthétique de l'évolution de prix des produits, à qualité constante.[13]

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

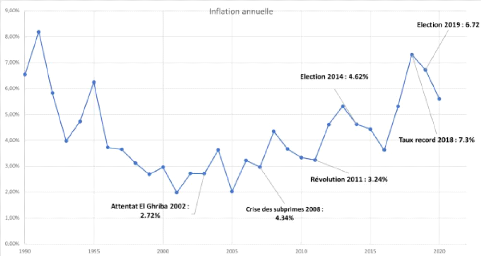
FIGURE 4.1 - Evolution de l'inflation entre 1990-2020 (Source : INS ) [12]

En Tunisie l'inflation garde une évolution en exponentielle depuis l'année 2011 ¹ et atteint un pique de 7.3% en 2018 et se stabilise à 6.2% fin 2020. Ceci est conséquence de l'instabilité économique et politique qui se traduit par l'augmentation du taux de déficit commercial : une vision stratégique doit être prise en compte pour lutter ce phénomène qui menace l'économie. Le tableau (4.1) ci-dessus représente les caractéristiques statistiques de la série des données utilisées :

		Taux d'inflation entre 1990-2020	Moyenne
0.042		Ecart type
0.015		Médiane
0.037		Maximum
0.082		Minimum
0.010		Skewness
0.725		Kurtosis
2.802		Jarque-Bera
0.0610

TABLE 4.1 - Statistiques du taux d'inflation entre 1990-2021

Les résultats obtenus permettent de conclure que :

· L'hypothèse de normalité est à rejeter (Test de Jarque-Bera).

· Une asymétrie de la distribution empirique de l'échantillon à droite (Skewness et Kurtosis).

Ces données sont utilisées pour le calibrage et la projection du modèle retenu pour le taux d'inflation qu'on détaillera dans la section suivante, nous étudions par la suite les données relatives au Taux d'intérêt.

1. Année de la révolution

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

4.1.2 Taux d'intérêt

Le Taux moyen du marché monétaire ¹ correspond au taux auquel les banques s'empruntent et se prêtent de l'argent entre elles. Il joue un rôle essentiel dans l'activité financière et fluctue en fonction de l'inflation, du chômage, mais aussi de la conjoncture internationale.[4]

Dans le cadre tunisien, le TMM est fixé par la BCT² et varie soit à la hausse soit à la baisse selon le contexte économique. En effet, une baisse de TMM conduit à une hausse des demandes de crédits par les investisseurs avec des coûts non élevés mais un retour sur investissement qui peut être rentable. Cependant, une augmentation de TMM est effectuée afin de limiter et régulariser la demande de crédit et créer une marge d'intérêt plus importante.[11].

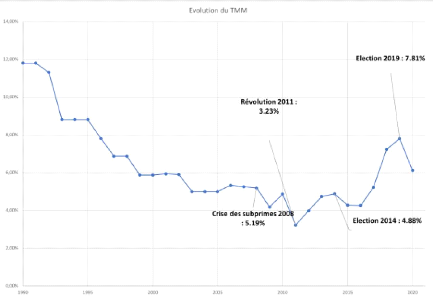
La courbe suivante souligne l'évolution du taux d'intérêt réel durant les 30 dernières années en Tunisie :

FIGURE 4.2 - Evolution du TMM entre 1990-2020 (Source : INS) [23]

Le TMM a passé de 4,11% à 7,24% entre 2011 et 2019, la banque centrale de Tunisie considère que cette augmentation de 3,13% grave sur les budgets et la trésorerie des ménages dans un pays qui connait une hausse des prix en exponentielle.³

Le taux de marché monétaire est un taux nominal déterminé à partir de l'inflation par une intégration. En revanche, pour avoir une vision plus réaliste de ce que rapportera le placement du préteur, ou bien qu'il coutera à l'emprunteur, il est nécessaire de tenir compte de l'inflation et de raisonner en terme de taux réel plutôt qu'en terme de taux nominal. Ainsi la relation qui relie ces taux se traduit par :

1. Abrégé TMM

2. Banque Centrale de la Tunisie

3. Inspiré de la note banque centrale 2019

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Taux réel = Taux nominal - Taux inflation[30]

On distingue entre un taux d'intérêt à court terme et un taux d'intérêt à long terme, en effet :

· Taux d'intérêt à court terme est déterminé à partir du TMM que publie la BCT et en utilisant la relation précédente 29.

· Taux d'intérêt à long terme est celui des obligations d'État à échéance de 10 ans. Les taux dépendent essentiellement du prix facturé par le prêteur, du risque propre à l'emprunteur et de la réduction de la valeur du capital. ... Les taux d'intérêts à long terme sont un déterminant de l'investissement des entreprises.[17]

Nous présenterons dans la suite les statistiques des données collectées sur le taux d'intérêt à long terme et le taux d'intérêt à court terme.

Concernant la modélisation du taux d'intérêt à long terme, nous utilisons un historique de 30 ans entre 1990 et 2020 partagé par la banque centrale.

Les tableaux (4.2) et (4.3) ci-dessus présentent les mêmes caractéristiques statistiques des séries des données utilisées :

		Taux réel à court terme entre 1990-2020	Moyenne
0.194		Ecart type
1.811		Médiane
2.287		Maximum
5.548		Minimum
-0.932		Skewness
0.142		Kurtosis
1.856		Jarque-Bera
1.792

TABLE 4.2 - Statistique du Taux réel à court terme entre 1990-2020

		Taux réel à long terme entre 2007-2020	Moyenne
0.245		Ecart type
0.016		Médiane
0.0663		Maximum
0.103		Minimum
0.051		Skewness
0.672		Kurtosis
2.107		Jarque-Bera
1.629

TABLE 4.3 - Statistique du Taux réel à long terme entre 2007-2021

Les résultats permetent de conclure que :

· L'hypothèse de normalité est à rejeter (Test de Jarque-Bera).

· Une asymétrie de la distribution empirique de l'èchantillon à droite (Skewness et Kurtosis).

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

4.1.3 Rendement des actions

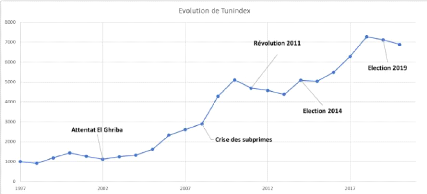
Pour la collecte des historiques des rendements des actions tunisiennes nous nous se focalise sur l'indice boursier Tunindex¹.

Les données sont récupérées à partir de l'institut nationale de la statistique (INS) entre 1997 et 2020[12], le graphique ci-dessous illustre l'évolution de TUNINDEX en tenant compte les principaux facteurs de volatilités au cours de la période d'étude.

FIGURE 4.3 - Evolution de TUNINDEX entre 1997-2020 (Source : INS) [12]

Dans le cadre de ce mémoire la construction de l'historique des rendements de l'action à partir de l'indice boursier Tunindex est donnée par la formule suivante :

Rendaction n = ( ^indn ) - 1 (4.1.3)
indn-1 Où Rendaction

n représente le rendement de l'action et ind_n représente l'indice Tunindex avec
dividendes réinvestis à l'année n.

Le rendement de l'action associé à l'historique du rendement annuel construit entre 1997 et 2020 est présenté dans la figure ci-dessous :

1. L'indice TUNINDEX est un indice boursier tunisien pondéré par les capitalisations boursières flottantes avec une base 1000, C'est un indice statistique, de type rendement (les dividendes sont réinvestis), qui mesureent la tendance générale des marchés des titres de capital de la Cote de la Bourse, composés des cinquantes principales capitalisations boursières du pays.[24]

L'indice des prix immobilier IPM est utilisé pour la projection du rendement de l'immobilier. c'est un indice trimestriel établi dans le cadre d'un projet de suivi des prix de l'immobilier à

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

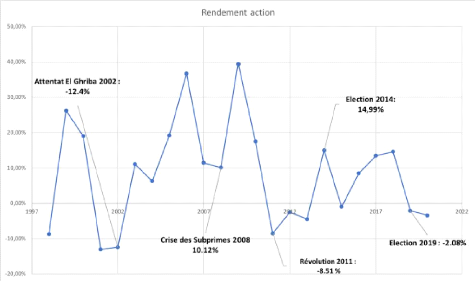
FIGURE 4.4 - Evolution du rendement de l'action entre 1997-2020 (Source : INS) [12]

Le tableau ci-dessous représente les caractéristiques statistiques de la série des données utilisées :

		Rendement de l'action entre 1997-2020	Moyenne
0.093		Ecart type
0.162		Médiane
0.097		Maximum
0.483		Minimum
-0.121		Skewness
0.771		Kurtosis
3.098		Jarque-Bera
2.389

TABLE 4.4 - Statistique du rendement de l'action entre 1997-1990

Les résultats permet de conclure que :

· L'hypothèse de normalité est rejetée (Test de Jarque-Bera).

· Une légère asymétrie de la distribution empirique de l'echantillon à gauche (Skewness).

Ces données sont utilisées pour le calibrage et la projection du modèle retenu pour le rendement de l'action que nous détaillerons dans la section suivante, nous étudions dans la suite les données relatives au rendement de l'immobilier.

4.1.4 Rendement de l'immobilier

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

usage d'habitation au sein de l'institut national de la statistique (INS).

Dans le cadre de ce mémoire et pour simplifier nous considérons que les indices du quatrième trimestre représentent les indices immobiliers annuels.

L'historique du rendement immobilier pour chaque année est construit à partir de la relation suivante:

Im_n = ( IP Mn ) - 1 (4.1.4)

IP Mn-1

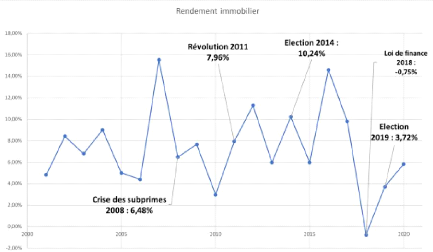
Où IPM_n représente l'indice des prix immobiliers à l'année n. La figure ci-dessous illustre l'évolution du rendement de l'immobilier entre 2000 et 2020 :

FIGURE 4.5 - Evolution du rendement de l'immobilier entre 2000-2020 (Source : INS) [12]

Le tableau ci-dessous représente les caractéristiques statistiques de la série des données utilisées, les résultats réalisés permetent de conclure que :

· L'hypothèse de normalité des données est accepter (Test de Jarque-Bera).

· Une légère asymétrie de la distribution empirique de l'èchantillon à gauche (Skewness).

· Aplatissement proche de celui d'une loi normale centrée réduite (Kurtosis).

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

		Rendement de l'immobilier entre 2000-2020	Moyenne
0.075		Ecart type
0.038		Médiane
0.077		Maximum
0.154		Minimum
-0.012		Skewness
0.044		Kurtosis
3.117		Jarque-Bera
0.730

TABLE 4.5 - Statistique du rendement de l'immobilier entre 2000-2020

4.2 Calibrage des données

Nous proposons dans la suite une calibration des variables macro-économique selon le modèle d'Ahlgrim et Al. ^1.

Le modèle d'Ahlgrim et Al présenté dans le deuxieme chapitre sert à déterminer le rendement des actions en prenant comme inputs le taux d'inflation et le taux d'intérêt réel.

Modèle sur l'inflation

Ahlgrim et Al. modélise le taux d'inflation par un processus d'Orstein-Uhlenbeck.

Dans le cadre de ce mémoire nous adoptons ce modèle pour modéliser le taux d'inflation tunisien.

En se basant sur les données tunisiennes sur l'inflation présentées dans la section précédente, les paramétres obtenues sont résumés dans le tableau suivant :

Paramètre		Valeur	Taux d'inflation moyen :
0.041		Ecart-type de l'erreur :u
0.013		Vitesse de retour à la moyenne : k
0.381

TABLE 4.6 - Ahlgrim : Estimation des paramètres du modèle sur l'inflation

Test		Résultat	R2 corrigé
0.481		Fisher
P = 3,559 e5		Moyenne des résidus
6.089 e^-17		Student(constante)
P = 0.048		Student(variable)
P = 3.57 e-5		Breusch-Godfrey
P = 0.549		ARCH(1)
P = 0.633		Jarque-Bera
P = 0.049

TABLE 4.7 - Ahlgrim : Test d'adéquation du modèle sur l'inflation

Le tableau ci-dessus résume les résultats des différents tests d'adéquation sur le modèle, nous pouvons conclure que :

1. Vois chapitre 2 section modèle d'Ahlgrim et Al pour plus de détails.

1. entre 2000 et 2021

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· Le test d'ajustement permet de conclure que le pouvoir explicatif est de 48.1%.

· Le test de Fisher permet de dire que le modèle est globalement significatif.

· La moyenne des résidus est presque nulle.

· Le couple du test de student (constante,variable) affirme que les paramétres utilisés sont significatifs.

· Le test de Breusch-Godfrey montre l'abscence de l'autocorrélation d'ordre P = 1.

· Le test ARCH(1) montre l'abscence de l'hétéroscédasticité d'ordre q = 1.

· Le test de Jarque-Bera permet de validé la normalité des résidus.

L'ensemble des tests réalisés permettent de valider globalement l'adéquation du modèle d'Orstein-Uhlenbeck pour le taux d'inflation.

Modèle sur l'immobilier

Dans le cas tunisien, l'immobilier joue un rôle central dans les portefeuilles des assureurs tunisiens il permet de freindre les conséquences de l'inflation, vu la rentabilité qu'il procure. Ahlgrim et Al dans ses traveaux modélisent cette varibale par un processus d'orstein-uhlenbeck, nous adoptons cette modélisation dans le cadre de ce mémoire. En se basant sur les données tunisiennes sur l'immobilier ¹ présentées dans la section précédente, les paramétres obtenus sont résumés dans le tableau suivant :

Paramètres		Résultat	Vitesse de retour à la moyenne
0.570		Espérance du taux de rendement de l'immobilier
0.073		Ecart type de l'erreur
0.066

TABLE 4.8 - Ahlgrim : Estimation des paramètres du modèle sur l'immobilier

Paramètres	Résultat			R2 corrigé
0.365			Fisher
P = 0.01			Student (Constante)
P = 0.00001			Student (Variable)
P = 1.41 e -	7		Moyenne des résidus
1.301 e - 18			Breusch-Godfrey
P = 0.520			ARCH (1)
P = 0.289			Jarque-Bera
P = 0.049

TABLE 4.9 - Ahlgrim : Test d'adéquation du modèle sur l'immobilier

Le tableau ci-dessus résume les résultats des différents tests d'adéquation sur le modèle, ceci permet de conclure que :

· Le test d'ajustement permet de conclure que le pouvoir explicatif est de 36%.

· Le test de Fisher permet de dire que le modèle est globalement significatif.

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· La moyenne des résidus, on peut le considére nulles.

· Le couple du test de student (constante,variable) affirme que les paramétres sont significatifs.

· Le test de Breusch-Godfrey montre l'abscence de l'autocorrélation d'ordre P = 1.

· Le test ARCH(1) montre l'abscence de l'hétéroscédasticité d'ordre q = 1.

· Le test de Jarque-Bera permet de validé la normalité des résidus.

L'ensemble de ces tests valident les conditions posées pour la validation du modèle et du calibrage. Nous concluons que la modélisation par le processus d'Orstein uhlenbeck est bien adapté au rendement de l'immobilier.

Modèle sur les taux d'intérêt réel

Concernant le taux d'intérêt réel, il est modélisé sous la probabilité risque historique par le processus de Hull and White à deux facteurs.

A noter que le taux court réel r_r(t) oscille autour du taux long ll(t), soit :

dr_r(t) = u_r[ll(t) - r_r(t)]dt + ó_rdW_r(t) (4.2.1)

dl_r(t) = ur,l[êr(t) - ll(t)]dt + óldWl(t) (4.2.2)

En se basant sur les données tunisiennes sur le taux d'intérêt réel ¹ à long et à court terme présentés dans la section précédente, on obtient les paramètres de besoin qui sont résumés dans le tableau ci-dessous.

Paramètres		Résultat	Vitesse de retour à la moyenne (CT)
0.194		Ecart type de l'erreur (CT)
0.018		Vitesse de retour à la moyenne (LT)
2.454		Taux d'intérêt réel moyen (LT)
0.027		Ecart type de l'erreur (LT)
0.020

TABLE 4.10 - Ahlgrim : Estimation des paramètres du modèle sur le taux d'intérêt réel à long et court terme

1. entre 2007 et 2020

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Le tableau suivant représente les tests statistiques nécessaires pour l'adéquation du modèle de taux d'intérêt réel à long terme :

Test	Résultat			R2 corrigé
-0.0834			Fisher
P = 0.716			Student (Constante)
P = 0.006			Student(Variable)
P = 0.716			Moyenne des résidus
2.271 e^-19			Breusch-Godfrey
P = 0.635			ARCH(1)
P = 0.733			Jarque-Bera
P = 9.295	e^-13

TABLE 4.11 - Ahlgrim : Test d'adéquation du modèle sur le taux d'intérêt réel à long terme

Ceci permet de conclure que :

· Le test d'ajustement permet de conclure que le pouvoir explicatif est de -8%.

· Le test de Fisher permet de dire que le modèle est globalement significatif.

· La moyenne des résidus est presque nulle.

· Le couple du test de student (constante,variable) affirme que les paramétres sont significatifs.

· Le test de Breusch-Godfrey montre l'abscence de l'autocorrélation d'ordre P = 1.

· Le test ARCH(1) montre l'abscence de l'hétéroscédasticité d'ordre q = 1.

· Le test de Jarque-Bera permet de valider la normalité des résidus.

Le tableau suivant représente les tests statistiques nécessaire, pour l'adéquation du modèle de taux d'intérêt réel à court terme :

Test		Résultat	R2 corrigé
0.0078		Fisher
P = 0.321		Student(Variable)
P = 0.322		Moyenne des résidus
-0.0004		Breusch-Godfrey
P = 0.238		ARCH(1)
P = 0.763		Jarque-Bera
P = 0.502

TABLE 4.12 - Ahlgrim : Test d'adéquation du modèle sur le taux d'intérêt réel à court terme

Ceci permet de conclure que :

· Le test d'ajustement permet de conclure que le pouvoir explicatif est de 0.8%.

· Le test de Fisher permet de dire que le modèle est globalement significatif.

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· La moyenne des résidus est presque nulle.

· Le test de student (variable) affirme que les paramétres sont significatifs.

· Le test de Breusch-Godfrey montre l'abscence de l'autocorrélation d'ordre P = 1.

· Le test ARCH(1) montre l'abscence de l'hétéroscédasticité d'ordre q = 1.

· Le test de Jarque-Bera permet de valider la normalité des résidus.

L'ensemble de ces tests montre que le modèle de Hull-White n'est pas parfaitement adapté aux données tunisiennes pour les taux d'intérêt réel à long et à court terme, car les testes de fisher et le test d'ajustement ne sont pas tout à fait validés. Cependant nous retenons ces données vu que les résultats issus de ces deux tests sont proches de zéro.

Modèle sur les actions

La modèlisation de l'excès du rendement actions dans le cadre du modèle d'ahlgrim se base sur le processus de Black et Scholes. En se basant sur les données annuelles tunisienne entre la période de 1997 et 2020 des rendements des actions, on obtien l'excès du rendement de l'action par la formule suivante :

Excès du rendement actions = Rendement actions - TMM

On peut donc déduire les paramètres nécessaires pour alimenter le processus de black and Scholes, soit alors :

Paramètre		Résultat	Excès de rendement moyen
0.037		Ecart type de l'excès des actions
0.148

TABLE 4.13 - Ahlgrim : Estimation des paramètres du modèle sur le rendement d'actions

4.3 Projection

Dans cette section nous présentons les résultats de la projection issue des variables validées dans la section précédente pour le modèle d'Ahlgrim.

La projection est réalisée par la génération de trajectoires en utilisant la formule de discrétisation, nous définissons une structure de dépendance pour effectuer des projections cohérentes. Pour le choix de cette structure nous allons adopter la structure de corrélation linéaire ^1.

Hypothèses de projection

Nous présentons dans cette sous-section les hypothèses de projection pour le modèle Ahlgrim and Al ainsi les paramétres et les valeurs initiales nécessaires pour la projection.

· NS = 10000 : Le nombre de simulations.

· T = 10 ans : La maturité de projection.

· Les quantiles sont présentées à 10 % et à 90 %. On suppose que l'année d'origine de projection est t = 2020.

1. Voir la 3^éme étape de construction d'un GSE 2^éme chapitre pour plus de détail.

1. Matrice ci-dessus

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Matrice de corrélation entre les variables du GSE

Pour la modélisation de la dépendance on se focalise sur la matrice de corrélation. Les résidus suivent une loi normale, la génération des trajectoires revient alors à générer des lois normales corrélées, d'où le recours vers la décomposition de Chlesky.

Nous nous intéressons à une projection annuelle, les matrices de corrélations présentées ci-dessous sont estimées à partir des données à fréquences annuelles dont l'historique des variables du GSE est récupéré entre 2007-2020 pour des raisons d'absence de suffisamment des données sur le taux réel long. La matrice de corrélation est intégrée alors comme un paramètre dans le GSE.

Nous présentons dans la suite les matrices de corrélations pour le modèle de référence Ahlgrim and Al ainsi qu'un backtesting sur les résultats obtenus afin d'effectuer des projections cohérentes dans la suite.

Données	Res_Tx_In	Res_Rdt_Im	Res_Tx_rl	Res_Tx_rc		Res_Rdt_ex	Res_Tx_In
1	-0.025	0.693	-0.132	-0.0026		Res_Rdt_Im
-0.025	1	-0.493	-0.005	0.016		Res_Tx_rl
0.693	-0.493	1	0.051	0.020		Res_Tx_rc
-0.132	-0.005	0.051	1	0.228		Res_Rdt_ex
-0.0026	0.016	0.020	0.228	1

TABLE 4.14 - Ahlgrim and Al : Matrice de corrélation de l'historique des résidus Backtesting sur la matrice de corrélation

Comme la matrice de corrélation de l'historique des résidus est symetrique, définie et positive, d'aprés le théoréme de Cholesky, on peut la décomposer comme le produit d'une matrice triangulaire et de sa transposée, soit :

Données	Res_Tx_In	Res_Rdt_Im	Res_Tx_rl	Res_Tx_rc		Res_Rdt_ex	Res_Tx_In
1	0	0	0	0		Res_Rdt_Im
-0.0258	0.999	0	0	0		Res_Tx_rl
0.693	-0.475	0.541	0	0		Res_Tx_rc
-0.132	-0.008	0.257	0.957	0		Res_Rdt_ex
-0.0026	0.015	0.054	0.22	0.973

TABLE 4.15 - Ahlgrim and Al : Matrice de corrélation - Décomposition de Cholesky

Nous proposons une mesure de qualité pour notre GSE de référence Ahlgrim et Al. sur la matrice de corrélations : nous comparons la matrice de corrélations issue des données historiques ¹ avec celle projetée pour vérifier si la structure de dépendance est conservée ou pas. La matrice projetée est présentée ci-dessous.

FIGURE 4.7 - Boostrap : projection de l'inflation

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Données	Inflation	Immobilier	Tx long	Tx court		Excès_action	Inflation
1	-0.023	0.670	-0.127	0.008		Immobilier
-0.023	1	-0.471	-0.004	0.019		Tx long
0.670	-0.471	1	0.043	0.0208		Tx court
-0.127	-0.004	0.043	1	0.221		Excès_action
0.008	0.019	0.0208	0.221	1

TABLE 4.16 - Ahlgrim and Al : Matrice de corrélation projeté

Les valeurs des deux matrices sont très proches donc la structure de dépendance est conservée.

4.3.1 Projection issues du calibrage du modèle d'Ahlgrim et Boos-trap

Nous restreindrons dans cette partie seulement pour présenter les schémas issus du code R

lors de la projection. Voici ci-dessous la chronique des rendements de l'inflation issus du modèle Ahlgrim et Al :

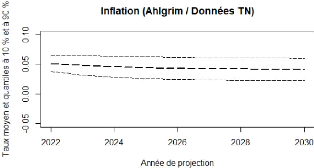
FIGURE 4.6 - Ahlgrim et Al. : projection de l'inflation

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Vous trouvez ci-dessous l'évolution de l'action à long terme des rendements de l'action issus du modèle Ahlgrim et Al et boostrap :

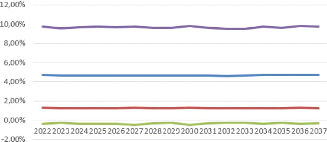
FIGURE 4.8 - Ahlgrim et Al. : projection de l'éxcedent de rendement de l'action

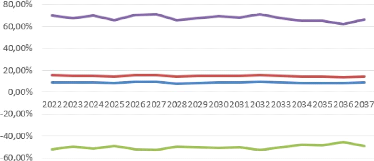
FIGURE 4.9 - Boostrap : projection de l'éxcedent de rendement de l'action

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

Ci-dessous la chronique de l'immobilier issus du modèle Ahlgrim et Al et boostrap :

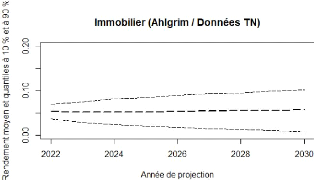
FIGURE 4.10 - Ahlgrim et Al. : projection de l'immobilier

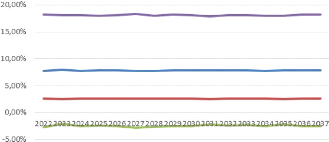
FIGURE 4.11 - Boostrap : projection de l'immobilier

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

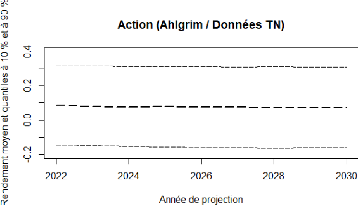
FIGURE 4.12 - Ahlgrim et Al. : projection de rendement de l'action

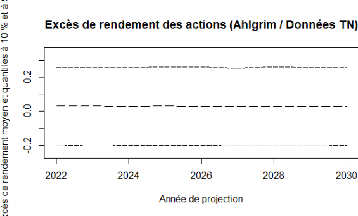
FIGURE 4.13 - Ahlgrim et Al. : projection de Taux court

Vous trouvez ci-dessous la chronique des taux à court et à long terme ainsi la projection des zéro coupon issus du modèle d'Ahlgrim et Al :

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

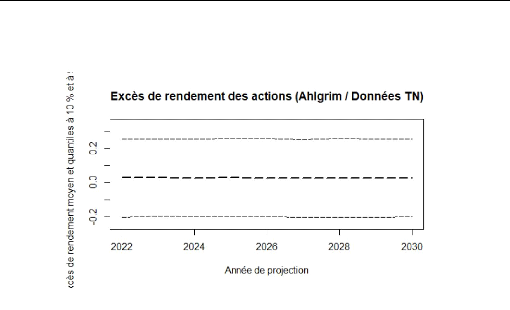
FIGURE 4.14 - Ahlgrim et Al. : projection de Taux court

FIGURE 4.15 - Boostrap : projection de Taux court

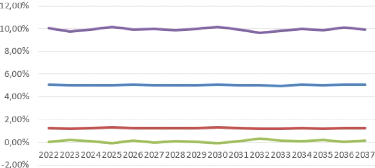
CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

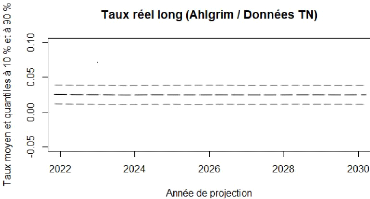
FIGURE 4.16 - Ahlgrim et Al. : projection de Taux long

FIGURE 4.17 - Boostrap : projection de Taux long

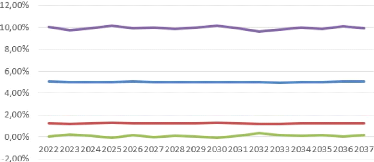
CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

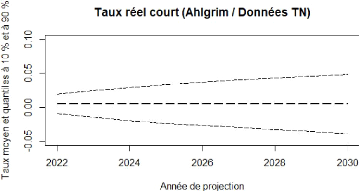
FIGURE 4.18 - Ahlgrim et Al. : projection de taux réel court

FIGURE 4.19 - Boostrap : projection de taux réel court

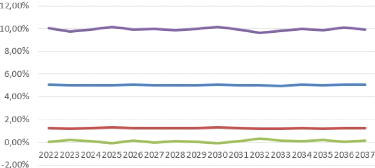
CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

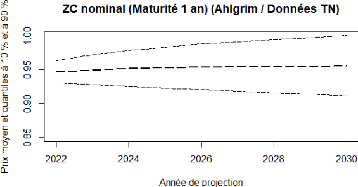
FIGURE 4.20 - Ahlgrim et Al. : projection de Zero coupon nominal

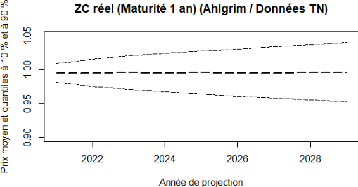
FIGURE 4.21 - Ahlgrim et Al. : projection de Zero coupon réel

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

4.4 Réalisation d'un cas pratique pour une compagnie d'assurance

4.4.1 Cas pratique en assurance non-vie

L'objectif de cette section est de construire un modèle ALM simplifié pour une compagnie d'assurance non-vie offrant des produits d'assurances automobiles et des produits d'assurances santé. La projection des variables macro-économiques du modèle d'Ahlgrim et Al. du bilan, du compte de résultats et de l'état de flux de trésorerie sera alimentée par les résultats issus des projections.

1. Contruction du Bilan comptable

Le tableau ci-dessous représente les hypothèses retenues pour le portefeuille étudié :

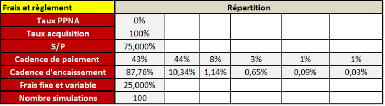
FIGURE 4.22 - Hypothéses de construction du bilan en assurance non-vie

Dans le cadre de ce mémoire et pour simplifier nous supposons que le passif est constitué seulement des capitaux propres et provisions pour sinistre à Payer (PSAP).

Pour le calcul de la psap¹ nous réalisons un triangle en fonction de la cadence de paiement on multiplie la prime acquise par le ratio s/p pour obtenir la charge sinistre qui sera répartie sur 6 ans.

A ce stade nous pouvons projeter le triangle de développement.

FIGURE 4.23 - Triangle PSAP

La variation PSAP est donnée par :

1. Provision pour sinistre à payé

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

VAR PSAP = PSAP(t) - PSAP(t - 1) Pour valider le résultat nous adaptons un back-testing:

Reglement - VAR PSAP = charge de sinistre

FIGURE 4.24 - Règlements et charges des sinistres

L'actif est constitué des placements, créance et l'avoir en banque.

Pour les créances nous réalisons un triangle d'encaissement dont la somme de chaque colonne du triangle donne le montant du règlement et la somme restante de la ligne en dehors de cette colonne donne le montant de la créance restante.

Les avoirs en banque représentent la différence entre la clôture de l'exercice présenté au niveau l'état de flux de trésorerie et l'investissement en action, obligation, monétaire et immobilier à l'année n.

Pour que le bilan soit cohérent nous vérifions que :

Total actif (t) - total passif (t) = 0

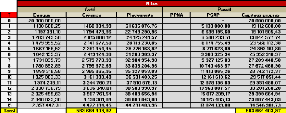
FIGURE 4.25 - Bilan économique

2. Construction du compte de résultat technique

Le compte du résultat technique nommé aussi état des résultats ou compte du résultat est un état financier synthétisant l'ensemble des charges et des produits d'une entreprise ayant une activité marchande.

Le compte de résultat technique étudié est constitué de .

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· Primes acquises

Prime acquise(t) = prime émise(t) * taux d^'acquisition avec:

(a) Prime émise(t) = prime émise (t - 1) * (1 + taux d^'inflation(t) + 2%)

(b) Taux d'acquisiton = 100% défini en hypothèse.

· Charge de sinistre

La charge de sinistre est constitué de la varisation PSAP et des sinistres réglés obtenus du triangle de développement élaboré précédemment.

· Frais d'exploitation

Frais d^'acquisiton(t) = prime émise(t) * taux de frais

· Produit financier

Ainsi le résultat tehnique est obtenu comme :

Résultat technique (t) = prime acquise (t) + sinistre réglé (t) + variation PSAP (t) + frais(t) + produit financier (t)

FIGURE 4.26 - Compte de résultat technique

3. Construction d'un état de flux de trésorerie

L'état de flux de trésorerie appelé aussi l'évolution de la situation financière indique comment l'encaisse a évolué au cours de l'exercice.

L'état des flux de trésorerie est subdivisé en trois types d'activité : l'activités d'exploitation, l'activité d'investissement et l'activité de financement.

· Activité d'exploitation elle est définie par deux éléments : l'ouverture et la clôture.

(a) L'ouverture est définie comme suit

Ouverture (0) = capitaux propres (0) pour t = 0 Ouverture (t) = clôture (t - 1) pour t > 0

(b) La clôture est définie comme la somme du solde avant placement et le produit financier de la même année.

· L'activité de financement est constituée de :

(a) Primes encaissées résultantes du triangle réalisé par la cadence d'encaissement.

(b) Sinistre (t) = sinistre réglé (t) provenant du compte de résultat technique.

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

(c) Frais (t) provenant du compte de résultat technique.

· L'activité d'investissement

Le montant à placer est défini comme suit :

(a) Montant à placer (0) = 0.

(b) Montant à placer (t) = Clôture (t-1).

(c) Excédent (t) = Prime encaissés (t) + sinistre (t) + frais (t)

(d) Solde avant placement (t) = excédent (t) + ouverture (t)

Le produit financier à l'année t est défini comme étant le total des rendements nets obtenus suite aux investissements.

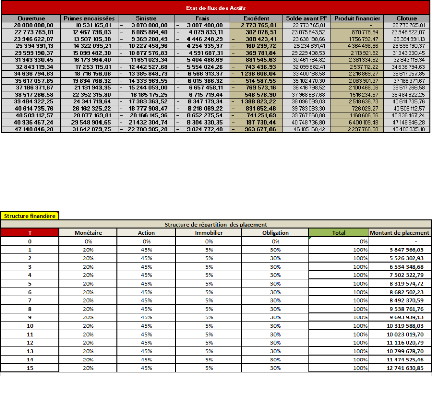
FIGURE 4.27 - Etat de flux de trésorerie

FIGURE 4.28 - Allocation stratégique des actifs

Dans ce paragraphe, nous proposons différentes allocations d'actifs afin d'étudier leur impact sur la variation du passif:

· Scénario 1 : 5 % en monétaire, 10 % en action, 10 % en immobilier et 65 % en obligation.

· Scénario 2 : 5 % en monétaire, 25 % en action, 50 % en immobilier et 10 % en obligation.

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· Scénario 3 : 5 % en monétaire, 45 % en action, 10 % en immobilier et 40 % en obligation.

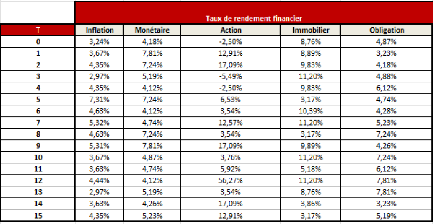
FIGURE 4.29 - Rendements macro-économiques prospective issus des GSE

4.4.2 Résultats en assurance non-vie

Nous avons développé un outil sur VBA-Excel pour projeter le bilan économique, le compte de résultat technique et l'état de flux de trésorerie au sein d'une entreprise d'assurance à l'aide des résultats issus des techniques de boostrapping sous l'allocation d'actif proposée. Les différents résultats statistiques s'affichent lors de l'exécution du code par le bouton "simuler".

Les statistiques relatives aux capitaux propres obtenus suite à l'exécution de ce scénario à l'aide de la commande VBA "Simuler" sont :

· Une moyenne de 47100.

· Un écart-type de 6465.

· Un Coefficient de variation de 14%.

Pour le deuxième scénario nous proposons l'allocation suivante: 10 % en monétaire, 10%

en action, 50 % en immobilière et 20% en obligataire, les statistiques relatives aux capitaux propres issus de ce scénario :

· Une moyenne de 55433.

· Un écart-type de 4844.

· Un Coefficient de variation de 9%.

Pour le dernier scénario proposé, l'allocation prise en compte est la suivante : 20 % en

monétaire, 30% en action, 20 % en immobilière et 20% en obligataire, les statistiques relatives à ce scénario donnée sont :

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· Moyenne: 58833.

· Ecart-type : 17900.

· Coefficient de variation: 30%.

Conclusion :

Pour le premier scénario, nous optons d'investir plus en obligataire qu'en action et immobilier nous trouvons une moyenne assez réduite par rapport aux autres scénarios, une volatilité plus élevée ainsi un coefficient de variation élevé en moyenne de 14%.

Pour le deuxième scénario, nous choisissons d'investir la moitié du montant dédié en immobilier, nous arrivons à avoir un coefficient de variation la plus réduite, une moyenne de 55433 acceptable par rapport aux autres scénarios, et un écart-type légèrement élevé en comparant les valeurs d'écart-type réalisé.

Le dernier scénario possède le coefficient de variation le plus élevé soit de 30% néanmoins on remarque qu'il possède la moyenne la plus élevée.

En effet plus que la moyenne est élevée plus que l'investissement est rentable et plus que l'écart-type est élevé plus que l'investissement est risqué, autrement dit l'investissement le plus rentable est celui qui possède le coefficient de variation le plus réduit, nous choisissons pour ce fait le deuxième scénario.

4.4.3 Cas pratique en assurance vie

Dans cette partie nous étudions le cas d'un contrat d'épargne en assurance vie afin de calculer la « Valeur Actuelle Net » et le « Best Estimate ».

Nous rappelons ces notions :

· Le VAN ¹ est défini comme étant la marge de l'assureur attendue lors d'un investissement proposé : c'est la somme actualisée de la marge de l'assureur sur les investissements.

· Pour le best estimate correspond à la moyenne pondérée par leur probabilité des flux de trésorerie futurs compte tenu de la valeur temporelle de l'argent (valeur actuelle attendue des flux de trésorerie futurs) estimée sur la base de la courbe des taux sans risque pertinent.

· Hypothèses Les hypothéses qu'ona retenus sont : - Hypothèses relatives à l'actif

Pour simplifier l'étude nous nous restreindrons à un actif constitué des actions et des obligations.

On suppose que les produits financiers à chaque période correspondent à 1 - á du rendement zéro-coupon 10 ans et á du rendement action, on note TPF (t) le taux de produits financiers et on le définit par :

T P Ft = á( P (t, M) (4.4.1)

P (t - 1, M + 1) - 1) + (1 - á)( 8(t)

8(t - 1) - 1)

Avec :

1. Valeur Actuelle Net

1. Cox-Ingersoll-Ross

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

* á : Part de l'investissment à partir du montant dédié.

* P(t,M) : Prix du zéro-coupon à un instant t de maturité M. * S(t) : Prix de l'action.

- Hypothèses relatives au passif

A noter que ce contrat est soumis au risque de mortalité et pouvant être racheté a tous moment.

L'assuré de ça part, avec un PM initial égal à 100 bénéficie d'une revalorisation annuelle correspondant au maximum entre un TMG fixé à 2% et une quote-part (fixée à 90%) des produits financiers générés par les actifs en représentation des PM.

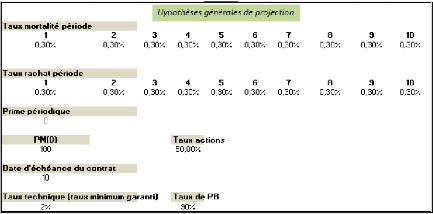
FIGURE 4.30 - Hypothéses de projection en assurance-vie

Pour la projection des facteurs financiers :

· Projections des actions

Les actions retenus pour la projection du portefeuille sont issues du GSE construit dans la premiére section de ce chapitre.

· Projection des prix zéro-coupon

Les prix zéro-coupon sont calculés à partir des taux zéro-coupon issus du GSE modèlisé. Pour passer au monde risque-neutre, nous avons utilisé le modèle CIR¹ (nous n'avons pas utilisé la méthode de risque neutralisation habituelle car nous ne disposons pas d'une courbe de taux sans risque).

Pour la projection des cash-flows:

· L'évolution du nombre de contrat (N(t)) est proportionnelle au taux de survie (S(t) = 1-q(t)) et le taux de non-rachat (r(t)).

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

FIGURE 4.31 - Résultat de projection des facteurs financiers

· L'évolution du nombre de décès (q(t)) est le produit du nombre de contrat pour l'année précédente (N(t-1)) et le taux de mortalité (q(t)).

· Le nombre de rachat (r(t)) est le produit du nombre de contrat pour l'année précédent et le taux de survie (1-q(t)) avec le taux de rachat.

· Sous l'hypothèse de l'absence des primes périodique la prime ici est nulle (nombre de contrats * prime).

· La prestation au décès est égale à la provision mathématique dédiée à l'année précédente (PM (t-1)) multiplié par le taux de mortalité (q (t)).

· La prestation au rachat est égale à la PM de l'année précédente (PM(t-1)) multiplié par le taux de rachat (r(t)) tant que l'assureur en vie (1-q(t)).

· Le montant total de bénéfice (IC Stock) dédié à être servie aux assurés est égal au montant des provisions mathématiques PM(t-1) tant que les assurés sont en vie (1-q(t)) et n'ont pas racheté leur contrat (1-r(t)) : c'est ce que la compagnie doit fournir comme stock pour faire face à ses engagements de revalorisation envers ses assurés.

· Ce que doit l'assureur avoir en stock pour servir les prestations en cas de rachat ou de mortalité (PB stock) est le maximum entre TMG et le taux de participation au bénéfice projeté pour l'année précédente (PB(t-1) projeté) pour les assurés en vie (1-q(t)) et non-racheté (1-r(t)).

· L'IC (ce que l'assureur doit l'avoir) pour les prestations est la multiplication de la PM(t) et le TMG pour les rachetés et non décès (r(t) (1-q(t)) où pour les décès (q(t)).

· La provision (PB Prest) est donné donc par le maximum entre la différence Tx PB projetée, TMG multiplié par PM(t-1) pour les rachetés et non décès ou bien décès.

· A un instant t, la PM est la somme de la PM(t-1) pour les non-décès et non rachetés, le montant de PB que doit l'assureur fournir (IC stock) et la provision dédiée pour les prestations (PB stock).

· La marge de l'assureur est PM(t-1) multiplié par la différence entre le taux du produit financier et le max (tx pb projeté; TMG) (qui sera servie à l'assuré)

· Le cash-flow du passif de l'assureur est la somme des engagements de l'assureur en éliminant la prime (elle est nulle dans notre cas).

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

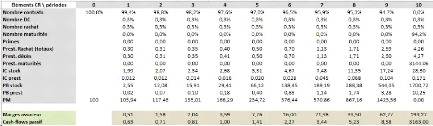
FIGURE 4.32 - Projection des cash-flows passif en assurance-vie

Pour le calcul du BE(0) et NAV(0) on recoure aux techniques des simulations à l'aide du logiciel VBA-Excel.

Une fois qu'on a déterminé la marge assureur et le cash-flow passif on s'arrange au calcul du VAN grâce au déflateur.

On effectue 1000 simulations pour la VAN marges-assureur et pour la VAN cash-flows passi et on aura:

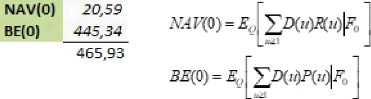
FIGURE 4.33 - Résultats BE(0) et NAV(0)

4.4.4 Résultats en assurance vie

On refait le même travail élaboré en assurance non-vie, nous utilisons VBA-Excel pour développer un bouton "Simulation VAN" afin de simuler la VAN marge assureur et la VAN cash-flow passif pour plusieurs scénarios selon le choix de á nous disposons pour ce fait deux scénarios possibles.

Le premier scénario prend une valeur de á = 20% soit une allocation de : 20% en actions et 80% en obligataires. Les valeurs issues de ce scénario sont :

· NAV(0) = -12,08.

· BE(0) = 161,95.

Pour le deuxième scénario nous changeons la valeur de á afin d'interpréter l'investissement le plus rentable, nous prenons á = 80% et nous obtenons :

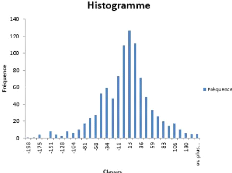
FIGURE 4.35 - Evolution du NAV selon le deuxième scénario

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

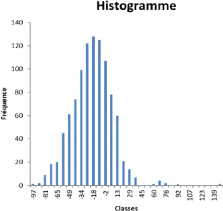
FIGURE 4.34 - Evolution du NAV selon le premier scénario

CHAPITRE 4. APPLICATION PRATIQUE DE LA MISE EN PLACE D'UN GSE ET PROJECTION AU SEIN DU MODÈLE ALM

· NAV(0) = 93,01.

· BE(0) = 1187,81. Conclusion

Pour le premier scénario nous proposons d'investir majoritairement en action soit de 80% et le reste en obligations, nous trouvons un NAV négatif et un BE trés réduit en le comparant par rapport au deuxiéme scénario.

En revanche pour le deuxiéme scénario nous prennons le cas contraire; investir à 80% en obligations et le reste en actions, nous arrivons à trouver un NAV positif et un BE beaucoup plus élevé que celle du premier scénario.

Comme indiqué dans la partie théorique le NAV constitue un outil d'aide à la décision du coup plus que ma valeur NAV est élevée plus que mon investissement est rentable de ce fait nous s'arrangeons pour le deuxième scénario et on recommande d'investir majoritairement en obligataire.

Ce choix peut être renforcé par une interprétation graphique, en effet on remarque que notre premier histogramme la distribution est plus aplati par rapport à celle du deuxième scénario, elle donne l'intuition que notre investissement est plus risqué et plus étalé.

Critiques des modèles proposés

Les résultats réalisés en amont n'impliquent pas de se limiter aux décisions fournies par le code, en effet :

· Un modèle est outil d'aide à la décision, certes son utile mais certes limitée.

· Un assureur est exposé aux différents risques, il n'est pas certain de corréler entre eux.

· Une personne averse au risque et cherche à se couvrir n'est pas capable de générer un plus de rendement.