2.3 Estimation des paramètres du modèle
ACP
L'estimation des paramétres du modèle ACP se
résume en une estimation des valeurs et vecteurs propres de la matrice
de corrélation Ó . Une décomposition spectrale de cette
dernière nous donne :
Estimation des paramètres du modèle ACP Analyse
en composantes principales
|
> >m
= P ? PT =
i=1
|
ëipipTi
|
Où: pi est le ieme vecteur propre de Ó
et ëi est la valeur propre correspondante.
S'il existe q relations linéaires entre les colonnes de
X, on aura q valeurs propres nulles. La matrice X peut être
représentée par les première (m-q) = l composantes
principales.
l correspond au nombre de valeurs propres non nulles.
Toutefois les valeurs propres égales à zéro sont rarement
rencontrées en pratique (relation quasi-linéaire, bruits, ...
etc). Donc, il est nécessaire de déterminer le nombre l
représentant le nombre de vecteurs propres correspondant aux valeurs
propres dominantes.
Pour illustrer ce qui a étédit jusqu'a
présent sur l'ACP linéaire, on va présentéun
exemple de simulation, qui sera ensuite utilisépour illustrer les
différentes méthodes
présentéprécédemment, et qui va nous suivre tout au
long de ce chapitre.
Nous disposons de 7 variables qui représentent notre
système et qui sont décrites par les équations suivantes
:
x1 = u1 + î1
x2 = u2 + î2
x3 = x1 + î3
x4 = x1 + î4
x5 = x2 + î5
x6 = x2 + î6
x7 = x2 + î7
Où: les bruits de mesureîi,j sont des
bruits aléatoires qui prennent des valeurs réparties entre -0.05
et + 0.05, u1 et u2 sont des signaux en forme créneaux dont les
amplitudes sont comme suite :
1
u1 = sin t - 3 sin 3t +
1
5 sin 5t
11
1 1
u2 = cos t- 3 cos 3t + 5 cos 5t
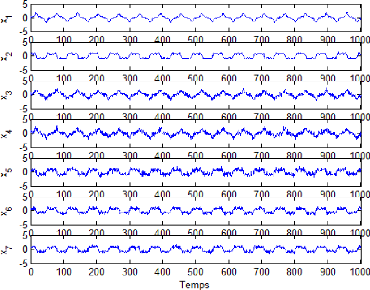
Les mesures simulées des variables sont
représentéci-dessous :
Estimation des paramètres du modèle ACP Analyse
en composantes principales
Figure 2.2 - Mesures simulées de x1...x7 du premier
exemple d'illustration
La matrice de corrélation des variables est
donnée par :
|
1.0000
|
0.0056
|
0.9269
|
0.8714
|
-0.0013
|
0.0170
|
-0.0070
|
?
|
|
0.0056
|
1.0000
|
-0.0043
|
0.0131
|
0.8807
|
0.9509
|
0.9488
|
?
|
|
0.9269
|
-0.0043
|
1.0000
|
0.8098
|
-0.0097
|
0.0029
|
-0.0151
|
? ?
|
|
0.8714
|
0.0131
|
0.8098
|
1.0000
|
0.0016
|
0.0268
|
0.0010
|
? ?
|
|
-0.0013
0.0170
|
0.8807
0.9509
|
-0.0097
0.0029
|
0.0016
0.0268
|
1.0000
0.8431
|
0.8431
1.0000
|
0.8422
0.9013
|
? ? ?
|
|
-0.0070
|
0.9488
|
-0.0151
|
0.0010
|
0.8422
|
0.9013
|
1.0000
|
?
|
X= [
12
Les matrices des valeurs et vecteurs propres sont données
par :
ë = [
|
3.6883
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
2.7443
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0.1967
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0.1845
|
0
|
0
|
0
1
|
|
0
|
0
|
0
|
0
|
0.0913
|
0
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0.0657
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0.0291
|
Estimation des paramètres du modèle ACP Analyse
en composantes principales
|
?
p=
?????????
|
0.0061 0.5133 0.0003 0.0100 0.4831 0.5018 0.5013
|
-0.5902 0.0034 -0.5772 -0.5642 0.0083 -0.0038 0.0110
|
0.1817 -0.0490 0.5537 -0.7533 0.2658 -0.1217 -0.0716
|
-0.0534 -0.1848 -0.1744 0.2411 0.8284 -0.2938 -0.3191
|
0.0393 0.0164 -0.0113 -0.0481 -0.0074 0.7006 -0.7106
|
0.7837 -0.0129 -0.5742 -0.2315 -0.0011 -0.0292 0.0390
|
0.0089 0.8364 -0.0126 0.0027 -0.0978 -0.3942 -0.3678
|
?
? ? ? ? ? ? ? ? ?
|
t1 =
t2 =
t3 =
t4 =
t5 =
t6 =
t7 =
|
+0.0061x1
|
+ 0.5133x2
|
+ 0.0003x3
|
+ 0.0100x4
|
+ 0.4831x5
|
+ 0.5018x6
|
+ 0.5013x7
|
|
-0.5902x2
|
+ 0.0034x2
|
- 0.5772x3
|
- 0.5642x4
|
+ 0.0083x5
|
-
|
0.0038x6
|
+ 0.0110x7
|
|
+0.1817x1
|
- 0.0490x2
|
+ 0.5537x3
|
- 0.7533x4
|
+ 0.2658x5
|
-
|
0.1217x6
|
- 0.0716x7
|
|
-0.0534x1
|
- 0.1848x2
|
- 0.1744x3
|
+ 0.2411x4
|
+ 0.8284x5
|
-
|
0.2938x6
|
- 0.3191x7
|
|
+0.0393x1
|
+ 0.0164x2
|
- 0.0113x3
|
- 0.0481x4
|
- 0.0074x5
|
+ 0.7006x6
|
- 0.7106x7
|
|
+0.7837x1
|
- 0.0129x2
|
- 0.5742x3
|
- 0.2315x4
|
- 0.0011x5
|
-
|
0.0292x6
|
+ 0.0390x7
|
|
+0.0089x1
|
+ 0.8364x2
|
- 0.0126x3
|
+ 0.0027x4
|
- 0.0978x5
|
-
|
0.3942x6
|
- 0.3678x7
|
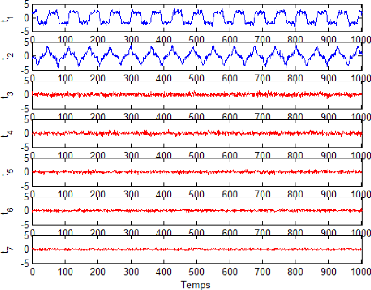
Ainsi, on peut tracer l'évolution des composantes t1, ...,
t7 de cet exemple.
13
Figure 2.3 - Evolution de toutes les composantes du premier
exemple d'illustration
Détermination de la structure du modèle Analyse
en composantes principales
14
A partir de (Fig 2.3), on remarque que les composantes t1,
..., t7 ne représentes que du bruit alors que les deux premières
composantes sont porteuse d'information et sont corrélées avec
les variables originelles (car elle sont obtenues par combinaison linaire de
ces dernires).
Cependant, pour l'estimation des variables originelles on ne
doit conserver que les composantes porteuses d'information significative
permettant d'expliquer les différentes variables. La prochaine partie de
ce chapitre sera consacréla détermination de la structure du
modèle ACP, c'est a dire la détermination du nombre de
composantes à conserver ou à retenir dans le modèle.
| 


