2.4 Détermination de la structure du
modèle
L'analyse en composantes principales a pour but
d'établir une approximation de la matrice initiale des données X,
par une matrice de rang inférieur. La question qui se pose alors et qui
a étélargement débattue dans la littérature,
concerne le choix du nombre de composantes à retenir, de nombreuses
règles sont proposées dans la littérature pour
déterminer ce nombre.
Dans le carde de l'application de l'ACP au diagnostic, le
nombre de composantes a un impact significatif sur chaque étape de la
procédure de détection et de localisation, si peu de composantes
sont utilisées, on risque de perdre des informations et voir
établir un faux diagnostic ce qui provoquera des fausses alarmes, si par
contre beaucoup de composantes sont utilisées, on risque de prendre des
composantes ayant les valeurs propres les plus faibles, qui sont porteuses de
bruit ce qui est indésirable. On peut voir ce type de composantes dans
la (Fig 2.3).
En plus il y a risque de non détection des
défauts, si certaines variables sont projetées dans le
sous-espace des composantes principale alors qu'elles doivent être
projetées dans le sous-espace résiduel.
On va citéquelques critères qui vont nous
permettre de bien choisir ce nombre.
2.4.1 Pourcentage cumuléde la variance totale
(PCV)
Il mesure le pourcentage de la variance capturée par les l
composantes retenues. Sachant que chaque composantes principale est
représentative d'une portion de la variance des mesures du processus
étudié. Les valeurs propres de la matrice de corrélation
sont les mesures de cette variance et peuvent donc être utilisées
dans la sélection du nombre de composantes principale.
Le nombre de composantes est alors le plus petit nombre pris
de telle sorte que ce pourcentage soit atteint ou dépassépar
exemple 90% ou 95% ou voir 99%.
Pl j=1 Àj
P CV (l) = 100(Im )%
j=1 Àj
Détermination de la structure du modèle Analyse
en composantes principales
15
Sa capacitéa fournir le nombre correct de composantes
principale dépend fortement du rapport signal sur bruit, car la variance
du bruit est inconnue à priori, donc ce critère reste un peut
subjectif.
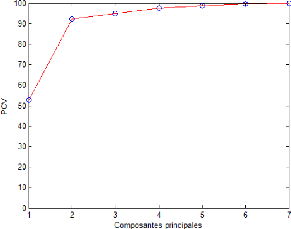
Figure 2.4 - Évolution du PCV en fonction du nombre de
composantes 2.4.2 Variance non reconstruite (VNR)
Lorsque le modèle ACP est utilisépour
reconstruire des valeurs manquantes ou des variable défectueuses,
l'erreur de reconstruction est une fonction du nombre de composantes
principale. Le minimum trouvédirectement dans le calcul du V NR
(variance non reconstruite) détermine le nombre de composantes
à retenir, le V NR de la jemme variable est
une fonction de l.
|
ój (l) = var {îT j
(x - xj)} =
|
îT P îj j
|
|
( )2
îT j îj
|
Où: îj =
Cîj et îj
correspond au jemme colonne de la matrice
identité.
Détermination de la structure du modèle Analyse
en composantes principales
Pour trouver le nombre optimal des composantes, il faut
minimiser la variance ój (l). En considérant tous les
défauts possibles, le critère VNR à minimiser est le
suivant :
|
V NR (l) =minl
|
Xm j=1
|
ój (l)
var {îT j
x}
|
=minl
|
Xm j=1
|
ój (l)
îT P îj j
|
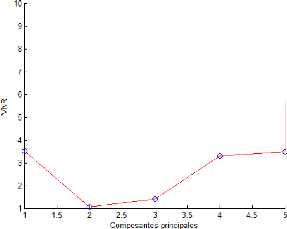
16
Figure 2.5 - Évolution du VNR en fonction du nombre de
composantes 2.4.3 Validation croisée
La validation croisée est un critère statistique
très populaire pour le choix du nombre de composantes utile pour un
modèle ACP. Cette procédure de validation croisée est
basée sur la minimisation de la somme des carrées des erreurs de
prédiction (PRESS) entre les données observées et celles
estimées par le modèle obtenu à partir d'un jeu
d'identification différent :
|
XN
1
PRESS (l) = Nm
k=1
N étant la taille du jeu de validation.
|
Xm i=1
|
( )2
àx(l)
i (k) - xi (k)
|
Détermination de la structure du modèle Analyse
en composantes principales
17
Une version simplifiée de l'algorithme permettant le
calcul du nombre de composantes principales par la validation croisée
est la suivante :
1 - Diviser les données en un jeu d'identification et un
jeu de validation.
2 - Réaliser une ACP avec l composantes (l
= 1,...., in) sur le jeu d'identification et calculer les
critère correspondant sur le jeu de validation PRESS(1), ...,
PRESS(in).
3 - La leme composante
pour laquelle le minimum de PRESS apparait sera la dernière
composante à retenir et l sera le nombre de composantes
retenu.
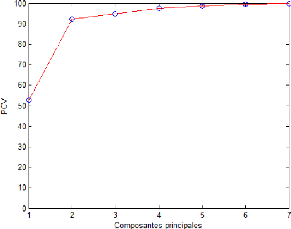
Figure 2.6 - Évolution du PRESS en fonction du nombre de
composantes 2.4.4 Moyenne des valeurs propres
Il consiste à prendre en considération que les
composantes pour lesquelles la valeur propre est supérieure à la
moyenne arithmétique de toutes les valeurs propres.
En ACP on travaille sur des données centrées
réduites, cela revient à négliger les composantes ayant
une variance inférieur a l'unité
1
in
strace( ) = 1
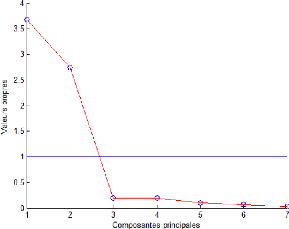
Détection de défauts Analyse en composantes
principales
18
Figure 2.7 - Évolution des Valeurs propres en fonction du
nombre de composantes 2.5 Détection de
défauts
En diagnostic à base de modèle analytique, la
phase de détection de défaut est liée à
l'étape de génération de résidus qui a pour but de
générer, à partir d'un modèle de bon fonctionnement
du processus et des mesures disponibles, des signaux révélateurs
de la présence de défauts, appelés résidus. A
partir de l'analyse de ces résidus, l'étape de prise de
décision doit alors indiquer si un défaut est présent ou
non. Il existe deux approches pour la génération des
résidus : l'approche par estimation d'état et l'approche par
estimation des paramètres. Dans ce memoire on va utiliséla
première approche.
| 


