Modélisation et diagnostic des systèmes non linéaires par acp à noyaux

2.5.1 Génération de résidus par estimation d'état

La présence d'un défaut affectant l'une des variable provoque un changement dans les corrélations entre les variables indiquant une situation inhabituelle, les relations entre les variables ne seront plus vérifiées.

La projection du vecteur de mesures dans le sous-espace des résidus va croitre par rapport à sa valeur dans les conditions normales, et le défaut nous sera alors visible, pour détecter un tel changement dans les corrélation entre les différentes variables, l'ACP utilise plusieurs indices,notamment La statistique SPE, ou T²de Hotelling.

Détection de défauts Analyse en composantes principales

19

Une fois le nombre de composantes à retenir est déterminé, la matrice X peut être approximée à partir des l premières composantes principale qui correspondent au l plus

grandes valeurs propres de la matrice :

Xà =

Xl i=1

TipT i =

Xl i=1

XpipT i

La matrice des vecteurs propres et la matrice des composantes principales peuvent

être décomposées en deux sous-matrices : P = [ P^àP] et T = [

Tà T ]

Où:
P à et

T ^àreprésentent les matrices des l premiers vecteurs propres qui correspondent aux l premières composantes principale, et l'inverse pour P et T représentent les matrices des (m - l) vecteurs propres qui correspondent aux dernières composantes principales. Sachant que _TN×m est donnée par:

T = X P = X [ Pà P]

On peut dire ainsi que:

Tà = X Pà

Et :

Xà = Tà Pà T

T ^àreprésente la projection de X sur l les premiers vecteurs propre de .

T = X P

Et :

X = T P T

Où:

T représente la projection de X sur les (m - l) derniers vecteurs propres. X représente la matrice des résidus qu'on notera E.

Détection de défauts Analyse en composantes principales

20

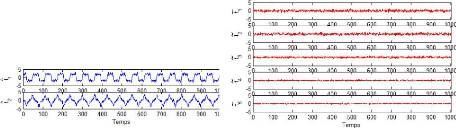
Figure 2.8 - Évolution de La projection de X sur les premiers (l) et dernièrs (m - l)
vecteurs propre de E

La décomposition de la matrice X donnera :

X = Xà + X = Xà + E

On note :

E = X C et X^à = X Cà

Oû:

C^à= P^àP^àT et C = (I - C^à)

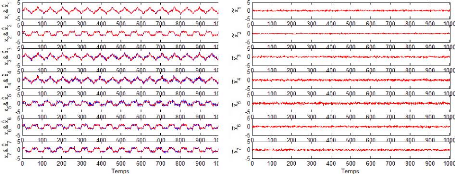
Figure 2.9 - Comparaison entre X et son estimation X^à à partir des l premières
composantes principale

Détection de défauts Analyse en composantes principales

2.5.2 Statistique SPE

L'indicateur de détection SPE (Squared Prediction Error) réalise la détection de défauts dans l'espace résiduel. A l'instant k, il est donnépar :

SPE (k) = k1 (k)k 2 = x^Tx = _Êm ~x²_j(k)

j=1

Le processus est considéréen fonctionnement anormal (présence d'un défaut) à l'instant ksi:

SPE (k) > ä²_á

Oùä² est le seuil de détection du SPE(k) qui est approximépar : :

" 2 cá V2è2h6 è2h0(h0 - 1) äá = è1 è1 + 1 + è2 1

1 h0

Soit :

èi =

m Ê j=l+1

ëi j

Pour i=1,2,3 et ëⁱ est la ^jemme valeur propre de la matrice _E .

Où: h0 = 1 - 2è1è3 3è2 2 et Cá =	[(^11e112)^h0-1-^è2h0(hè2^0-1 1
	v2è2h^2 0

C_á est la limite au seuil de confiance (1 - á).

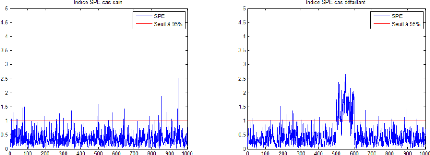
21

Figure 2.10 - Indice SPE dans le cas sain et le cas défaillant avec un seuil de 95%

Détection de défauts Analyse en composantes principales