Modélisation et diagnostic des systèmes non linéaires par acp à noyaux

2.5.3 Statistique T2 de Hotelling

L'indice T² de Hotelling mesure les variations des projections des observations dans l'espace principal. Il est calculéà partir des l premières composantes principales :

T^2(k) =

Xl i=1

àt2 i (k) Ài

Le seuil de détection peut être approximé, pour un seuil de confiance á donné, par une distribution du x².

Le processus est considéréen fonctionnement anormal (présence d'un défaut) à l'instant k si :

T2 (k) > x2 _l,á

Où:

x2 l,á = l(N - 1)(N + 1)

N(N - l) Fl,(N-l),á

Fl,(N-l),á est la distribution de Fisher avec : l, N - l degrés de liberté, et N nombre d'observations.

22

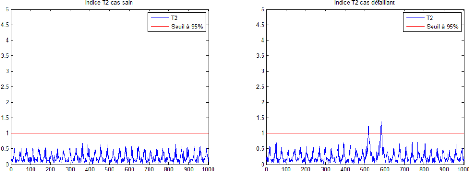
Figure 2.11 - Indice T² dans le cas sain et le cas défaillant avec un seuil de 95% 2.5.4 Localisation de défauts par ACP partielle

L'ACP partielle consiste à utiliser des bancs de modèles avec des ensembles de variables réduits et différents d'un modèle à l'autre. L'application d'une ACP sur un vecteur de données réduit oùquelques variables sont écartées par rapport au vecteur originel. Donc les résidus deviennent sensibles uniquement aux défauts associeés aux variables qui forment le vecteur réduit, et insensibles aux défauts associés aux variables éliminées.

Détection de défauts Analyse en composantes principales

La procédures consiste à structurer les indices de détection en calculant les ACP partielles ainsi que les seuils de détection des indices correspondants (Fig 2.13).

Procédure de structuration des résidus

1. Appliquer l'ACP sur la matrice des données.

2. Construire une matrice d'incidence fortement localisable (Matrice des signatures théoriques).

3. Construire un ensemble de modèles d'ACP partielles, chacune correspondant à une ligne de matrice d'incidence (prendre les variable ayant un 1 sur cette ligne).

4. Déterminer les seuils pour la détection des défauts (seuil pour T i 2 ou SPEi).

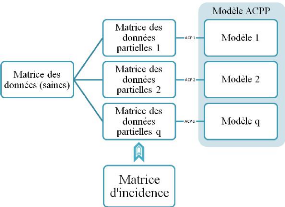
Figure 2.12 - Procèdure de structuration de résidus par ACP partielles

23

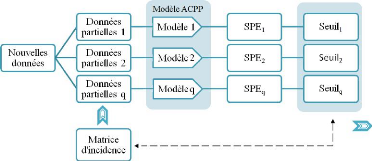
Figure 2.13 - Procèdure de localisation par ACP partielles structurée

Localisation de défauts Analyse en composantes principales

Cette approche sera utilisée pour localiser le défaut simulésur la première variable de notre exemple et qui a étédétectéprécédemment. Dans ce cas simple d'un seul défaut, on aura besoin de déterminer plusieurs modèle dont chacun est insensible à une seule variable. Par la suite, le calcul des indices de détection pour les différents modèles réduits nous permettra de localiser le défaut détecté.

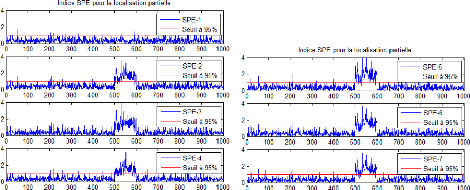
Figure 2.14 - L'évolution des SPE des modèles réduits

On remarque que le modèle ACP1 n'est pas affectépar le défaut ce qui implique que l'ACP1 est insensible à la variable en défaut X1.

24

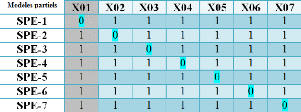
Figure 2.15 - Table des signatures théoriques