Modélisation et diagnostic des systèmes non linéaires par acp à noyaux

?'ACP à Noyau (Kernel PCA)

Sommaire

3.1 Introduction 25

3.2 Méthodes à noyaux et Kernel PCA 26

3.3 Détection et localisation en Kernel PCA 30

3.4 Algorithme de base du Kernel PCA 33

3.1 Introduction

L'Analyse en composantes principale à montréson efficacitédans le traitement des données linéaire comme on la vu dans le chapitre précédent, par contre quand il s'agit de données non linéaires on aura des difficultés à exploiter la corrélation potentielle entre les variables pour réduire la dimension. Car l'ACP consiste à trouver des relations linéaires entre les variables, or dans la projection de données non linéaires il nous est impossible de faire une séparation linéaire. Celle-ci sera erronée et pas représentative de nos variables et données. Comme le montre la figure ci-dessous :

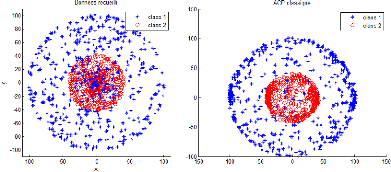
Figure 3.1 - Représentation des données non linéaire par ACP classique

25

Méthodes à noyaux et Kernel PCA L'ACP à Noyau (Kernel PCA)

26

Afin de corriger ce problème, la Kernel PCA entre en jeu, en exploitant des relations potentiellement non linéaires entre les variables. Qui aboutira par une représentation plus correct de nos données, comme le montre la figure ci-dessous :

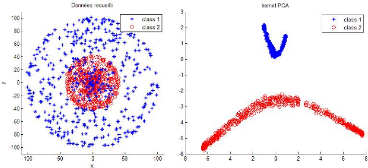
Figure 3.2 - Représentation des données non linéaires par KPCA 3.2 Méthodes à noyaux et Kernel PCA

L'ACP à noyau est une extension de l'ACP classique, qui permet d'exploiter les relations potentielles non linéaires entre les variables. Le principe de cette extension est d'envoyer nos données par une application I : R^N -? F , X -? ?(x) appelée Feature map dans un nouvel espace de grande dimension H muni d'un produit scalaire.

La kernel PCA agit sur les ?(x) de la même façon que l'ACP agit sur les Xj. Les données dans le nouvel espace fonctionnel deviennent linéairement séparables.

3.2.1 Méthodes à noyaux

Pour se familiariser avec l'astuce de noyau on va donnéquelques notions :

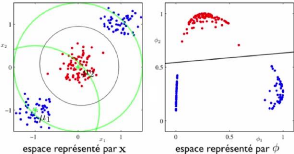
Figure 3.3 - Reprsentation en utilisant des fonctions de bases I

Méthodes à noyaux et Kernel PCA L'ACP à Noyau (Kernel PCA)

Dans la Figure (3.3) : on a deux classe différentes (bleu et rouge), il nous est impossible de trouver tout d'un seul coup une séparation linéaire entre ces deux dernières. Par contre si on utilise seulement deux fonctions de bases gaussiennes à noter :

Ij = e(- kX-ujk2

2ó2 )

OùX est le vecteur de données, et uj est un vecteur de moyenne qu'on a placéjudicieuse-ment comme le montre la Figure (3.3)

On obtient un système de représentation I1 , I2. Ainsi avec des fonctions de base on a finalement pu convertir notre problème qui était pas résolvable avec une méthode ou modèle linéaire en un problème facilement résolvable avec un modèle linéaire.

Par contre lorsque X est de grande dimension, notre représentation dans le Feature space sera d'une dimension gigantesque.

Exemple d'un mapping polynômial de X E R^d, de degréK(tous les produits entre k éléments de X), on doit calculer un (x) dans un espace de dimension et d'ordre d^k . Ex: d = 100, k = 5 donne 10000000000, ou même infinie si on prends le cas de l'exemple d'illustration gaussien-(Figure 3.3) avec X de grande dimension.

Dans la kernel PCA on utilise l'astuce du noyau qui nous laisse supposer qu'on peut calculer le produit scalaire ( (xi), (xj)) directement sans jamais avoir à calculer explicitement un (x).

Notre but est de calculer la matrice K : k(Xi, Xj) = ( (xi), (xj))

Dans la kernel PCA on utilisera le noyau gaussien pour le calcul de la matrice, ce choix est fais après le test de plusieurs noyaux connus.

K(X, Y ) = e(- 'IX-Y "2

2ó2 )

On rappelle que le noyau gaussien est bien un noyau valide, et cela peut être démontréfacilement.

Règles pour construire de nouveaux noyaux valides :

k(X, Y ) = ck1(X, Y )

k(X, Y ) = f(X)k1(X, Y )f(Y ) k(X,Y ) = q(k1(X,Y )) k(X, Y ) = _e(k1(X,Y ))

k(X, Y ) = k1(X, Y )) + k2(X, Y ))

k(X,Y ) = k1(X,Y )k2(X,Y ) k(X, Y ) = k3( (X), (Y )) k(X, Y ) = X^TAY

k(X, Y ) = k_a(X_a, Y_a) + kb(Xb, Yb) k(X, Y ) = k_a(X_a, _Ya)kb(Xb, Yb)

27

Oùc > 0, f(x)est une fonction, q(a)est un polynôme avec coefficients positifs, A est une matrice définie positive et X = (X_a, Xb). Les noyaux k1, k2, k3, k_a, et kb doivent être valides.

Méthodes a` noyaux et Kernel PCA L'ACP a` Noyau (Kernel PCA)

'Ix-Y"²

K(X, Y ) = e(- PU H²₎

On a` :

11X - Y 11² = (X - Y )^T(X - Y ) = X^TX - 2X^TY + Y^TY

K(X,Y ) = e( XT X

2ó2 )e( XT2ó2Y)e( Y ^T Y

2ó2 )

Ainsi on a démontréque ce noyau est bien valide et les règles utilisées pour arriver au noyau gaussien sont les suivantes :

1 - k(X, Y ) = ck1(X, Y )

2 - k(X, Y ) = _e(k1(X,Y ))

3 - k(X,Y ) = f(X)k1(X,Y )f(Y )