3.2.2 Kernel PCA
Aprés avoir transforménos données, on doit
construire notre modèle. On suppose
ö(Xn) = 0 )
N
pour l'instant que les données (transformées) sont
centrées (
n=1
La matrice de covariance est alors :
|
1
C = N
|
XN n=1
|
ö (Xn)ö (Xn)T
|
28
Et on cherche ses vecteurs propres vi :
Cvi = ëivi
(le défi est de trouver les vi sans vraiment calculer
explicitement la matrice C) Équivaut a` ce que vi satisfasse :
1
N
XN n=1
ö (Xn){ö (Xn)T vi} =
ëivi
On divise sur ëi et on note le scalaire : ain =
ö(Xn)T vi
ëiN
On peut donc écrire vi sous la forme :
vi = XN ainö (Xn) n=1
Méthodes à noyaux et Kernel PCA L'ACP à
Noyau (Kernel PCA)
On replace vi par cette forme et on aboutit à :
|
1 N
|
XN n=1
|
ö (Xn)ö (Xn)T
|
N m=1
|
aimö (Xm) = ëi
|
XN n=1
|
ainö (Xn)
|
Le but étant d'éliminer les ö(Xn),
et de n'avoir que des évaluations de noyau. On multiplie par
ö(Xl)T les deux côtés (Xl tiréde mon
exemple d'entrainement)
|
1 N
|
XN n=1
|
k(Xl, Xn)
|
N m=1
|
aimk(Xn, Xm) = ëi
|
XN n=1
|
aink(Xl, Xn)
|
Avec : k(Xl, Xn) = ö (Xl)T ö (Xn)
Et : k(Xn, Xm) = ö (Xn)T ö
(Xm)
OùK est la matrice de Gram : Kn,m = k(Xn,
Xm)
Sachant qu'une somme de deux éléments peut
être notéde la sorte :
N
E aink(Xl, Xn) = Kl,:ai
n=1
Où: ai est le vecteur contenant toutes les valeurs
ain comme suit :
ai = [ai1 ai2 . . . ain]T Et : Kl,: est le vecteur
contenant la lemme rangée de la matrice de Gram. On
répète la même opération pour ces sommes ce qui nous
donnera :
1
N Kl,:Kai =
ëiKl,:ai
On a ainsi obtenu une équation, on doit maintenant
généraliser ca, et générer N équations en
considérant n'importe quel Xl de l'ensemble de l'entrainement :
K2ai = ëiNKai
En multipliant par K-1, on obtient :
Kai = ëiNai
Pour obtenir les ai, on trouve les M vecteurs propres (ai) de
K ayant les plus grandes valeurs propres (ëiN)
Au final, on doit s'assurer que les vi soient de norme 1 :
|
1 = vT i vi =
|
XN n=1
|
N m=1
|
ainaimö (Xn)T ö (Xn)
= aTi Kai = ëiNaTi ai
|
29
On divise les ai par la racine carrée des valeurs propres
ëiN
Méthodes à noyaux et Kernel PCA L'ACP à
Noyau (Kernel PCA)
On peut finalement calculer chaque élément
ti(X) de la projection t(X) comme suit :
ti(X) =
0(X)Tvi = XN ain0
(Xn)T 0 (Xn) =
XN aink(X, Xn)
n=1 n=1
Centrage du noyau
On a supposéque les 0(Xn)
sont centrés, mais ce n'est probablement pas le cas. Pour avoir des
données centrés, Il nous faudrait donc soustraire la moyenne,
dans l'espace des 0(Xn) tel que :
|
1 N
(Xn) = 0(Xn)
- N E
l=1
|
0(Xl)
|
Par contre, on ne peut pas travailler avec les
0(Xn) directement, puisqu'ils peuvent être
de taille infinie. On va travailler avec la matrice (K) de
Gram tel que :
Kn,m =
0(Xn)T
0(Xm)
|
N
=
0(Xn)T0(Xm)
- N E
l=1
|
0(Xn)T
0(Xl) - 1N
|
N 1 N
0(Xl)T
0(Xm) + N2 E
l=1 j=1
|
l=1
|
0(Xj)T0(Xl)
|
30
Qui va nous donner :
|
1 ~N`
Kn,m =
k(Xn,Xm)
-NL~
l=1
|
XN
1
k(Xl, Xm) - N
l=1
|
k(Xn, Xl) +
N1 2
|
H
XN
j=1 l=1
|
k(Xj, Xl)
|
D'oùl'expression finale :
K = K - 1NK - K1N +
1NK1N Avec : 1N est une matrice N x N oùtous les
éléments sont 1N
La première chose à faire donc est de calculer
notre noyau K grâce auquel on va pouvoir trouver le nouveau
noyau K, dont on va extraire les valeurs et vecteurs
propres.
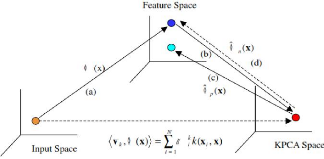
Détection et localisation en Kernel PCA L'ACP à
Noyau (Kernel PCA)
31
Figure 3.4 - Concept global du KPCA
| 


