Modélisation et diagnostic des systèmes non linéaires par acp à noyaux

?nalyse en composantes principales

Sommaire

2.1 Introduction à l'ACP 8

2.2 Identification du modèle ACP 9

2.3 Estimation des paramètres du modèle ACP 10

2.4 Détermination de la structure du modèle 14

2.5 Détection et localisation de défauts 18

2.1 Introduction à l'ACP

L'analyse en composantes principales (ACP) est une méthode mathématique d'analyse graphique de données qui consiste à rechercher et mettre en évidence les relations qui existent entre les variables, sans tenir compte, à priori d'une quelconque structure, et élabore un modèle du système à partir de données prélevées sur ce dernier L'ACP élabore un modèle du système à partir de données prélevées sur ce dernier.

L'identification du modèle repose sur deux étapes : la première consiste à estimer ses paramètres alors que la seconde consiste à déterminer sa structure.

Une fois le modèle ACP identifié, des résidus peuvent être générés en comparant le comportement observéà celui donnépar le modèle ACP de référence, Ces résidus permettent de détecter puis de localiser l'ensemble des variable en défaut.

Le but de l'ACP est donc de trouver un ensemble de facteurs (composantes) qui ait une dimension inférieure à celle de l'ensemble original de données et qui puisse décrire correctement les tendances principales.

Ce chapitre concernera la présentation et le développement des différentes procédures de diagnostics à base d'ACP en termes de traitement de données recueillies, et détection et de localisation de défauts capteurs.

Identification du modèle ACP Analyse en composantes principales

9

2.2 Identification du modèle ACP

L'identification du modèle ACP débute par la construction d'une matrice contenant l'ensemble des données disponibles sans distinction entre les entrés et les sorties du système.

Ces données sont supposées être recueillies sur un système statique en fonctionnement normal (données saines).

Au départ on aura des données recueillies sur différents capteurs x1 x_m :

Notre matrice de données X^d ? [N×m] formée par la concaténation des vecteurs xi(K) obtenus à différents instants est :

Xd (k) = [x1(K)^T x2(K)^T ... ... x_m(K)^T

Où: i [1 : m]

N étant le nombre de mesure ou itération (k) m est le nombre de capteurs ( variables ) Ce qui donnera la Matrice de données suivante :

x1 (1) ? x1 (2) Xd = ??????? . x1 (N)

x2 (1) . x2 (2) . . x2 (N) .

. . xm (1) . . xm (2) ? ??????? . . . xm (N)

Généralement les données sont exprimées par des unités et des échelles différentes. Pour cela on centre les données en premier lieu. Puis afin de rendre les résultats indépendants des unités utilisées pour les différentes variables, on réduit ces dernières par rapport a leur variance respective. Les données ainsi obtenues sont centrées et réduites, elles sont de moyenne nulle et de variance unité.

Chaque colonne Xj de la nouvelle matrice de donnée centré-réduite est donnée par :

Xj =	Xd j - Mj ój

Où: Mj = La moyenne de tout les prélèvements [1 : N] de la colonne j ój = écart type ( qui est égale à la racine carrée de la variance)

Xd j - Mj pour le centrage de nos données, qu'on divise par la suite sur ój pour la réduction.

La moyenne est donnée par :

XN 1 Mj = N k=1

xj(k)

Identification du modèle ACP Analyse en composantes principales

La variance est donnée par :

XN ó2 j = 1 N k=1

(xj (k) - Mj)^2

10

La nouvelle matrice des données normalisées est donnée par :

X = ( X1 ... X_m)

La matrice de corrélation est donnée par :

X=	1 N - 1XTX

l'effet du centrage et de réduction d'une distribution de données est illustrépar la Figure ci-dessous :

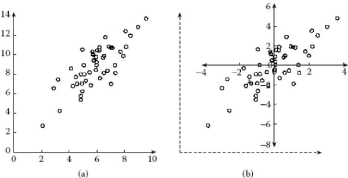
Figure 2.1 - Déroulement D'une analyse en composantes principales.(a) Distribution
d'entrée.(b) Centrage et réduction de cette distribution