Modélisation et diagnostic des systèmes non linéaires par acp à noyaux

3.3.2 Localisation de défauts par KPCA partielle

Le principe est le même que l'ACP classique, la procédures consiste à structurer les indices de détection en calculant les KPCA partielles ainsi que les seuils de détection des indices correspondants (Fig 3.6).

Procédure de structuration des résidus

1. Appliquer l'ACP à noyaux sur la matrice des données.

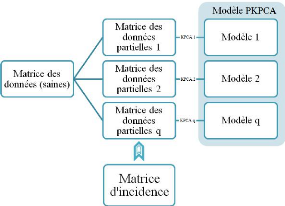
2. Construire une matrice d'incidence fortement localisable (Matrice des signatures théoriques).

3. Construire un ensemble de modèles de KCPA partielles, chacune correspondant ^àune ligne de matrice d'incidence (prendre les variable ayant un 1 sur cette ligne).

4. Déterminer les seuils pour la détection des défauts (seuil pour T i 2 ou SPEi).

Algorithme de base du Kernel PCA L'ACP à Noyau (Kernel PCA)

33

Figure 3.5 - Procèdure de structuration de résidus par KPCA partielles

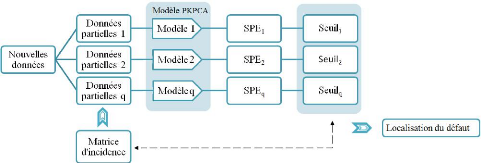
Figure 3.6 - Procèdure de localisation par KPCA partielles structurée 3.4 Algorithme de base du Kernel PCA

A la fin de ce chapitre on peut dire que l'algorithme de base de modèlisation et diagnostic à base du Kernel PCA se décompose en deux parties:

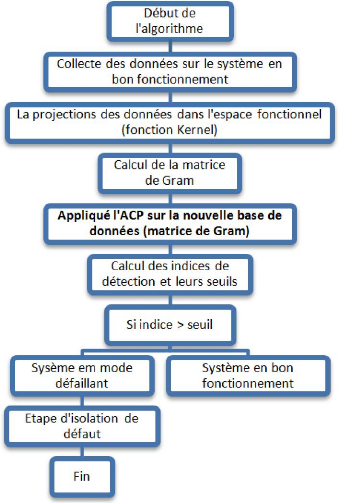
Partie 1 : Transformation de la fonction Kernel.

1. La matrice X qui contient les échantillons des différentes variables du système en bon fonctionnement.

2. Calcul de la matrice K : k(X_n, X_m) = (ö(x_n), ö(x_m)).

3. Calcul de la matrice K centrée (matrice de Gram) : G = K - 1_nK - K1_n + 1_nK1_n.

Algorithme de base du Kernel PCA L'ACP à Noyau (Kernel PCA)

Partie 2 : Application de l'ACP.

1. Diagonalisation de la matrice G (trouver les valeurs/vecteurs propres).

2. Calcul des projections sur les composantes principales.

3. Calcul des indices de détection SPE et T².

4. Développement de la procédure de localisation et isolation.

34

Figure 3.7 - Reprsentation de l'algorithme de KPCA

35