2.3. Vecteurs ou modèles
à correction d'erreur
A- Vecteur à Correction d'Erreur (VEC)
Comme souligné dans l'étude de la
cointégration, le VEC est une forme de VAR qui tient compte des
relations de cointégration. La théorie économique
n'indique pas toujours clairement comment les ajustements permettent d'arriver
à une situation d'équilibre ou à un objectif
prédéterminé. A l'aide de l'économétrie, on
arrive à combler cette lacune par des mécanismes d'ajustement
cohérents. La problématique consiste à modéliser la
variable endogène de sorte à coïncider avec une cible (la
relation de cointégration indiquant une relation d'équilibre) qui
constitue l'objectif de long terme. Le modèle à correction
d'erreur peut être construit de façon simple selon deux approches
:
- selon l'approche à deux étapes de Engel -
Granger,
- selon la méthode de Hendry en une étape
En effet, le test de cointégration permet de
déterminer . Ensuite les relations de cointégration sont utilisées
pour corriger les éventuelles erreurs qui peuvent se retrouver dans le
modèle s'il arrivait que les relations de cointégration ne soient
pas respectées à une période donnée.
La cointégration ayant été
révélée par les tests précédents, deux cas
de figure sont à envisager, il existe :
- un vecteur unique de cointégration ;
- plusieurs vecteurs de cointégration.
Si le vecteur de cointégration est unique, nous pouvons
employer les méthodes d'estimation par exemple, celle en deux
étapes de Engel et Granger.
Etape1 : estimation par les MCO de la
relation de long terme et calcul du résidu
Etape2 : estimation par les MCO de la
relation du modèle dynamique (court terme)
Cependant, le plus souvent, le vecteur de cointégration
n'est pas unique et la méthode de Engel- Granger n'est plus valide. En
effet, les estimateurs des MCO ne sont plus consistants quels que soient les
vecteurs de cointégration. Nous devons, dans ce cas, faire appel
à la représentation vectorielle à corretion d'erreur
b- Procédure d'estimation du VECM
Nous résumons ici les grandes étapes relatives
à l'estimation d'un modèle VECM.
Etape1 : Détermination du nombre
de retards p du modèle (en niveau ou en log) selon les critères
AIC ou SC.
Etape2 : Estimation de la matrice 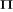 et test de Johansen permettant de connaître le nombre de
relations de cointégration (les logiciels proposent un certain nombre
de spécifications alternatives, telles que l'existence d'un terme
constant dans la relation de cointégration, l'existence d'une tendance
déterministe, etc).
Etape3: identification des relations
de cointégration, c'est-à-dire des relations de long terme entre
les variables.
Etape4: estimation par la méthode du
maximum de vraisemblance du modèle vectoriel à correction
d'erreur et validation à l'aide des tests usuels :
significativité des coefficients et vérification que les
résidus sont des bruits blancs (test de Ljung-Box).
Enfin, nous pouvons vérifier si l'estimateur par les
MCO de la relation de long terme fournit des résultats à peu
près similaires (en termes de significativité et de valeurs
estimées des coefficients) à ceux obtenus par la méthode
de vraisemblance.
La partie suivante nous donne les résultats obtenus
à partir de nos estimations.
| 
