2 .2.
Cointégration
A- Concept de cointégration
Après des tests de racines unitaires, on serait
certainement confronté au problème de l'utilisation des
séries non stationnaires dans le modèle VAR. Lorsque les
séries ne sont pas stationnaires, il existerait donc un risque de
Cointégration entre ces variables.
En effet, plusieurs propriétés statistiques ne
s'appliquent qu'à des séries stationnaires. Dès lors, il
se pose des problèmes dans la mesure où la plupart des
séries représentant des variables économiques sont
affectées par une tendance de long terme. Des simulations empiriques ont
permis à Granger et à Newbold de montrer que la distribution du t
de Student dans un modèle simple du type  en présence de racine unitaire ne peut plus être
interprété selon la loi de Student Fisher. Entre les
séries admettant des racines unitaires, il existe des
corrélations fortuites « spurious correlation » qui n'ont
aucune signification véritable et qui n'ont pas de véritables
fondements. On peut donc conclure à l'existence de relations qui, en
réalité, n'existent pas. Granger et Newbold ont montré que
ce cas est très probable si la régression a un Durbin Waston (DW)
faible et un R2 élevé. Ces résultats ont
été également confirmé de façon
mathématique par PCB Phillips qui a montré qu'en présence
de racine unitaire, le DW était aussi biaisé et tend vers la
valeur zéro. De ce fait, la question de travailler sur des séries
non stationnaires s'est trouvée poser. en présence de racine unitaire ne peut plus être
interprété selon la loi de Student Fisher. Entre les
séries admettant des racines unitaires, il existe des
corrélations fortuites « spurious correlation » qui n'ont
aucune signification véritable et qui n'ont pas de véritables
fondements. On peut donc conclure à l'existence de relations qui, en
réalité, n'existent pas. Granger et Newbold ont montré que
ce cas est très probable si la régression a un Durbin Waston (DW)
faible et un R2 élevé. Ces résultats ont
été également confirmé de façon
mathématique par PCB Phillips qui a montré qu'en présence
de racine unitaire, le DW était aussi biaisé et tend vers la
valeur zéro. De ce fait, la question de travailler sur des séries
non stationnaires s'est trouvée poser.
En claire, la cointégration se définit comme une
relation de long terme qui relie les valeurs contemporaines des variables
étudiées, bien qu'à court terme cette relation peut ne pas
être observée. Elle est, en fait, identifiée aux
combinaisons linéaires stationnaires des variables du VAR.
L'identification de cette relation lorsqu'elle existe et sa prise en compte
dans l'estimation du modèle VAR permet d'éviter de se retrouver
avec une régression fallacieuse.
B- Test de cointégration
Les tests de cointégration servent à
vérifier statistiquement l'existence des relations de
cointégration et évaluent en réalité le nombre de
relations de cointégration qui existent entre les variables. Il existe
deux méthodes :
Ø La méthode en deux étapes
de Engel et Granger
Lorsque les variables sont intégrées d'un
même ordre, cette méthode propose de faire d'abord une
régression statistique entre ces variables, récupérer les
résidus comme de nouvelles variables, puis de tester la
stationnarité des résidus à l'aide des tests de DFA. Il
faut noter que l'utilisation des tables de Dickey et Fuller n'est plus
possible. En effet, le test porte sur les résidus estimés
à partir de la relation statistique et non pas sur les
« vrais » résidus de la relation de
cointégration. MacKinnon (1991) a donc simulé des tables qui
dépendent du nombre d'observations et du nombre de variables
explicatives figurant dans la relation statistique.
Ces variables sont alors dites cointégrées,
lorsque ce test conclut en la stationnarité desdits résidus.
Ø La méthode de
Johansen
Ce test est fondé sur l'estimation du modèle
suivant :
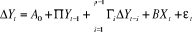 avec avec  et et 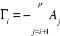
La matrice  peut s'écrire sous la forme peut s'écrire sous la forme  où le vecteur où le vecteur  est la force de rappel vers l'équilibre, est la force de rappel vers l'équilibre,  le vecteur dont les éléments sont les coefficients des
relations de long terme des variables. Chaque combinaison linéaire
représente donc une relation de cointégration et le vecteur dont les éléments sont les coefficients des
relations de long terme des variables. Chaque combinaison linéaire
représente donc une relation de cointégration et  est stationnaire. Le rang de la matrice est stationnaire. Le rang de la matrice  détermine donc le nombre de relations de cointégration.
En effet, de façon générale, dans un modèle
à une variable à expliquer et k variables explicatives (soit k+1
variables au total), il peut exister k vecteurs de cointégration
linéairement indépendante. C'est le nombre de vecteurs de
cointégrations linéairement indépendants qui est
appelé le rang de la cointégration. Johansen (1988) propose un
test fondé sur les vecteurs propres correspondant aux valeurs propres
les plus élevés de la matrice détermine donc le nombre de relations de cointégration.
En effet, de façon générale, dans un modèle
à une variable à expliquer et k variables explicatives (soit k+1
variables au total), il peut exister k vecteurs de cointégration
linéairement indépendante. C'est le nombre de vecteurs de
cointégrations linéairement indépendants qui est
appelé le rang de la cointégration. Johansen (1988) propose un
test fondé sur les vecteurs propres correspondant aux valeurs propres
les plus élevés de la matrice 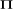 . A partir des valeurs propres de la matrice . A partir des valeurs propres de la matrice 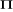 , on calcule une statistique : , on calcule une statistique :

Avec N : le nombre d'observations
k : nombre de variables.
r : 0 ;..... ; k -1, rang de la matrice 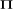
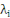 la ième plus grande valeur propre de la matrice la ième plus grande valeur propre de la matrice . .
 est appelée la " trace statstic" est appelée la " trace statstic"
Cette statistique suit une loi de probabilité
(similaire à un  ) tabulée à l'aide de simulations par Johansen et
Juselius (1990). Ce test de Johansen fonctionne par exclusion
d'hypothèses alternatives : ) tabulée à l'aide de simulations par Johansen et
Juselius (1990). Ce test de Johansen fonctionne par exclusion
d'hypothèses alternatives :
- rang de la matrice  égal 0 (r =0), soit H0 : r=0 contre
H1 : r>0 ; si H0 est égal 0 (r =0), soit H0 : r=0 contre
H1 : r>0 ; si H0 est
refusé, on passe au test suivant (si  > à la valeur critique lue dans la table, on rejette
H0) ; dans le cas contraire, la procédure est
arrêtée, et le rang de la matrice est r = 0 > à la valeur critique lue dans la table, on rejette
H0) ; dans le cas contraire, la procédure est
arrêtée, et le rang de la matrice est r = 0
- rang de la matrice 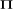 égal = 1 (r=1), soit H0 : r=1 contre
H1 : r>1 ; si H0 est refusé, on passe
au test suivant : égal = 1 (r=1), soit H0 : r=1 contre
H1 : r>1 ; si H0 est refusé, on passe
au test suivant :
- rang de la matrice 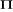 égal = 2 (r=2), soit H0 : r=2 contre
H1 : r>2 ; si H0 est refusé, on passe
au test suivant, etc. égal = 2 (r=2), soit H0 : r=2 contre
H1 : r>2 ; si H0 est refusé, on passe
au test suivant, etc.
Si après avoir refusé les différentes
hypothèses H0 à la fin de la procédure, on
teste H0 : r = k-1 contre H1 : r=k et que l'on
soit amené à refuser H0, alors le rang de la
matrice est r = k et il n'existe aucune relation de cointégration car
les variables sont toutes I(0).
En se basant sur le nombre de vecteurs propres (Eigen values)
ordonnés ou sur la valeur du rapport de vraisemblance ou le Likelihhod
Ratio (LR), fournis par les logiciels d'économétrie en fonction
du seuil choisi, on accepte ou on rejette H0. En effet, si la
statistique LR est supérieure aux valeurs critiques données au
seuil fixé on rejette H0 et on accepte H1 et on
admet qu'il y a ou non de relation de cointégration entre les
séries étudiées.
Pour mener ce test, Johansen propose cinq
spécifications concernant soit les vecteurs de cointégration soit
les séries (le VAR proprement dit)
Absence d'une tendance linéaire dans les
données
v Absence d'une tendance linéaire dans les
séries et d'une constante dans les relations de
cointégration ;
v Absence d'une tendance linéaire dans les
séries mais présence d'une constante dans les relations de
cointégration.
Présence d'une tendance linéaire
dans les données
v Présence d'une tendance linéaire dans les
séries et d'une constante dans les relations de
cointégration ;
v Présence d'une tendance linéaire dans les
séries et dans les relations de cointégration.
Présence d'une tendance quadratique dans
les données
v Présence d'une tendance quadratique dans les
séries et d'une tendance linéaire dans les relations de
cointégration.
Le choix d'une de ces spécifications s'effectue en
fonction des données et de la forme supposée de la tendance.
| 


