B- Test de Dickey Fuller Augmenté
Le test ADF est une correction paramétrique des tests
de Dickey-Fuller Simple qui supposent que les erreurs des modèles sont
des bruits blancs. Le test ADF est un cas étendu dans lequel l'erreur
suit un processus AR (p).
En effet, les distributions asymptotiques des statistiques de
test de racine unitaire ont été construites sous
l'hypothèse que  est un bruit blanc. Dès que l'on lève cette
hypothèse les statistiques des tests de Dickey Fuller ne suivent plus
les mêmes distributions asymptotiques, et donc les seuils de
significativité des tests de racine unitaire sont différents. Il
apparaît donc nécessaire de tenir compte de l'éventuelle
autocorrélation des résidus dans la construction des tests de
racine unitaire. Il existe alors deux approches différentes pour tenir
de cette éventuelle autocorrélation. La première approche,
proposée par Phillips (1987) et Phillips et Perron (1988) consiste
à proposer une correction des estimateurs des MCO et des statistiques de
Student associées à ces estimateurs prenant en compte la possible
autocorrélation des résidus. La seconde approche,
développée par Dickey et Fuller (1979), consiste à
contrôler directement l'autocorrélation dans le modèle (et
non au niveau des estimateurs) en incluant un ou plusieurs termes
autorégressifs différenciés. est un bruit blanc. Dès que l'on lève cette
hypothèse les statistiques des tests de Dickey Fuller ne suivent plus
les mêmes distributions asymptotiques, et donc les seuils de
significativité des tests de racine unitaire sont différents. Il
apparaît donc nécessaire de tenir compte de l'éventuelle
autocorrélation des résidus dans la construction des tests de
racine unitaire. Il existe alors deux approches différentes pour tenir
de cette éventuelle autocorrélation. La première approche,
proposée par Phillips (1987) et Phillips et Perron (1988) consiste
à proposer une correction des estimateurs des MCO et des statistiques de
Student associées à ces estimateurs prenant en compte la possible
autocorrélation des résidus. La seconde approche,
développée par Dickey et Fuller (1979), consiste à
contrôler directement l'autocorrélation dans le modèle (et
non au niveau des estimateurs) en incluant un ou plusieurs termes
autorégressifs différenciés.
La stratégie de test ADF consiste en une
première étape, à déterminer le nombre de retard p
nécessaire pour blanchir les résidus. Pour ce faire, plusieurs
approches peuvent être envisagées, parmi celles-ci, on peut citer
: le contrôle ex-post de l'absence d'autocorrélation des
innovations et la minimisation de critères d'information. C'est
l'approche par la minimisation des critères d'information qui sera
utilisée dans ce document.
Un critère d'information est un critère
fondé sur le pouvoir prédictif du modèle
considéré et qui tient compte du nombre de paramètres
à estimer. De façon concrète ces critères sont
construits comme des fonctions de la variance des résidus estimés
du modèle  et du nombre de paramètres à estimer. L'objectif
étant bien entendu de minimiser cette fonction par rapport à ces
deux arguments. Ces critères s'appliquent de façon
générale à tout type de modèle et pas uniquement
aux modèles des tests ADF. Nous n'en retiendrons que deux : le
critère d'Akaike et le critère de Schwarz (1978). Pour un
modèle, incluant k paramètres, estimé sur T
périodes et dont la réalisation de l'estimateur de la variance
des résidus est et du nombre de paramètres à estimer. L'objectif
étant bien entendu de minimiser cette fonction par rapport à ces
deux arguments. Ces critères s'appliquent de façon
générale à tout type de modèle et pas uniquement
aux modèles des tests ADF. Nous n'en retiendrons que deux : le
critère d'Akaike et le critère de Schwarz (1978). Pour un
modèle, incluant k paramètres, estimé sur T
périodes et dont la réalisation de l'estimateur de la variance
des résidus est  le critère d'Akaike, ou AIC, est : le critère d'Akaike, ou AIC, est :

Le critère de Schwartz (1978) est défini par :
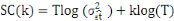 . .
Dans la seconde étape du test, il suffit d'appliquer la
stratégie séquentielle du test de Dickey Fuller Simple aux trois
modèles suivants.
Soit une série  dont on désire tester la stationnarité. Ce test s'appuie
sur les trois modèles suivants : dont on désire tester la stationnarité. Ce test s'appuie
sur les trois modèles suivants :
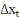 = = 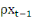 + + 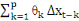 + +  (1) (1)
 = =  + +   + +  (2) (2)
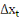 = = 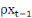 + +  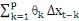 + +  (3) (3)
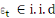 , ,
Le principe du test consiste à tester 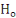 : :  (présence de racine unitaire) contre (présence de racine unitaire) contre  : : . Si l'hypothèse . Si l'hypothèse  est retenue alors le processus n'est pas stationnaire. Le test de
Dickey-Fuller augmenté consiste à estimer les trois
modèles avant de spécifier le type de processus auquel la
série est retenue alors le processus n'est pas stationnaire. Le test de
Dickey-Fuller augmenté consiste à estimer les trois
modèles avant de spécifier le type de processus auquel la
série  obéit et de procéder à sa stationnarisation. Les
étapes du test sont les suivantes : obéit et de procéder à sa stationnarisation. Les
étapes du test sont les suivantes :
1- Effectuer la régression à partir du
modèle (3)
2- Déterminer si le coefficient ( du trend est significatif du trend est significatif
3- Dans le cas contraire, reprendre la régression avec
le modèle (2) et vérifier si la constante ( est significative. est significative.
4- Si la constante n'est pas significative alors il faut
reprendre la régression avec
le modèle (1) et vérifier si  est significativement différent de 1. Si oui alors la
série est stationnaire. Si non alors elle ne l'est pas. est significativement différent de 1. Si oui alors la
série est stationnaire. Si non alors elle ne l'est pas.
| 


