6.3 Membranes presque-plates isolées.
Nous commençons en considérant des
impuretés attractives. Bien sûr, l'intégrale fonctionnelle
(5.9) ne peut être calculée
exactement. Pour faire les calculs, nous ferons usage de la méthode
variationnelle. Pour cela, nous introduisons l'action d'essai
suivante
hapitre 5 : Mécanique Statistique des
membranes confinées .. 125
[h1, ..., hn] =
f d2r
n n
Aç
[jz
E
(?há)2 + 2
E h2á ,
(5.11)
á=1 á=1
avec le nouveau paramètre de confinement
ri. Avec cette action, la fonction de partition, Zç,
est exacte, et nous avons
Zç =
(Zo)n , (5.12)
où
f { f
1~ê ]~
Z = Dhexp -
d~r 2 (?h)~ +
~ç
2h
(5.13)
est la fonction de partition habituelle d'une membrane
libre.
Introduisons alors la valeur moyenne d'une
fonctionnelle X [h1, ...,
hn], calculée avec l'action Aç
[h1, ...,
hn],
(X)0 = Zç f
Dh1...DhnX
[hl, ..., hn] exp
{-Aç [h1, ...,
hn]1 . (5.14)
En terme de cette valeur moyenne, la fonction de
partition moyenne s'écrit
Zn = Zç (exp
{- (A -
Aç)1)0 .
(5.15)
En utilisant l'inégalité
standard
(eX)0
> e<X>o ,
(5.16)
hapitre 5 : Mécanique Statistique des
membranes confinées .. 126
nous obtenons
Zn = Zç exp {- (A -
Aç~0} . (5.17)
Cela implique
|
|
|
1 - Zn
|
|
1 - Zç exp{-(A -
Aç)0}
n
|
|
|
-ln Z = lim
n?0
|
= lim
n?0
|
. (5.18)
|
|
n
|
D'autre part, nous avons
$ %
(A - A00 = f d2r u
2 E
(h2á)o
+ 8 E E
(h2áh2â)0 .
(5.19)
á=1 á=1
â=1
Il est facile de voir que
|
En á=1
|
(h2)0
= nue , á
|
En
á=1
|
En â=1
|
(h2áh2â)0
= n (n + 2)
(u2)2 , (5.19a)
|
Avec le carré de la rugosité de la
membrane
u2(ç)
=8~ ê ç . (5.20)
A l'aide de ces considérations, nous trouvons
que
-ln Z = - ln
Zo + E I u 2 u2 +
4 (u2)2] , (5.21)
avec E l'aire d'un plan de
référence. Notons le second membre de cette
inégalité
hapitre 5 : Mécanique Statistique des
membranes confinées .. 127
dépend du paramètre variationnel ri. Une
assez bonne approximation de - ln Z est
- [ln Z] CM = min r-
ln Zo + Ó (ît 2
ç~2 + 4
(ó2)2)1 (5.22)
(L'indice CM est pour thorie de champ moyen). Le
paramètre variationnel ri est tel
que
ar- ln Zo + ÓI
~u 2ç ó2 + 4
(ó2)2)1 0 .
(5.23)
La combinaison de la relation
ó2 = - 2
Ó
~ln Zo
(5.24)
En introduisant le carré de la rugosité de
la membrane habituelle (sans impuretés),
et des formules (5.19)
et (5.19a) donne la
valeur minimale de ri, qui satisfait la relation suivante
~ç =
u + . (5.25)
Le carré de la rugosité de la membrane,
ó2, est donné par les
équations paramétriques
|
{ ó2 = 1 1
8 V ç /
~ç =
~~ +
~vó2
.
|
(5.26)
|
L'élimination de ri entre ces équations
aboutit à la relation implicite
|
ó2 = 1
8
|
1
(5.27)
Vê(~u+
vó2) .
|
hapitre 5 : Mécanique Statistique des
membranes confinées .. 128
Vó~ ~ = 1/8
~ê~~, nous obtenons la
relation importante
1
ó~ =
ó~ (5.28)
V1 + vó2/~~
,
ou encore
ó2
ó2
0
1
=(impurities attractives) ,
(5.29)
V1 -
wó2/óo ,
avec la nouvelle constante de couplage sans dimensions
w = -64I
(óg)3 >
0. Notons que la constante de couplage w > 0
est directement proportionnelle à la fraction volumique des
impuretés et à l'amplitude de leur force d'interaction avec la
membrane.
Le résultat obtenu
(5.29) appelle les remarques
suivantes.
Premièrement, il n'a de sens que si
ó2/ó < 1/w. Cette
condition est remplie pour de très faibles désordres (w est assez
petite).
Deuxièmement, puisque w est défini
positive, nous avons : ó2 >
óô. Une comparaison entre cette
inégalité et celle juste évoquée au-dessus implique
que 0 < w < 1. Troisièmement, si
nous choisissons comme variable x =
ó2/óô,
nous aurons
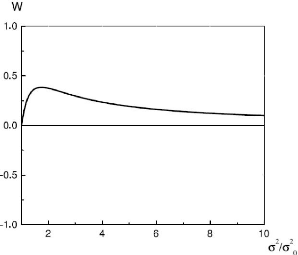
Par conséquent, w est en fonction de x
(Fig. 5.1). Cette formule peut être
expérimentalement utilisée pour estimer le couplage
d'impuretés w, à travers la mesure du rapport de rugosité
ó2/óô. Si w
est fixée à une certaine valeur, la variable x est
Chapitre 5 : Mécanique Statistique des
membranes confinées .. 129
alors solution de l'équation algébrique de
troisième degré
wx3 - x2
+ 1 = 0 . (5.31)
L'existence de ses racines dépend de la valeur
de la constante de couplage renorma-lisée w. Nous montrons qu'il existe
une valeur typique w* =
2/3V3 du couplage w séparant
différents régimes :
(i) w > w*
(désordre fort) : Dans ce régime, nous avons
une seule racine qui est négative ;
(ii) w = w*
(désordre moyen) : Dans ce cas, nous avons une
racine négative et une racine unique positive qui est x =
o2/o =
V3. Alors, la valeur maximale de la rugosité de
la membrane est o* =
31/4o0. Cette
contrainte signifie que la bicouche lipidique ne peut pas supporter les
ondulations de taille perpendiculaire supérieure à
o*. Ceci est réalisé si la fraction volumique
d'impuretés 0 est inférieure à une certaine valeur
0*, directement proportionnelle au seuil w*
;
(iii) w < w*
(désordre faible ) : Dans ce régime, nous
avons une racine négative et deux autres positives. Une seule racine
positive est acceptable (la plus petite). A cette racine particulière,
l'énergie libre -kBT [ln Z]
MF est minimale. Nous montrons que le
minimum absolu vérifie l'inégalité
Dans ce cas, le rapport
o2/o peut être obtenu en résolvant
numériquement l'équation algébrique
(5.31).
-4wx6 +
3x4 - 1 > 0
. (5.32)
hapitre 5 : Mécanique Statistique des
membranes confinées .. 130
Table 1
Certaines valeurs du couplage d'impuretés w et
les valeurs correspondantes du rapport de rugosité
u2/u2. Pour les impurities
attractives.
|
w
|
u2/uô
|
|
0.1
|
1.0575
|
|
0.15
|
1.0937
|
|
0.2
|
1.1378
|
|
0.25
|
1.1378
|
|
0.3
|
1.2715
|
|
w*
|
v3
|
Nous reportons, au Tab. I, certaines valeurs du
couplage d'impuretés w et les valeurs correspondantes du rapport de
rugosité
u2/u~~.
Il est facile de voir que ce rapport
u2/u augmente avec le couplage w, pourvu que w soit
dans l'intervalle w < w*.
Maintenant, pour des impuretés
répulsives, le rapport (5.28) doit
être remplacé
par
|
u2
u2
0
|
1
= (impuretés répulsives) ,
(5.33)
V1 +
wu2/u~o
|
ou d'une manière équivalente,
-wx3 - x2
+ 1 = 0 , (5.34)
hapitre 5 : Mécanique Statistique des
membranes confinées .. 131
Comme il devrait être, la rugosité de la
membrane est réduite par la présence
FIG. 6-1 -- Le couplage d'impuretés w en
fonction du rapport de rugosité
o2/o2 , pour les
impuretés attractives .
avec la condition de stabilité
4wx6 +
3x4 - 1 > 0
. (5.35)
L'égalité (5.34)
peut être transformée en la forme suivante (Fig.
5.2)
1 - x2
w =
s (5.36)
x
avec x < 1 et w <
0.
hapitre 5 : Mécanique Statistique des
membranes confinées .. 132

FIG. 6-2 -- Le couplage d'impuretés w
en fonction du rapport de rugosité
u2/u2
, pour le cas impuretés répulsives .
d'impuretés répulsives,
c'est-à-dire u2 <
uô. En fait, l'effet de ces particules est de
renforcer le confinement de la membrane fluide considérée. Par
conséquent, la présence d'impuretés répulsives peut
être un mécanisme de confinement d'une membrane en bicouche. Dans
ce cas, il est facile de voir que l'équation algébrique a une
seule racine positive. Au Tab. II, nous donnons quelques valeurs du
couplage w et celles du rapport
u2/uô
correspondant.
Table 2
Certaines valeurs du couplage d'impuretés w
et les valeurs correspondantes du rapport de rugosité
u2/uô.
Pour les impurities répulsives.
hapitre 5 : Mécanique Statistique des
membranes confinées .. 133
Cette définition indique que l'objet principal
à calculer est la fonctionnelle généra-
|
w
|
ó2/ó~~
|
|
-0.1
|
0.9554
|
|
-0.15
|
0.9364
|
|
-0.2
|
0.9190
|
|
-0.25
|
0.9032
|
|
-0.3
|
0.8885
|
|
-0.4
|
0.8622
|
|
~~
ä~ln Z
[J]
~
G (r -
r') = ~
äJ (r)
äJ (r')
~
|
J=0
|
.
|
(5.38)
|
Une autre quantité physique
d'intérêt est la fonction de corrélation hauteur-hauteur :
G (r - r') =
(h (r) h
(r')) - (h
(r)) (h
(r')).
Cette dernière mesure les fluctuations de la fonction hauteur h
autour d'une certaine valeur moyenne (h). Ici, (.)
désigne la moyenne thermique, qui ne doit pas être confondue
avec la moyenne sur le désordre. Pour calculer les fonctions de
corrélation, nous partons de la fonctionnelle
génératrice
Z [J] =
Dh exp -A~
[h] +
d~rJ
(r) h
(r) ,
(5.37)
avec l'action Ao
[h] = xo
[h] /kBT, où
xo [h] est le Hamiltonien
standard de Canham-Helfrich, défini par la relation
(5.1). Ici, J
(r) est une source
couplée au champ h. Les dérivées fonctionnelles
de Z [J] par rapport
à la source J définissent toutes les fonctions de
corrélation hauteur-hauteur. En particulier, le propagateur est
donné
par
hapitre 5 : Mécanique Statistique des
membranes confinées .. 134
trice connexe ln Z
[J].
Pour déterminer ln Z
[J], nous utilisons la
méthode des répliques, qui consiste à calculer la
limite
|
|
Zn
[J] - 1
n
|
|
|
|
ln Z [J] =
lim
n?0
|
,
|
(5.39)
|
avec
contribuent pas au propagateur. Après avoir
effectué la limite n = 0, nous
trouvons
" #
r
Zn [J] =
f
Dh1...Dhn
exp -A [hi,
..., hn] + J
d2rJ
(r) hi
(r) , (5.40)
i=1
où A
[h1, ...,
hn] est l'action, relation
(5.10).
Notons que l'intégrale ci-dessus ne peut
être calculée exactement. Pour avoir une valeur approximative de
cette intégrale, nous utilisons la méthode standard du cumulant
[6, 7], basée sur la
formule
(exp {X})0
= exp {(X)0 +
(1/2!)
((X2)0 -
(X) ~ + ...} .
(5.41)
~
Nous montrons que
Zn [J]
^~ Zç (exp {n
fder
fd2r'J
(r) Go
(r - r') J
(r')
/2» , (5.42)
l o
avec la fonction de corrélation
habituelle
= f
d2qGo(r
- r')
eiq.(r-r')
(5.43)
(2ð)~~êq~
+ ~ç .
Dans la relation
(5.42), nous avons
négligé les termes d'ordres supérieurs en J, qui
ne
hapitre 5 : Mécanique Statistique des
membranes confinées .. 135
que la moyenne ln Z
[J] est telle que
ln Z [J]
- ln Zo+Ó
(;ó2 +
(ó2)2)
+ 2 fd2r
f
d2r'J
(r) Go
(r - r') J
(r') .
(5.44)
Par une simple dérivation fonctionnelle, nous
obtenons l'expression du propagateur
G(r -
r') = Go
(r - r') =f
q2~ (5.45)
(2ð) rie
+~ç .
Ainsi, le propagateur attendu s'identifie avec
l'usuel. Ici, le paramètre variationnel ~ç
satisfait la relation explicite
(5.24). De cette expression, nous
déduisons la rugosité ó
(~ç)
= G (0), qui est exactement définie
par la relation (5.20).
Le but du paragraphe suivant est une extension de
l'étude à des vésicules fermées. Plus exactement,
nous chercherons à quantifier les effets de la présence
d'impuretés sur leur forme d'équilibre.
| 


