.2 Formulation théorique.
Nous considérons une membrane liquide
fluctuante, qui est confinée entre deux murs parallèles
interactifs 1 et 2. Nous
désignons par L leur distance de séparation finie.
Naturellement, la séparation L doit être comparée
à la rugosité en volume de la membrane,
eo?, quand le système est
illimité (membrane libre). La membrane est confinée
seulement lorsque la condition L <<
eo? est satisfaite.
Dans la représentation de Monge, un point de la
surface peut être décrite par un vecteur-position
tridimensionnels, r = (p, z)
E R3, où p
= (x, y) E R2
est le vecteur transverse et z = h
(x, y) E
[-L/2,
L/2]. La distance perpendiculaire est comptée du
plan localisé à z = 0. Ici, la
fonction de hauteur h (x, y)
peut prendre des valeurs positives ou
négatives.
Le Hamiltonien, 7-lo, est celui de
Canham-Helfrich [10, 30], avec une
tension de surface nulle (u =
0),
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 101
avec la constante élastique [31]
_ 9kBT
u L4 .
(4.2)
4
Ici, ê est la constante de
rigidité de courbure. Cette dernière est comparable à
l'énergie thermique kBT, où T est la
température absolue et kB est la constante de Boltzmann. En
fait, le terme
uh2/2
décrit le potentiel de confinement assurant la localisation de
la membrane autour d'un plan d'équilibre. L'intégrale ci-dessus
représente la perte d'entropie due au confinement de la membrane. La
valeur (4.2) de la constante
élastique est compatible avec la contrainte que
1 kBT L2
2? =
(h2) - (h)2 =8
vuê 12 , (4.3)
à condition qu'on soit dans le régime de
confinement où L << e1. La
quantité mesurant les fluctuations, est une fonctionnelle de la hauteur
(amplitude de fuctuations) autour d'un plan d'équilibre,
localisé à z = 0. Nous rappelons que le
résultat (4.3) a
été obtenu récemment dans la Réf. [31]
.
Maintenant, nous considérons un assemblage de
N particules colloïdales qui sont mobiles autour d'une membrane
fluide fluctuante. Pour simplifier les calculs, les particules sont
supposées ponctuelles. En fait, cette supposition a un sens, seulement
si la dimension des particules est plus petite que la rugosité de la
membrane, e? =
L/2v3. Typiquement,
les particules considérées ont un diamètre de quelques
nanomètres, en comparaison avec la rugosité qui est de l'ordre de
1 micromètre. De plus, nous supposons qu'il n'y a
aucune interaction directe colloide-colloide. Cette hypothèse reste
valable tant que la dispersion colloïdale est de faible densité.
Nous rappelons que, dans ce chapitre, nous nous intéressons à
l'influence des ondulations
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 102
de la membrane sur le mouvement des particules. Bien
sflr, les interactions mutuelles primitives entre nanoparticles devraient
être prises en considération, quand on s'intéresse à
leur transition de la phase (agrgation collodale), près d'une
interface fluide attractive [20].
Le Hamiltonien total décrivant la physique des
colloids et membrane, s'écrit [19].
H [h] =
Ho [h] + Hcm
[h] , (4.4)
avec le Hamiltonien Ho
[h], relation
(4.1). Dans la définition
précidente, Hcm représente l'interaction colloïde-interface.
Généralement, cette dernière est une fonction
compliquée des positions des particules et des configurations de la
surface. Il est alors naturel de comparer la distance caractéristique
î? (de l'ordre du micromètre) à la taille des particules
(de l'ordre de quelques nanomètres). Si nous nous intéressons au
régime où l'interface subit de fortes fluctuations, la taille des
particules est plus petite queî?. En fait, cette hypothèse permet
de négliger les effets de taille finie. Même avec cette
simplification, Hcm reste encore être compliqué. Pour simplifier,
nous supposerons que le potentiel d'interaction colloïde-surface est de
contact, c'est-à-dire
|
w
Hcm = -
2
|
N i=1
|
S [zi - h
(pi)] . (4.5)
|
Ici, S (z) est la
fonction de Dirac. Dans cette définition, la somme discrète porte
sur toutes les positions des particules, ri = (pi,
zi), avec 1 = i = N. Ici, w > 0
est la constante de couplage de surface. En fait, w joue le rôle
de la longueur d'extrapolation, rencontré habituellement dans
le contexte des Phénomènes Critiques
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 103
de Surface [32 -
34]. Dans ce modèle, l'interface est supposée
pénétrable, et les colloïdes peuvent se trouver des deux
côtés de l'interface. Comme il est montré dans Réf.
[20], les ondulations de la membrane induisent des
interactions à un et deux corps, et même plus, entre les
colloïdes. Le calcul exact de ces interactions effectives a
été accompli en utilisant la méthode du cumulant
standard, qu'on rencontre en Théorie de Champ Statistique
[35, 36].
Le système physique que nous
considérons, par la suite, est une suspension très diluée
de colloïdes identiques, qui sont au contact d'une membrane fluide
fluctuante. Donc, les interactions mutuelles entre particules peuvent
être ignorées, et la seule interaction restante est un potentiel
à un seul corps (attractif), U
(z), entre colloïdes et interface. Son
expression est [20]
~ --
2
U (z) =
Uo exp L2, (4.6)
avec l'amplitude négative
Uo = - \/3 2ð L
kBT . (4.7)
La quantité |Uo| est la
profondeur du potentiel. Notons que, dans l'expression du potentiel
d'interaction obtenue dans un travail antérieur [20],
la rugosité î? est remplacée par son expression : î?
= L/2s/3.
Faisons des commentaires à propos de
l'expression du potentiel extérieur ci-dessus, ressenti par les
nanoparticules.
Premièrement, en plus de la distance
perpendiculaire z, le potentiel d'interaction dépend naturellement de la
séparation L entre les parois réfléchissantes et de la
constante couplage de surface w.
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 104
Deuxièmement, le potentiel à un corps
passe par un seul minimum situé à z =
0. De plus, il est symétrique autour du point
minimum.
Troisièmement, la remarque est que la
profondeur de potentiel, |U0|, dépend de trois
types de paramètres, qui sont la température absolue T,
la constante de couplage de surface et l'épaisseur du film L.
Par exemple, si T et w sont fixées, la profondeur du
potentiel est inversement proportionnelle à la séparation
L. Cela signifie que le potentiel externe ressenti par les perles n'a
de valeurs appréciables, que pour des membranes se trouvant dans des
fentes très étroites. Si T et L sont maintenant
fixées à certaines valeurs, la profondeur du potentiel augmente
linéairement avec la constante de couplage surface
w.
Quatrièmement, nous soulignons que
|U0| doit être petite, en comparaison avec
l'énergie thermique kBT. Cela implique que la constante de
couplage de surface w !doit bornée supérieurement,
c'est-à_dire w < w* = L
x 2ð/3.
Enfin, comme il se doit, en l'absence d'interactions
entre colloïdes et membrane (w =
0), le potentiel à un corps disparaît. Le potentiel
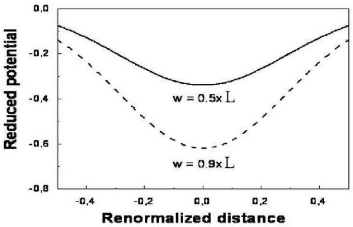
(réduit) ressentis par les nanoparticules,
U(z)/kBT, en
fonction de la distance perpendiculaire renormalisée, z/L, est
celui représenté sur la Fig.
4.1, pour deux valeurs de la constante de
couplage de surface : w1 = 0, 5
x L et w2 = 0, 9
x L. La courbe dessinée avec le paramètre
w2 est naturellement en dessous de celle avec une
constante de couplage de surface w1 <
w2.
L'expression ci-dessus du potentiel à un corps
est l'ingrédient principal pour l'étude de la dynamique Browienne
des particules de très faible densité, qui sont situées
à proximité d'une membrane souple. Mais, afin de faciliter les
calculs et obtenir des résultats exacts, l'expression ci-dessus pour le
potentiel extérieur doit
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 105
est la constante élastique. La relation
précédente montre que la constante élasique
FIG. 5-1 -- Le potentiel (réduit) ressentis par
les nanoparticules, en fonction de la distance perpendiculaire
renormalisée, z/L , pour deux valeurs de la constante de couplage de
surface : w1 = 0, 5 x L et w2 =
0, 9 x L
être simplifiée. Puisque l'essentiel du
phénomène se produit dans l'intervalle |z| < î?
= L/2V3, un tel potentiel
peut être approximé par [22]
U (z) ' Uo +
W (z) , z < î? ,
(4.8)
avec le potentiel harmonique
1
W(z) =
2kz2 , (4.9)
où
k = - U° =
121J2ð
L3kBT > 0 (4.10)
hapitre 4 : Dynamique Brownienne de colloïdes au
contact d'une biomembrane confinée. 106
k se comporte, en fonction de la
séparation L, comme k ~
L-3.
| 


