3.3.3 Spectre de fluctuations thermiques.
Sous l'effet de l'agitation thermique, les
molécules du milieu aqueux diffusent sur la membrane, et donc celle-ci
fluctue autour de sa position d'équilibre. De nombreuses études
[17] ont été consacrées à la
quantification de l'effet de ces fluctuations sur la forme des
vésicules. Nous nous limiterons ici au cas de membranes presque-planes.
Dans ces conditions, on peut décrire la forme de la surface dans la
représentation de Monge, où la position d'un point de la membrane
est repérée par sa hauteur h (r) =
h (x, y), par rapport à un
plan de référence parallèle à la position moyenne
de la membrane (Fig. 2.7).
L'énergie de la membrane peut alors être
linéarisée et s'exprime comme suit
hapitre 2 :Mécanique Statistique des
biomembranes. 57
kBT
\|uq|2%
U?+
ãq2 +
êq4 . (2.7)
FIG. 3-7 -- Représentation de Monge.
f [ê
]
H [h] =
d2~r 2
(?h)2 + ã
2 (?h)2 + U
(h) , (2.5)
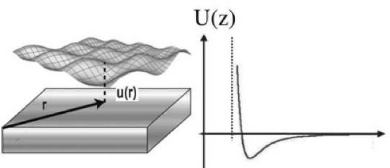
avec le potentiel extérieur U
(h), qui décrit les
interactions entre la membrane et un substrat solide ou une autre membrane.
Ici, ã est le coefficient de tension interfaciale.
Si, maintenant, on linéarise le potentiel U
autour de l'équilibre, l'énergie devient quadratique dans la
déformation h (r).
On peut donc décomposer la déformation de la membrane en mode de
Fourier d'amplitude
ti
hq = f
(27)2 h
(-r) eig.T .
(2.6)
Par ailleurs, le théorème
d'équipartition de l'énergie permet d'écrire l'amplitude
carrée moyenne de chaque mode, et l'on a
hapitre 2 :Mécanique Statistique des
biomembranes. 58
3.3.4 Interaction d'Helfrich.
Les fluctuations de forme d'une membrane lorsqu'elle
se trouve au voisinage d'un substrat solide ou d'une autre membrane, conduisent
à une interaction d'origine entropique dépendant de la
rigidité des membranes et de la température. Cette interaction a
été décrite, pour la première fois, par Helfichen
1978. Elle permet, en particulier, de comprendre la
remarquable stabilité des phases lamellaires des tensio-actifs
neutres.
Considérons une membrane de module de courbure
ê, et négligeons, dans un premier temps, la tension de surface.
Les fluctuations de cette membrane sont confinées entre deux murs
distants d'une distance finie î? (Fig.
2.9a). L'on suppose qu'il n'existe que des
interactions stériques à très courte portée entre
les murs et la membrane. L'amplitude des fluctuations de la membrane est donc
limitée par la présence des murs. On peut raisonnablement
supposer qu'un choc de la membrane sur un mur décorrélé
complètement les fluctuations. On voit alors la membrane comme une
mosaïque de patch indépendants de taille
î2II et d'amplitude de fluctuation
moyenne
î2?.
Ici, îII représente la longueur de
corrélation dans le plan. On peut maintenant relier ces deux grandeurs
en utilisant l'expression du spectre de fluctuations, définie par la
relation (2.8), avec U?=
0 et ã = 0. Alors, l'on a
kBT
0uq|2)
(2.8)
êq, ,
f d2~q
~|uq|2) ~
kBT
î2 ? ~ ê
î2 II . (2.9)

hapitre 2 :Mécanique Statistique des
biomembranes. 59
FIG. 3-8 - Une membrane liquide fluctuante , qui est
confinée entre deux plaques parallèles
.
Il reste à calculer la variation
d'énergie libre, ?FS, par unité de surface due
au confinement de la membrane. La courbure de la membrane liée à
la présence des murs est simplement donnée par
R-1 ~
îL/î2II. On en déduit la
contribution enthalpique
2
kBT
?Ec ~ ê .
(2.10)
î
2 II
Les bouts de la membrane, de taille
î2II, étant indépendants, le confinement
réduit leur entropie de kB et l'on obtient
kBT
?Sc ~ .
(2.11)
î
2 II
A l'aide de ces considérations, l'on
déduit que la variation de l'énergie libre due au confinement
est
hapitre 2 :Mécanique Statistique des
biomembranes. 60
kBT
?THelfrich ~
?Ec - T?S
~
ê
1
(2.12)
.
î~ ?
Il s'agit d'une interaction répulsive,
qui est proportionnelle à l'énergie d'agitation thermique
kBT, et inversement proportionnelle au module de courbure de la
membrane. Traditionnellement, l'on introduit une constante, cH, et
l'on écrit l'énergie de répulsion de Helfrich comme
suit
|
kBT
VHelrich `v cH
ê
|
1 .
(2.13)
î~ ?
|
Nous rappelons que de nombreuses études
théoriques et numériques ont suivis les travaux pionniers de
Helrich. Ainsi, Seifert [19] a proposé une
généralisation de l'interaction de Helfrich au cas des membranes
sous tension (ã =
0).
Dans le cas asymétrique d'une membrane neutre
qui fluctue près d'un seul substrat (ou d'une seule autre membrane),
l'interaction entropique (répulsion de Helfrich) repousse la membrane
qui peut décoller.
Noter également que les fluctuations thermiques
influent également sur les propriétés élastiques de
la membrane.
| 


