3.3 Propriétés statistiques des
biomembranes.
Dans ce paragraphe, nous rappelons l'essentiel de
l'étude des propriétés mécaniques de la bicouche
lipidique ainsi que le formalisme associé. L'outil pour cela est une
approche élaborée par Helfrich, basée sur l'énergie
de courbure.
3.3.1 Description thermodynamique.
Parmi les paramètres pertinents dans la
description d'une membrane fluide, nous pouvons citer son aire totale,AT, et
son aire projetée, AP. Ces aires sont deux variables thermodynamiques
indépendantes [6, 7]. En effet, l'aire
totale ne peut être modifiée que par échange de
molécules avec un réservoir ou par effet de dilatation (due aux
fluctuations thermiques de la membrane). Des expériences d'aspiration
par
hapitre 2 :Mécanique Statistique des
biomembranes. 53
micropipette ont montré que les
vésicules sont très résistantes aux déformations de
compression et de dilatation [9] : les membranes sont peu
extensibles et peuvent donc être considérée comme
incompressibles. La variable conjuguée à l'aire totale AT
est alors directement proportionnelle au potentiel chimique des
tensio-actifs.. En revanche, l'aire projetée AP dépend
des contraintes appliquées : cisaillement, adhésion, ..., le
paramètre conjugué étant une tension de surface. Une
propriété spéciale de ces systèmes
auto-assemblés est que, en l'absence de contraintes, l'aire
projetée d'une membrane fluctuante s'adapte, de manière à
minimiser l'énergie, et donc s'ajuste pour annuler la tension de
surface. Notons que ce point n'est pas forcément vrai pour une surface
fermée, comme par exemple une vésicule, où les
fluctuations thermiques sont responsables de la tension
[10,11].
3.3.2 Théorie de Canham-Helfrich.
La description théorique des membranes a
réellement débuté avec les travaux de Canham puis ceux de
Helfrich [12, 13]. En s'inspirant des
propriétés des films minces, les auteurs proposèrent une
approche phénoménologique basée sur l'énergie
élastique de courbure suivante
H = 2 f (C1 +
C2 - Co)2 dS
+ êG J
C1C2dS +
ã f dS , (2.1)
où C1 = R-1
1 et C2 = R-1
2 sont les deux courbures principales,
(C1 + C2) /2
la courbure moyenne (Fig.
2.6),
et C1C2 la courbure
totale (de Gauss) (Fig. 2.7).
L'énergie (2.1) peut être vue
comme un développement en puissance des invariants du tenseur de
courbure. Le der-
hapitre 2 :Mécanique Statistique des
biomembranes. 54
fCiC2dS
= 4ð (1 - g) ,
(2.2)
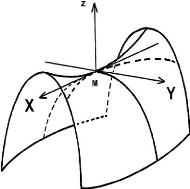
FIG. 3-5 -- Une forme de selle de cheval »dans le
cas ci=-1/ Ri<0, c2
=1/R2>0.
nier terme de cette équation est un terme de
tension de surface, et Co est la courbure spontanée
de la membrane, qui peut être associée à une
asymétrie de composition de la bicouche. Le paramètre K est la
constante de rigidité de courbure. Cette dernière a
été mesurée expérimentalement par des
méthodes d'aspiration par micropipette, ou par l'étude de
l'amplitude des fluctuations thermiques de la membrane
[14,15]. Les valeurs obtenues sont de
10 à 50kBT, pour les
membranes phospholipidiques. Quant au paramètre KG, il
représente la constante élastique de courbure
gaussienne, et est associé à la topologie de la membrane. Le
théorème de Gauss-Bonnet [16] permet
d'évaluer l'intégrale de la courbure gaussienne pour une surface
fermée sans bords. Ce théorème stipule que cette
intégrale dépend uniquement de la topologie de la surface, et
s'exprime sous la forme suivante

hapitre 2 :Mécanique Statistique des
biomembranes. 55
hapitre 2 :Mécanique Statistique des
biomembranes. 56
FIG. 3-6 -- Une forme ellipsoïydale d'une surface
dans le cas : c1 =1/R1>0 ,c2
=1/R2< 0
.
où la constante g est le genre
topologique, et correspond au nombre de poignées de la
surface (g = 0, pour la sphère, g
= 1, pour le tore). Pour un système
constitué de plusieurs surfaces fermées, on peut écrire la
contribution de la courbure gaussienne à l'énergie de courbure
comme
JêG
C1C2dS =
4ðêG (N -
Nh) . (2.3)
Ici, N est le nombre de composants
déconnectées et Nh est le nombre total de
poignées.
En fait, cette contribution à l'énergie
de courbure agit comme un potentiel chimique qui gouverne la topologie du
système. En particulier, il est important de connaître le signe de
R. C'est lui qui contrôle l'apparition de
poignées sur la surface, c'est-à-dire la formation de point
selle de courbure moyenne quasi-nulle et de
courbure gaussienne négative.
Revenons à l'énergie de courbure de
Cahnam-Helfrich et notons qu'il est possible, à partir de cette
énergie, d'étudier la stabilité d'une phase lamellaire..
Nous avons vu que le terme de courbure gaussienne est celui qui contrôle
la topologie du système, alors que les fluctuations de forme de la
surface sont gouvernées par la courbure moyenne. On peut imaginer deux
mécanismes de déstabilisation de la membrane : (i) par la
création d'un passage qui coûte une énergie
-47ri (en première approximation, le
passage est une surface minimale de courbure moyenne nulle), et l'on gagne donc
de l'énergie à créer des passages, si k
> 0, (ii) ou par formation d'une vésicule
(l'énergie de courbure d'une vésicule sphérique
étant 47r (2k + R),
et l'on gagne donc de l'énergie à créer des
vésicules, si k < -2k .
| 


