III.2. Les réseaux de neurones dans la commande
des systèmes :
Par leur capacité d'approximation universelle, les
réseaux de neurones sont bien adaptés pour la commande des
systèmes non linéaires. En effet dans ce cas la fonction commande
est une fonction non linéaire, l'objectif est alors d'approximer cette
fonction par les RNA (réseaux de neurones artificiels). Cette
approximation est réalisée par apprentissage des poids du
réseau, l'apprentissage peut se faire hors ligne ou en ligne :
ü Dans le cas de hors ligne, l'apprentissage est
basé sur un ensemble de données définissant la fonction
commande.
ü Dans le cas de en ligne, la mise à jour des
poids est essentiellement adaptative. Il existe alors plusieurs algorithmes de
commande par RNA basés sur ces deux structures, principalement on peut
distinguer :
> La commande inverse (basée sur l'erreur de
commande).
> Commande basée sur l'erreur de sortie
(d'état).
> Commande adaptative.
> Commande basée sur le critique adaptatif (Adaptif
Critique).
> Commande apprentissage d'un contrôleur
conventionnel.
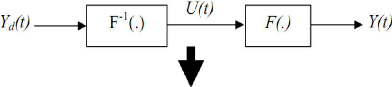
III.2 .1. La commande inverse:
Considérons un système non linéaire avec une
entrée u(t) et une sortie
y(t) peut dépendre de
u(t) seulement ou de u(t)
et les états précédents de y et/ou u
y(t)= F (u(t))
(III-1)
Ou
y(t)=F (u(t), u(t-1), u(t-2),...,
y(t-1), y(t-2),...) (III-2)
L'objectif est de faire suivre y(t) une
trajectoire de référenceyd(t). Le contrôleur idéal
réalise l'égalité : y(t)=yd (t),
mathématiquement il doit réaliser l'inverse F-1 de la
fonction F.
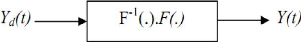
Figure III.2.principe de la commande neuronale
inverse.
Le principe de la commande inverse par réseau de
neurones consiste à construire le réseau (en
générale MLP) qui approxime la fonction F-1, cette
approximation se fait par apprentissage hors ligne. Etant donné la
fonction F, il faut construire un RNA pour réaliser l'approximation, on
génère une base de données à partir de F.
L'objectif de l'apprentissage est de déterminer la fonction inverse
à partir de ces données. A l'instant t on donne au RNA :
y(t), y(t-1), y(t-2) et on obtient à la sortie
ur(t). La mise à jour des poids du réseau est basée sur la
minimisation de l'erreur entre ur(t) et u(t)
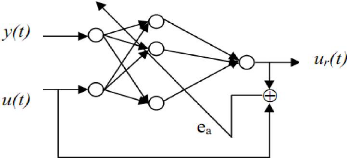
Figure III.3.Apprentissage de la commande
inverse.
/ RIAINMESSIFQtiAAMAeAMIPiAPIDLOéAeIu SIIt ~IIIIMIliAPIFRP
P 11FRQtrôleur
iQverAe. Cette
méthode peut être appliquée aux
systèmes invariants dans le temps.
III.2.2. Commande basée sur l'erreur de sortie:
DIQAADIFIA UAFeMMISSERFK, IIEA'pBfiiliéIMP 1Qe10 1FRQt>
TS 61 $ MEP IQiP iAe I
MilECTeQtrIRI ARLIHNEMPIpIeQTH IIl A'PBarlRrAuIRQaiP eQtueP
eQt dIPQ aSSIFQtiAAMITQT boucle fermée, alors faut il le réaliser
en ligne ou hors ligne. La AtIuFIMI KI111SSIeQtiAAaIe est donnée par la
Figure .III.4
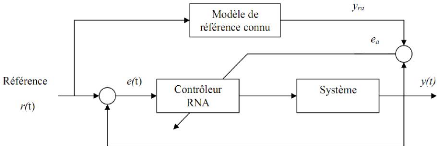
Figure .III.4.commande à modèle de
référence.
/ IRENFtiIITAt O'eQtIaîQILID14hAeIXESROUIRMllileA SRIdA
qX3P IQiP 1A1Qt
J=1/2[37ra(0 -- 37(??)]
2=1/2[ea(??)]2
(III-4)
La commande u(t) dépend des poids du réseau, la
mise à jour est alors de la forme :
???? ???? ????
??(t+1)=??(t)-?? (III-5)
???? ???? ????
Mais on ne connaît pas le Jacobien ????

????
Plusieurs propositions ont été faites pour
résoudre le problème du Jacobien, une des premières a
été de créer un émulateur qui modélise le
système.
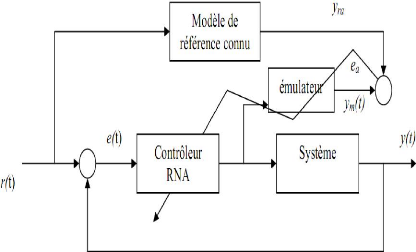
Figure III.5.structure de commande neuronale
avec émulateur Cette méthode fonctionne si ????
??) = ??(t) les étapes pour le développement de Cette approche
:
> Construire le RNA émulateur (à partir des
données).
> Initialiser hors ligne le contrôleur RNA.
| 


