III.2.3. Commande adaptative neuronale:
Dans cette stratégie de contrôle, les
réseaux de neurones sont introduits pour construire des systèmes
de commande adaptative stable basés sur la théorie de la
stabilité de Lyapunov. Deux
classes de méthodes ont été
développées: directe et indirecte.
III.2.3.1 La commande adaptative neuronale indirecte
:
Dans la première approche appelée commande
adaptative neuronale indirecte, les réseaux de neurones sont
utilisés pour approximer les non linéarités du
système non linéaire. Une des méthodes qui a connu le plus
de développement est basée sur la méthode de
linéarisation par retour (feedback linearization) avec un système
non linéaire sous forme affine :
x (t) = É (x) + 9(x)u(t)
(III-6)
Y(t) = h(x)
La loi de commande linéaire est de la forme :
U(t)=v-É(x)
(III-7)
9(x)
Lorsque les fonctions non linéaires
f(x) et g(x) sont inconnues, deux
réseaux de neurones sont utilisés pour obtenir leur
approximations É à(x) et
g(x) et construire la commande
C(t) approximée dans cette approche
se pose cependant un problème de singularité de la commande
lorsque g(x) = 0. Plusieurs
techniques ont été proposées pour éviter cette
singularité, la plus intéressante étant la commande
indirecte ci-dessous.
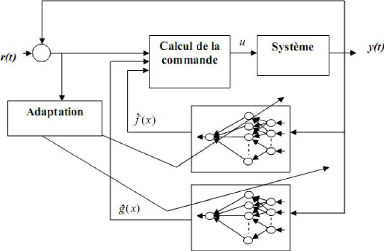
Figure III.6.schéma de commande indirecte
basée sur la linéarisation par retour. III.2.3.2. La commande
adaptative neuronale directe :
La deuxième approche appelée commande adaptative
directe le seul réseau de neurones est introduit pour approximer
directement la loi de commande idéale non constructible
u(t) cidessus. Dans ces méthodes le
signal d'adaptation est l'erreur de poursuite. Il faut noter cependant que les
développements mathématiques sont plus élaborés
pour cette méthode. Par exemple la méthode proposée dans
consiste à approximer la loi :
U (??)= ??
??(??)(É (??) +??)
+2????)2 ???? (III-8)
Où
????= ????
?? ??=?? ???? (III-9)
Avec e =[????, ????, . .
????]??=????-??????-??
i=1,...n
Et
??-??
??=-???? ??~+ ????
??=?? ???? (III-10)
???? est un signal de référence borné et
supposé n fois dérivable. Les coefficients ???? Sont choisit tel
que le polynôme ????+????-??????+...+???? a tous ses
racines strictement dans le demi plan complexe gauche et
????=1 donc
e(t)?0 tan que ???? ?0.
| 


