III.2. Ajustement du modèle
III.2.1. Ajustement graphique
Il est souvent plus facile avec les modèles IRT d'utiliser
les courbes caractéristiques pour analyser les items. CONCQOUEST offre
la possibilitéd'avoir ces courbes. Le code est donné
en annexe.
Nous avons ci-dessous deux exemples de CCI du test de langue
francophone. En trait continu, nous avons la courbe la courbe
quasi-idéal produite par le modèle et en pointillés la
courbe empirique. La CCI de l'item langj donne l'exemple d'un item qui s'ajuste
bien au modèle. L'ajustement parfait est difficile voire impossible
à obtenir.
La courbe observée, malgré l'oscillation,
épouse l'allure de la courbe théorique.
Graphique 4: courbes
caractéristiques d'un item bien ajusté au
modèle
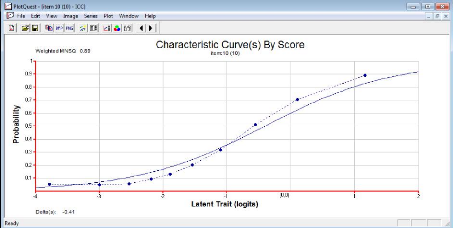
Nous avons, à l'opposé ici, un item déviant
toujours le même item lang_f (l'item 6 pour CONQUEST)
Graphique 5: exemple d'un item qui ne s'ajuste
pas bien aux données

La courbe empirique s'écarte complètement de la
courbe théorique. Pire elle décroit pour des traits latents
compris entre -1 et 1 violant l'hypothèse de monotonicité.
III.2.2. Ajustement statistique
a) Application sur R
Comme nous l'avons déjà exprimé, cette
ajustement a pour but de déterminer les items qui s'ajustent
significativement au modèle.
>item.fit(BIR)
Encadré 4: Test d'ajustement avec
R
Item-Fit Statistics and P-value Call:
ltm(formula = data ~ z1)
Alternative: Items do not fit the model Ability Categories: 10
X'2 Pr(>X'2)
FIN5F__E 24.1134 0.0022 FIN5F__A 57.8623 <0.0001 FIN5F__Q
63.7090 <0.0001 FIN5F__B 17.6695 0.0238 FIN5F__S 20.6680 0.0081
|
lang_a
|
24.6577
|
0.0018
|
|
lang_b
|
18.5878
|
0.0172
|
|
lang_c
|
36.6025
|
<0.0001
|
|
lang_d
|
33.7865
|
<0.0001
|
|
lang_e
|
30.2248
|
0.0002
|
|
lang_g
|
16.0449
|
0.0417
|
|
lang_h
|
27.9201
|
0.0005
|
|
lang_i
|
18.7033
|
0.0165
|
|
langj
|
25.2253
|
0.0014
|
|
lang_k
|
22.5732
|
0.004
|
|
lang_l
|
38.8514
|
<0.0001
|
|
lang_m 43.8923
|
<0.0001
|
|
lang_s
|
19.2971
|
0.0133
|
|
lang_t
|
20.4608
|
0.0087
|
|
lang_u
|
26.9626
|
0.0007
|
|
lang_v
|
13.5028
|
0.0957
|
|
lang_w
|
16.7123
|
0.0332
|
|
lang_x
|
26.0067
|
0.001
|
|
lang_y
|
14.7331
|
0.0645
|
|
lang_z
|
10.4916
|
0.2322
|
lang_aa 45.9957 <0.0001 lang_ab 13.2897 0.1023 lang_ac
17.0671 0.0294 lang_ad 12.5607 0.1279 lang_ae 15.4527 0.0509 lang_af 12.9743
0.1127 lang_ah 13.3439 0.1006 lang_ai 16.2935 0.0384
On conclue que 7 items seulement ne s'ajustent pas
significativement au modèle.
Notons aussi que pour évaluer la robustesse de nos
estimations nous avons testé le modèle sur un cinq sous
échantillon de l'échantillon principal (50%) tirés
aléatoirement. Les moyennes des estimations des paramètres du
modèle convergent vers le même résultat trouvé
précédemment. Nous avons développé cette
procédure sur R (voir code en annexe III).
Tableau 4 : Les moyennes et variances des
paramètres de difficulté et de discrimination des cinq
sous-échantillons sont affichées comme suit :
|
Moy. Dif
|
Var. Dif.
|
Moy. Dis.
|
Var. Dis.
|
|
FIN5F__E
|
0,9617
|
0,0013
|
1,3706
|
0,0031
|
|
FIN5F__A
|
0,4208
|
0,0009
|
1,2625
|
0,0070
|
|
FIN5F__Q
|
0,5753
|
0,0011
|
1,1143
|
0,0032
|
|
FIN5F__B
|
1,5011
|
0,0130
|
0,8576
|
0,0055
|
|
FIN5F__S
|
1,2687
|
0,0043
|
1,2627
|
0,0079
|
|
lang_a
|
0,6680
|
0,0013
|
1,3304
|
0,0098
|
|
lang_b
|
-0,0800
|
0,0023
|
0,9513
|
0,0005
|
|
lang_c
|
-0,1608
|
0,0007
|
1,9604
|
0,0029
|
|
lang_d
|
-0,1980
|
0,0011
|
1,5349
|
0,0079
|
|
lang_e
|
1,2020
|
0,0078
|
0,6503
|
0,0020
|
|
lang_g
|
0,5125
|
0,0009
|
1,9389
|
0,0017
|
|
lang_h
|
1,1426
|
0,0017
|
1,8865
|
0,0037
|
|
lang_i
|
0,8068
|
0,0016
|
2,3657
|
0,0119
|
|
lang_j
|
0,7892
|
0,0013
|
2,0160
|
0,0134
|
|
lang_k
|
0,8024
|
0,0015
|
2,2156
|
0,0240
|
|
lang_l
|
0,7655
|
0,0106
|
1,3366
|
0,0069
|
|
lang_m
|
1,2267
|
0,0023
|
1,1381
|
0,0015
|
|
lang_s
|
0,7895
|
0,0018
|
2,8302
|
0,0397
|
|
lang_t
|
0,9907
|
0,0013
|
2,8860
|
0,0210
|
|
lang_u
|
1,1847
|
0,0011
|
2,8698
|
0,0231
|
|
lang_v
|
0,9243
|
0,0004
|
2,8993
|
0,0186
|
|
lang_w
|
1,0338
|
0,0008
|
3,0018
|
0,0211
|
|
lang_x
|
0,7468
|
0,0019
|
1,6812
|
0,0061
|
|
lang_y
|
1,6409
|
0,0021
|
1,9735
|
0,0144
|
|
lang_z
|
1,9007
|
0,0078
|
1,8264
|
0,0106
|
|
lang_aa
|
1,8879
|
0,0673
|
0,5489
|
0,0075
|
|
lang_ab
|
1,1594
|
0,0010
|
2,0034
|
0,0047
|
|
lang_ac
|
1,2356
|
0,0020
|
2,2813
|
0,0081
|
|
lang_ad
|
1,5244
|
0,0035
|
2,5665
|
0,0116
|
|
lang_ae
|
1,1327
|
0,0016
|
3,0144
|
0,0105
|
|
lang_af
|
1,1924
|
0,0019
|
2,9807
|
0,0194
|
|
lang_ah
|
1,5701
|
0,0012
|
2,8218
|
0,0152
|
|
lang_ai
|
1,5667
|
0,0041
|
2,8253
|
0,0517
|
Ces résultats témoignent de la robustesse de nos
estimations. b) IIs F'a's dP'JIP
Une des contraintes majeures du cahier de charge des tests
était de s'assurer de l'équivalence des versions francophones et
anglophones des items. Le contenu des tests a été
réalisé de manière à établir un
dénominateur commun entre les programmes et méthodes
d'enseignement des deux sous-systèmes francophone et anglophone du
Cameroun. Les traductions des tests ont été
vérifiées par un cabinet spécialisé et les items
ayant des comportements similaires dans les deux versions ont été
sélectionnés après la mise à l'essai.
Les tests finaux devraient donc être équivalents
dans leur fonctionnement entre élèves francophones et
anglophones.
En première instance, une analyse comparée des
taux de réussite, indices de difficulté et de discrimination des
versions francophones et anglophones a été réalisé
et montre une grande similarité des différents valeurs des
indices calculés sur la base de la théorie du score vrai dans les
deux sous-systèmes.
Ceci étant, la théorie du score vrai ne nous
permet pas d'affirmer que les tests sont équivalents ni de
déterminer si les élèves francophones et anglophones
performent identiquement.
Il nous faut donc mobiliser une fois de plus la théorie
de réponse aux items qui proposent plusieurs méthodes
d'étude des biais ou fonctionnement différentié des items
(diferential item functionning, DIF). Ces méthodes reposent sur
deux grands principes : soit sur une fonction de l'aire entre les deux courbes
caractéristiques des items, soit un test de signification en rapport
avec les paramètres des items.
Pour simplifier, nous avons opté pour une
méthode graphique, en visualisant l'écart entre les courbes
francophones et anglophones des items. Les courbes ont été
tracées avec le logiciel Conquest.
Nous avons ci-dessous deux exemples de CCI du test anglophone et
francophone.
Le premier exemple montre une grande similarité entre
les deux items des deux tests. Quant au deuxième graphique, on remarque,
en terme de difficulté, un écart entre les deux courbes mais le
pouvoir discriminant des deux items est pratiquement le même.
Graphique 6 : CCI d'items anglophone et francophone
ayants un même pourvoir discriminant et un même niveau de
difficulté
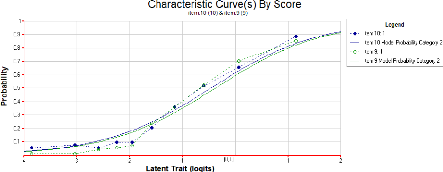

Graphique 7 : CCI d'items anglophone et francophone
ayants des niveaux de difficulté différent mais un même
pourvoir discriminant
Les graphiques n'ont pas fait ressortir d'écart
important entre courbes francophones et anglophones des items. On notera que
les items d'ancrage ont été sélectionnés
également sur la base de l'équivalence des versions francophones
et anglophones. Par la suite, nous avons donc considéré comme
équivalents (et donc sur une même échelle) les tests
francophones et anglophones.
|
|



