IV. Mise à l'échelle des tests 2005 et
2011
IV.1. Vérification des hypothqses de la mise
à l'échelle
Pour pouvoir comparer le niveau d'acquisition des
élève du Cameroun de 2005 (TEST PASEC 2005) à celui des
élèves de 2011 il a fallu mettre les deux test sur une même
échelle, par convention on prend la première année (2005)
comme référence.
Pour ce faire on a repris la procédure
développée dans le chapitre III.
Pour faciliter les calculs on a développé sur R
un programme qui permet, en un seul clic de donner les résultats,
partant ainsi de l'estimation des paramètres, jusqu'au calcul des scores
calibrés passant par la mise à l'échelle. Le programme est
donné en annexe III.
Nous avons comparé les résultats de notre
programme avec le package R Irtoys mis au point très récemment et
qui permet la mise en oeuvre d'un test equating.
Toutefois, il faut au préalable s'assurer de la
validité des hypothèses postulées auparavant.
1. le nombre d'items d'ancrage doivent correspondre à 20%
du nombre total d'items du test
2. les tests doivent mesurer les mêmes aptitudes
3. les tests doivent vérifier l'indépendance des
réponses aux items
4. les tests doivent être unidimensionnels
5. l'échantillon doit être de taille suffisante (au
moins 1800 élèves)
6. les items d'ancrage doivent être placés dans le
même ordre dans les deux tests
7. les items d'ancrage doivent être représentatifs
en contenu et en valeurs statistiques des deux tests
8. les deux tests contiennent le même nombre d'items
Voyons donc si nos tests vérifient bien les
différentes hypothèses.
Le test PASEC contient 42 items et le test 2011 contient 39
items. Ils ne sont pas tout à fait égaux en contenus car le test
2011 contient des items de production d'écrits mobilisant des
compétences supérieures et faisant appel à des questions
ouvertes à réponse longue.
De même, le test 2011 contient beaucoup de questions
ouvertes à réponse courte, alors que le test PASEC contient
principalement des QCM.
Pour pallier à cette situation, 6 items de production
d'écrits du test 2011 ont été supprimés, ainsi que
9 items du test PASEC sur la base des corrélations item-test et indices
de difficulté, ou fonctionnement différentié
anglophone-francophone.
On obtient ainsi deux sous test de 33 items chacun, qui
mesurent les mêmes habiletés (compréhension en lecture et
outils de la langue) et qui serviront à faire la mise à
l'échelle, sur la base de cinq items communs (soit 15% du test
total).
Les cinq items PASEC ont été choisis sur la base
de l'indice de difficulté (proche de 0.5), et surtout de
l'équivalence des versions francophones et anglophones des items tant
sur le plan linguistique que sur le plan psychométrique (pas de biais
d'items).
Les hypothèses 2, 7 et 8 sont donc
vérifiées.
L'hypothèse 3 d'indépendance des items est
également respectée par la construction des tests.
L'hypothèse 4 d'unidimensionnalité est
également vérifiée sur la base de la cohérence
interne des tests et des corrélations item-test mais également
par l'analyse factorielle (voir Monseur pour l'analyse des réponses aux
items des tests PASEC).
Ces deux hypothèses étant vérifiées,
la mise en oeuvre des modèles de réponse à l'item est
possible.
S'agissant de l'hypothèse 5, les échantillons
sont respectivement de 2361 élèves en 2005 et de 2553
élèves en 2011. Par contre, l'hypothèse 6 n'est pas
vérifiée, les items communs se situent au milieu du test 2011 et
dans diverses parties du test PASEC 2005.
Globalement, les sous-tests qui vont servir à la mise
à l'échelle respectent bien les différentes conditions,
bien que le nombre d'items d'ancrage soit assez faible.
Après comparaison des différents critères
tels que AIK, etc.., un modèle à deux paramètres s'ajuste
bien aux deux échantillons.
Les statistiques d'ajustement des items aux modèles
montrent que 7 items du test 2011 et 7 items du test 2005 ne suivent pas bien
le modèle.
Néanmoins, ces items seront conservés pour la mise
à l'échelle. IV.2. &KRiI
-GT-la-PptKRGT-GT-la-PIIT-E-l'pFKTllT
Il existe quatre méthodes permettant de mettre sur une
même échelle des tests comportant des items communs Davier (2011)
:
1. La méthode mean/mean se base sur les moyennes des
paramètres des items communs ;
2. La méthode mean/sigma se base sur les moyennes et les
écarts types des paramètres des items communs ;
3. La méthode Stocking-Lord ;
4. La méthode Haebara .
Les deux premières méthodes reposent sur
l'utilisation d'une transformation linéaire des paramètres des
items d'ancrage, tandis que les deux autres méthodes se basent sur une
minimisation de différences de carrés.
Nous allons utiliser la méthode N°2 qui peut
être facilement mise en oeuvre et qui fournit des estimations
raisonnables des différences d'habiletés des élèves
entre deux vagues d'évaluation.
Cette méthode sera mise en oeuvre sur Excel, puis sur R en
mettant au point un programme puis avec le package Irtoys5 mis au
point récemment.
Les courbes ci-dessous présentent les scores vrais
estimés en fonction du niveau d'habilité des
élèves. La courbe en vert est pour 2005, la courbe en rouge est
pour 2011.
5 On notera que le package Plink permet aussi la mise
à l'échelle mais s'avère compliqué à
paramétrer.
Graphique 8: le score vrai estimé de 2005 vs le
score vrai estimé de 2011
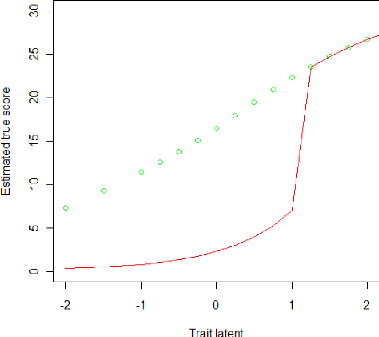
Comme la courbe rouge est globalement en dessous de la courbe
verte, cela signifie que le score vrai estimé a baissé
entre 2005 et 2011. Ainsi, on en conclut que le niveau d'acquisition
des élèves a globalement baissé; aussi, on remarque que
pour les élèves de niveau moyen, c'est-à-dire pour des
thêtas compris entre -1 et 1, la baisse est beaucoup plus importante
pendant que les forts se maintiennent à leur niveau.
La méthode mean/ sigma peut être mis en oeuvre en
plusieurs étapes grâce aux package ltm et irtoys sur le logiciel R
(Voir code en annexe III). On a mis sur
une même graphique les 3 courbes, en vert le <<
true score >> 2005, en bleu le << true score >> avec le
package irtoys, et en rouge le true score avec la méthode décrite
cidessous.
Graphique 9 : package Irtoys vs Résultats
produit avec notre programme R


Les résultats obtenus avec le package Irtoys convergent
avec les résultats produits avec notre programme sur R, à savoir
que le niveau des élèves a baissé entre 2005 et 2011.
Conclusion
| 


