II. Validation des postulats de base de TRI
Comme signaler précédemment, la TRI repose sur
trois hypothèses fondamentales à savoir l'indépendance
locale, l'unidimensionnalité et la monotonocité. Dans notre cas,
les items sont indépendant par construction, par conséquent il ne
s'agira, dans cette rubrique, que de vérifier la validité des
deux autres hypothèses.
II.1. Unidimensionnalité
Cette analyse portera sur deux graphiques représentants
les résultats d'une analyse en composante principale le premier
réalisé avec R et le deuxième avec
STATA ; tout deux convergent vers le même résultat
l'unidimensionnalité des items.
Reprenons le même exemple du test langue francophone
2011, Au regard des deux graphiques ci-dessous, on peut affirmer que les items
mesurent bien un seul trait latent.
Graphique 2 : analyse en composante principale (avec
R)

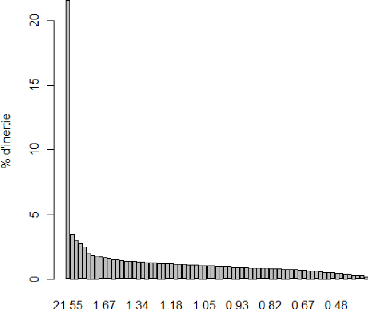
Pour réaliser cette procédure on utilise la
fonction « dudi.pca() » du package « ade4 ».Comme l'indique
le graphique ci-dessus, l'axe 1 explique 22,55% de l'inertie et l'axe 2 1,67%.
Il y a donc a priori une seule composante principale, donc le test est
unidimensionnel.
Figure 6: analyse en composante principale (avec
STATA)
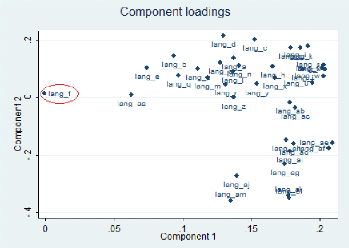
On voit bien que l'item « lang_f » » est proche du
point d'intersection des deux axes (0,0) donc ne contribue pas beaucoup
à l'inertie.
II.2. La monotonocité
Un modèle économétrique simple (le
modèle de Rach par exemple) permet d'avoir une représentation
graphique de la relation fonctionnelle entre le trait latent (l'habilité
de l'élève) et la probabilité de réussite à
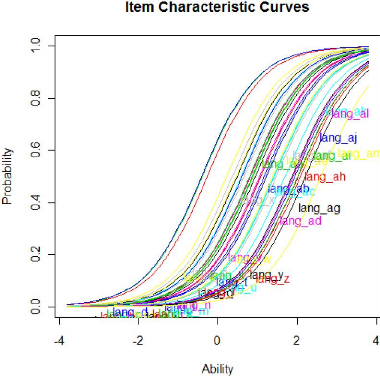
l'item. Comme nous pouvons le voir dans le graphique ci-dessous les CCI du test
de langue suivent une fonction monotone non décroissante.
Graphique 3: courbe caractéristique des items
du test langue francophone
(estimé selon le modèle de Rasch)
| 


