2.5. Test de cointégration
Dans cette partie, nous allons
expliciter deux approches de cointégration à savoir
l'approche en deux étapes d'Engle et Granger (1987) et la
cointégration multidimensionnelle de Johansen (1988).
2.5.1. Théorème de représentation
d'ENGLE et GRANGER (1987)
Soit la relation suivante :
Yt = a + bXt + et (2.32)
Si les deux variables Yt et Xt sont I (1)
alors, en général, la combinaison linéaire
Yt - a - bXt = et est également I (1). Cependant, il
est possible que et soit stationnaire
ou bien I (0). Pour qu'une telle éventualité se
réalise, il faudra que les trends entre les variables Yt et Xt soient
cointégrées et b est le paramètre de
cointégration. En d'autres termes, deux séries Yt et Xt sont
dites cointégrées si chacune d'entre elle est I (1)
et qu'il existe une combinaison linéaire telle que
Yt - a - bXt = et soit I (0).
et décrit les déviations de Yt et de Xt
par rapport à leurs sentiers d'équilibre respectifs.
Ce résidu est souvent qualifié d'erreur
d'équilibre. A partir du moment que et est stationnaire, les deux
séries temporelles Yt et Xt respectent une relation stable de
long terme. L'application de la technique de la cointégration
reviendrait dans
ces conditions à s'assurer de la
stationnarité des termes d'erreur d'équilibre. La
méthode employée par Engle et Granger (1987) repose
sur deux étapes :
· La première étape consiste à
estimer l'équation ou la régression de cointégrations
par la méthode des moindres carrées ordinaires (MCO) sachant que
Yt et Xt sont intégrées d'ordre 1. Cette
opération permettra d'extraire les résidus estimés ;
· La seconde étape sera consacrée à
tester la stationnarité des résidus dégagés de la
première ètape. Si ceux-ci sont stationnaires, les
variables figurant au niveau de la régression
susmentionnée sont cointégrées. Engle et Granger
préconisent pour ce faire, l'utilisation
du test de Dickey-Fuller augmenté (ADF).
Disposant de variables stationnaires en
différence première, on va chercher dans ce qui suit,
à identifier des variables d'équilibre de long terme
à partir de l'estimation de relations cointégrantes liant
le taux de change à ses déterminants fondamentaux.
Estimation par MCO
Comme première étape au test
de cointégration de Engle et Granger, on va procéder
à l'estimation par les moindres carrées ordinaires le
modèle monétaire (MM :
équation 2.20).
2.14.
LTCR = C + C1 LDIP + C2 LDDM + åt
(2.33)
Les résultats de l'estimation de
l'équation 2.33 sont reportés dans le tableau
Tableau 2.14 estimation du MM par
MCO
|
Parités
|
C
|
C1
|
C2
|
R2
|
DW
|
|
EURO/$
|
0.0375
|
0.5156
|
-0.2210
|
0.4013
|
0.0752
|
Les résultats des estimations du MM,
Durant la période (1990 : 01 - 2004 : 09),
par les moindres carrées ordinaires sont
satisfaisantes puisque les signes des coefficients sont conformes aux
prédictions de la théorie.
Par ailleurs, la lecture des résultats
révèle la présence conjointe d'un coefficient
de détermination assez faible (R2 =
0.4013) et d'une statistique de Durbin-Watson faible (DW = 0.0752) ce
qui illustre bien le cas d'une régression fallacieuse (ce
résultat est cohérent avec la « règle »
intuitive fournie par Granger et Newbold (1974) concernant la
présomption de régression fallacieuse). Ce
phénomène s'explique principalement par la non
stationnarité des variables sous-jacentes au modèle
monétaire.
Etude du résidu
Après l'estimation du modèle
par MCO, on va étudier dans ce qui suit les
propriétés statistiques du résidu dégagé
par la régression. Cette étude confirmera l'existence d'une
relation de cointégration entre les différentes variables du
modèle si
le résidu est stationnaire et l'infirmera dans le cas de
non stationnarité du résidu. Dans
ce but, on va commencer par jeter un oeil sur l'évolution
de ce résidu par la figure 2.2.
Figure 2.2 : graphique du
résidu
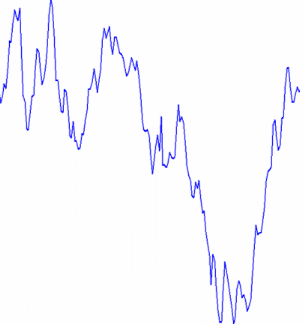
Figure 2.2 : graphique du
résidu
3
2
0
-1
-2
1990 1992 1994 1996 1998 2000 2002 2004
D'après l'examen de l'évolution
du résidu, on constate que le résidu est non
stationnaire qu'on va confirmer par le test de racine unitaire
d'ADF et de PP.
Les résultats de tests de
stationnarité d'ADF et PP sont reportés dans le tableau
2.15. Ces résultats confirment bien l'existence
de racine unitaire dans le résidu du modèle
étudié. Ceci infirme la présence de relation
de cointégration entre les différentes variables des
modèles.
Tableau 2.15 Test ADF et PP sur le
résidu
|
Variables
|
Test ADF
|
Test PP
|
|
Résidu
|
-1.4461
|
-1.09925
|
On conclut que les tests fondés sur
la méthode en deux étapes de Engle
et Granger (1987) conduisent à un rejet quasi
systématique des modèles théoriques (du fait de l'absence
de relation de cointégration).
Nos résultats rejoingnent ceux de Meese
(1986) et Boothe et Glassman (1987)
pour les modèles monétaires.
Plus récemment, en utilisant la
méthode de Johansen, MacDonal et Taylor (1993, 1994) mettent en
évidence plusieurs relations de cointégration, rendant une
certaine validité empirique à ces modèles.
| 


