Chapitre 2
Modèles de prédiction en Machine
Learning
2.1 Introduction
La durée de séjour hospitalier est sans doute un
facteur qui indique en quelques sortes la force et la viabilité d'un
système hospitalier. Cette prédiction a vu son essort depuis que
l'Intelligence Artificielle, spéciallement les Machines Learning sont
entrain de s'imposer dans la prise de décision dans presque tous les
domaines de la vie. Parfois, on ne sait pas distinguer ce qui est
intélligence artificielle, apprentissage automatique et
apprentissage profond.
Le but de ce chapitre est tout d'abord de présenter le
machine learning, son historique et ses champs d'application, en suite nous
mettrons au courant les differents modèles de prédiction de
machine learning, ainsi que la définition d'un modèle pertinant
et en fin, comprendre le rôle de ces modèles dans la
prédiction de DDS.
2.2 Intelligence Artificielle, Machine Learning et Apprentissage
Profond
Premièrement, nous devons définir clairement ce
dont nous parlons lorsqu'il est question d'IA. Que sont l'intelligence
artificielle, l'apprentissage automatique et l'apprentissage
20
profond ? Quels liens existent entre eux (figure 2.1) ?
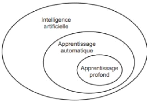
FIGURE 2.1 - Les relations entre l'intelligence artificielle,
l'apprentissage automatique et l'apprentissage profond [10]
2.2.1 Intelligence Artificielle : Artificial
Intelligent (AI)
L'intelligence artificielle est née dans les
années 50, quand une poignée de pionniers de l'informatique
naissante ont commencé à se demander si les ordinateurs
pouvaient
être conçus pour « penser » une
question dont nous continuons aujourd'hui d'explorer
les ramifications. Une
définition précise de ce domaine serait la suivante : c'est
l'effort d'automatisation des tâches intellectuelles normalement
effectuées par des humains [10].
L'intelligence artificielle est donc un domaine
général qui englobe l'apprentissage automatique et
l'apprentissage profond, mais qui comprend également de nombreuses
autres approches qui n'impliquent aucun apprentissage. Pendant très
longtemps, de nombreux experts ont cru qu'une intelligence artificielle
équivalente à celle de l'homme pouvait être atteinte en
faisant en sorte que les programmeurs fabriquent un ensemble suffisamment large
de règles explicites pour manipuler les connaissances. Cette approche
est connue sous le nom d'intelligence artificielle symbolique (symbolic AI), et
ce fut le paradigme dominant de l'IA des années 1950 à la fin des
années 1980. Elle a atteint son apogée pendant le boom des
systèmes experts (expert systems) dans les années 1980 [10].
Bien que l'IA symbolique se soit révélée
apte à résoudre des problèmes logiques bien
définis, tels que jouer aux échecs, elle s'est
avérée incapable de définir des règles explicites
pour résoudre des problèmes plus complexes et flous, tels que la
classification d'images, la reconnaissance de la parole et la traduction
linguistique. Une nouvelle approche est apparue, et elle a pris la place de
l'intelligence artificielle symbolique : c'est
l'apprentissage
21
automatique (machine learning) [10].
2.2.2 Apprentissage automatique : Machine
Learning
Dans l'Angleterre victorienne, Lady Ada Lovelace était
une amie et une collaboratrice de Charles Babbage, l'inventeur de la machine
analytique (Analytical Engine) : le premier ordinateur mécanique
polyvalent connu. Bien que visionnaire et très en avance sur son temps,
la machine analytique n'était pas conçue comme un ordinateur
polyvalent (general purpose computer) lorsqu'elle a été
pensée dans les années 1830 et 1840, car le concept de calcul
polyvalent n'avait pas encore été inventé. C'était
simplement un moyen d'utiliser des opérations mécaniques pour
automatiser certains calculs du domaine de l'analyse
mathématique d'où le nom de machine analytique.
En 1843, Ada Lovelace a ainsi
commenté l'invention : « le moteur
analytique n'a aucune prétention à être à l'origine
de quoi que ce soit. Il peut faire toutes les tâches dont nous savons
comment lui ordonner de les effectuer [...]. Son domaine de compétence
est de nous aider à rendre disponible ce que nous connaissons
déjà. » Le pionnier de l'IA, Alan Turing, a cité
cette remarque plus tard comme « l'objection de Lady Lovelace » dans
son article phare de 1950 appelé « Computing Machinery and
Intelligence » qui présentait le test de Turing ainsi que les
concepts clés qui façonneront plus tard l'IA. Turing citait Ada
Lovelace en se demandant si les ordinateurs polyvalents pourraient être
un jour capables d'apprendre et de faire preuve de créativité, et
il en vint à la conclusion qu'ils en seraient capables. L'apprentissage
automatique découle de cette question : un ordinateur pourrait-il aller
au-delà des « tâches dont nous savons comment lui ordonner de
les effectuer », et apprendre par lui-même comment effectuer une
tâche spécifique ? Un ordinateur pourrait-il nous surprendre ?
À la place de programmeurs élaborant à la main des
règles de traitement de données, un ordinateur pourrait-il
apprendre automatiquement ces règles par l'exposition aux données
?
Cette question ouvre la porte à un nouveau paradigme de
programmation. En programmation classique, le paradigme de l'IA symbolique,
l'homme saisit des règles (un programme) et des données à
traiter conformément à ces règles, et il en découle
des réponses en sortie. Avec l'apprentissage automatique, les humains
entrent des données,
22
ainsi que les réponses attendues à partir de ces
données, et ils obtiennent des règles en sortie. Ces
règles peuvent ensuite être appliquées à de
nouvelles données pour produire des réponses originales.
Un système d'apprentissage automatique est
entraîné plutôt qu'explicitement programmé. De
nombreux exemples pertinents pour une tâche lui sont
présentés. Puis il trouve dans ces exemples une structure
statistique qui lui permet à terme d'élaborer des règles
pour l'automatisation de la tâche. Par exemple, si vous souhaitez
automatiser l'étiquetage de vos photos de vacances, vous pouvez
présenter à un système d'apprentissage automatique de
nombreux exemples d'images déjà étiquetées par des
humains, et le système apprendra des règles statistiques pour
associer, à des images spécifiques, des étiquettes
spécifiques. Bien que l'apprentissage automatique n'ait commencé
à prospérer que dans les années 1990, il est rapidement
devenu le sous-domaine de l'IA le plus populaire et le plus performant. Cette
tendance est alimentée par la disponibilité de matériels
informatiques plus rapides et de plus grands ensembles de données.
L'apprentissage automatique est étroitement lié aux statistiques
mathématiques, mais il diffère des statistiques sur plusieurs
points importants. À la différence des statistiques,
l'apprentissage automatique traite généralement de vastes et
complexes ensembles de données (par exemple un ensemble de
données de millions d'images, chacune comprenant des dizaines de
milliers de pixels) pour lesquels une analyse statistique classique telle
qu'une analyse bayésienne serait impossible à mettre en oeuvre.
En conséquence, l'apprentissage automatique, et en particulier
l'apprentissage profond : Deep Learning,
présente relativement peu de théorie mathématique
peut-être trop
peu et est axé sur l'ingénierie. C'est une
discipline pratique dans laquelle les idées sont
plus souvent
prouvées empiriquement que théoriquement.
2.2.3 Apprentissage des représentations à
partir de données
Pour définir l'apprentissage profond (deep learning en
anglais) et comprendre la différence entre l'apprentissage profond et
les autres approches d'apprentissage automatique, nous devons d'abord avoir une
idée du fonctionnement des algorithmes d'apprentissage automatique. Nous
venons juste d'énoncer que l'apprentissage automatique découvre
des règles permettant d'exécuter une tâche de traitement de
données, lorsque lui sont fournis
23
des exemples de résultats attendus. Pour faire de
l'apprentissage automatique, nous avons donc besoin de trois choses :
- des points de données d'entrée (input data
points) par exemple, si la tâche est
la reconnaissance vocale, ces
points de données peuvent être des fichiers audio de personnes qui
parlent ; si la tâche est l'étiquetage d'images, ces points de
données peuvent être des images ; si c'est dans le cas de ce
papier, on aura donc besoin de données d'entrées de la
patiente.
- des exemples de sortie attendue (expected output) dans une
tâche de reconnaissance vocale, il peut s'agir de transcriptions de
fichiers sonores générés par l'homme ; dans une
tâche d'étiquetage d'images, les sorties attendues peuvent
être des étiquettes telles que « chien », « chat
», etc. ; dans une tâche de séjour hospitalier les output
sont donc des séjours moyens de chacune des patientes.
- un moyen de mesurer la performance de l'algorithme c'est un
élément nécessaire pour déterminer la distance, au
sens mathématique, entre la sortie effective de l'algorithme et la
sortie attendue ; la mesure est utilisée comme un signal de retour
(feedback) pour ajuster le fonctionnement de l'algorithme ; cette étape
d'ajustement est ce que nous appelons l'apprentissage.
Un modèle d'apprentissage automatique transforme ses
données d'entrée en sorties qui ont un sens, c'est un processus
qui est « appris » à partir de l'exposition à des
exemples connus d'entrées et de sorties. Par conséquent, le
problème central de l'apprentissage automatique et de l'apprentissage
profond est de transformer de manière utile les données : en
d'autres termes, d'apprendre des représentations utiles des
données d'entrée disponibles
des représentations qui nous rapprochent du
résultat attendu. Avant d'aller plus loin : qu'est-ce qu'une
représentation ? Fondamentalement, c'est une façon
différente
de considérer les données de représenter
ou d'encoder les données. Les modèles
d'apprentissage
automatique ont pour but de trouver des représentations
appropriées pour
leurs données d'entrée des transformations de
données qui les rendent plus adaptées à
la tâche
à accomplir, telle que par exemple une tâche de classification.
Techniquement, voici ce qu'est l'apprentissage automatique :
c'est la recherche de représentations utiles de certaines données
d'entrée, dans un espace des possibilités
prédéfini, en s'appuyant sur un signal de retour. Cette
idée simple permet de résoudre un
24
très large éventail de tâches
intellectuelles, de la reconnaissance automatique de la parole à la
conduite automobile autonome.
Disons, ce qui est profond de
l'apprentissage profond est donc une nouvelle approche de
l'apprentissage des représentations à partir des données
qui met l'accent sur l'apprentissage de couches (layers) successives de
représentations qui sont de plus en plus significatives.
L'adjectif « profond » de l'apprentissage profond ne
fait pas référence à une forme de compréhension
plus approfondie réalisée par l'approche mise en oeuvre ; il
représente plutôt l'idée de couches successives de
représentations.
2.3 Les apprentissages en Machine Learning 2.3.1
Introduction
Dans cette section, nous allons voir quelques algorithmes de
prédictions de Machine Learning tantôt en apprentissange
supervisé, en apprentissage non supervisé ou en apprentissage par
renforcement.
Au delà de ces différents apprentissages, il
existe des algorithmes utiliés dans l'un ou l'autre apprentissage. Ces
modèles au finish nous serviront en grande partie dans la conception du
modèle de prédiction en Gynécologie qui fera l'objet de ce
mémoire.
Parlons d'abord de ce qui est de l'apprentissage
supervisé, l'apprentissage non supervisé et l'apprentissage par
renforcement ([19] et[25]).
2.3.2 Apprentissage supervisé
L'apprentissage supervisé est fait en utilisant une
vérité, c'est-à-dire qu'on a une connaissance
préalable de ce que les valeurs de sortie pour nos échantillons
devraient être. Par conséquent, le but de ce type d'apprentissage
est d'apprendre une fonction qui, compte tenu d'un échantillon de
données et de résultats souhaités, se rapproche le mieux
de la relation entre les entrées et les sorties observables dans les
données. La figure 2.2 est un exemple d'un modèle de traitement
de données en apprentissage supervisé.
Dans l'apprentissage supervisé, on a deux types
d'algorithmes :
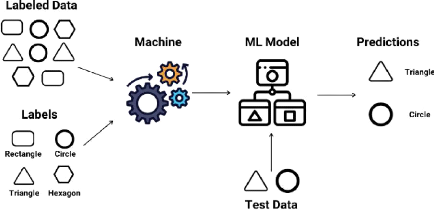
25
FIGURE 2.2 - Modèle de traitement de données en
apprentissage supervisé [1]
- Les algorithmes de régression, qui cherchent à
prédire une valeur continue, une quantité.
- Les algorithmes de classification, qui cherchent à
prédire une classe/catégorie.
2.3.3 Apprentissage non supervisé
Dans l'apprentissage non supervisé (clustering en
anglais), l'ensemble de données est divisé en sous-groupes
homogènes pour obtenir une représentation simplifiée de
l'ensemble de départ [19]. Les algorithmes d'apprentissage automatique
non supervisés sont utilisés lorsque l'information
utilisée pour entraîner le modèle n'est ni
classifiée ni étiquetée. Le modèle en question
étudie ses données d'entrainement dans le but de déduire
une fonction pour décrire une structure cachée à partir
des données (figure 2.3). À aucun moment le système ne
connaît la sortie correcte avec certitude. Au lieu de cela, il tire des
inférences des ensembles de données quant à ce que la
sortie devrait être. [1].
Les algorithmes de ce type d'apprentissage peuvent être
utilisés pour trois types en problèmes.
- Association : un problème où
on désire découvrir des règles qui décrivent de
grandes portions de ses données. Par exemple, dans un contexte d'une
étude de
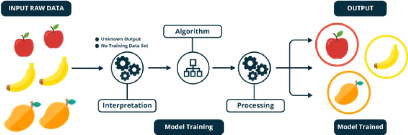
26
27
FIGURE 2.3 - Modèle de traitement de données en
apprentissage non supervisé [1]
comportement d'achat d'un groupe de clients, les personnes qui
achètent tel produit ont également tendance à acheter un
autre produit spécifique.
- Regroupement : un problème où
on veut découvrir les groupements inhérents
aux données, comme le regroupement des clients par le
comportement d'achat. - La réduction de dimension : on
vise à réduire le nombre de variables à prendre
en compte dans l'analyse.
2.3.4 Apprentissage semi-supervisé
Ce type d'algorithme est la combinaison entre l'apprentissage
supervisé et l'apprentissage non supervisé. Ces algorithmes sont
capables d'apprendre à partir d'ensembles de données
partiellement étiquetées [19].
2.3.5 Apprentissage par renforcement
L'apprentissage par renforcement est une méthode qui
consiste à optimiser de manière itérative un algorithme
uniquement à partir des actions qu'il entreprend et de la réponse
associée de l'environnement dans lequel il évolue (figure
2.4).
Cette méthode permet aux machines et aux agents de
déterminer automatiquement le comportement idéal dans un contexte
spécifique pour maximiser ses performances. Une simple
rétroaction de récompense, connue sous le nom de signal de
renforcement, est
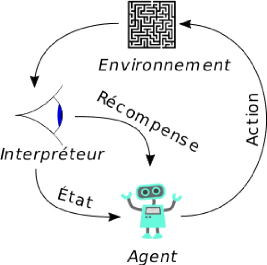
FIGURE 2.4 - Modèle de traitement de données en
apprentissage par renforcement
nécessaire pour que l'agent apprenne quelle action est la
meilleure.
La plus part des problèmes de la DDS utilisent les
algorithmes de l'apprentissage supervisé car, avant d'étudier la
DDS d'un patient, il faut donc savoir pour les précédents, leurs
DDS et ainsi, les faire appliquer au nouveau modèle.
2.4 Algorithmes de l'apprentissage automatique
Dans la partie suivante nous allons parcourir quelques
algorithmes en apprentissage supervisé car, sont eux qui nous serviront
dans la suite de ce travail.
Pour résoudre un problème en apprentissage
supervisé, on fait recours à plusieurs méthodes qui sont
applicables dans plusieurs domaines [1]. Dans la suite, nous allons essayer de
voir certains algorithmes en apprentissage automatique. Précisons que la
liste n'est pas exhaustive mais nous allons juste essayer de présenter
ici quelques modèles mais pas les tous.
28
2.4.1 Régression linéaire
La régression linéaire est l'une des
méthodes de prédiction en ML. Elle utilise des variables
quantitatives et l'idée plus générale ici est juste
d'exprimer les variables par une fonction f(x).
L'un de ses principaux mérites est de fournir une
illustration pédagogique élémentaire des différents
concepts du ML. Il suppose que la fonction de prédiction f qui
lie les variables prédictives x1, ..., xp
à la variable cible a la forme :
f(x) = a0x0 +
a1x1 + a2x2... +
apxp = a x x + b (2.1)
La régression linéaire est utilisée pour
l'estimation de certaines tendances en économétrie et dans le
marketing lorsqu'on a des raisons de penser qu'il existe une relation
linéaire entre la variable explicative et la cible. Établir la
relation entre l'augmentation du prix d'un produit et sa demande,
évaluer l'impact d'une campagne publicitaire en fonction des frais
engagés sont des exemples d'utilisation [15].
L' apprentissage du modèle consiste en l'occurrence
à calculer les coefficients ai qui minimisent les erreurs de
prédiction sur un jeu de données d'apprentissage. Le plus souvent
l'erreur est définie comme la somme des carrés des écarts
entre les valeurs prédites f(x(i))
et les valeurs observées yi. On parle à ce
titre de méthode des moindres carrés. Le
carré ici des erreurs nous permet de ne pas avoir des valeurs
négatives qui pourraient probablement se simplifier et ainsi faire
penser au concepteur du modèle que nous est correct or il y a des
valeurs érronées.
Erreur et la fonction coût
Un modèle de ML le plus souhaité, est celui qui
minimise l'erreur. C'est ainsi que dans la conception d'un algorithme de
Machine Learning, on cherche toujours à prendre le modèle qui a
moins d'erreurs.
En effet, pour chaque point xi, l'erreur unitaire
pour ce point xi est donné par la différence entre la
valeur prédite et la vraie valeur. Pour se rassurer que cette valeur
sera positive pour que l'équation 2.3 ne soit pas nulle, on
élève cette difference au carré :
(f(xi) - yi)2.
L'erreur unitaire étant déjà
définie, faisons une sommation de ces erreurs pour plusieurs points.
L'équation 2.2 donne [12] :
Xm (f(xi) -
yi)2. (2.2)
i=1
La fonction coût (équation 2.3) est
définie en normant cette somme de l'équation 2.2 par le nombre
m de points dans la base [12] :
m
1
J(è0, è1) = 2
X (f(xi) - yi)2 (2.3)
m i=1
29
Il existe aussi des modèles linéaires
généralisés qui se basent sur des lois de
probabilité. Les modèles linéaires
généralisés (GLM) étendent les modèles
linéaires de deux manières [2]. Premièrement, les valeurs
prédites y sont liés à une combinaison
linéaire des variables d'entrée x via une fonction de
lien inverse. Deuxièmement, la fonction de perte au carré est
remplacée par la déviance unitaire d'une distribution dans la
famille exponentielle (ou plus précisément, un modèle de
dispersion exponentielle reproductive (EDM).On fait alors le choix d'une
distribution statistique à faire. Ceci est guidé par la
caractéristique de données qu'on a [2] :
- Si les valeurs cibles y sont des nombres (valeur
entière non négative) ou des fréquences relatives (non
négatives), vous pouvez utiliser une distribution de Poisson avec un
lien logarithmique.
- Si les valeurs cibles y sont positives et
asymétriques, vous pouvez essayer une distribution Gamma avec un lien de
journal.
- Si les valeurs cibles y semblent avoir une queue
plus lourde qu'une distribution Gamma, vous pouvez essayer une distribution
gaussienne inverse (ou des puissances de variance encore plus
élevées de la famille Tweedie).
- Si les valeurs cibles y sont des
probabilités, vous pouvez utiliser la distribution de Bernoulli. La
distribution de Bernoulli avec un lien logit peut être utilisée
pour la classification binaire. La distribution catégorielle avec un
lien softmax peut être utilisée pour la classification
multiclasse.
30
D'après l'équation 2.1, nous pouvons encore
définir par 'q la DDS prédite à un moment
t [22]. Cette équation devient donc :
'17 = a0 + Xp
aixi (2.4)
i=1
2.4.2 Les k plus proches voisins
Le modèle des k plus proches voisins (KNN pour
k Nearest Neighbors) est un des modèles
prédictifs les plus simples. Il ne fait aucune hypthèse
mathématique et ne demande pas non plus toute une litanie des choses. Il
nécessite très peu de choses [15] :
- une notion de distance;
- et l'hypothèse que des points proches les uns des
autres sont similaires.
L'opérateur de distance le plus souvent utilisé
est la distance Euclidienne, cependant, en fonction du problème, on peut
encore utiliser d'autres distances [26], etc
Principe de l'algorithme
On suppose que l'ensemble E contient n
données labellisées et u , une autre donnée
n'appartenant pas à E qui ne possède pas de label. Soit
d une fonction qui renvoie la distance (qui reste à choisir)
entre la donnée u et une donnée quelconque appartenant
à E. Soit un entier k inférieur ou égal
à n [8]. Le principe de l'algorithme de k-plus proches voisins
est le suivant [3] et [8] :
- On calcule les distances entre la donnée u
et chaque donnée appartenant à E à l'aide de
la fonction d.
- On retient les k données du jeu de
données E les plus proches de u, c'est-à-dire,
les données déjà classifiées qui ont une distance
d la plus proche avec la nouvelle donnée entrée.
- On attribue à u la classe qui est la plus
fréquente parmi les k données les plus proches.
Les distances utilisées [3]
Les distances les plus souvent utilisées ici sont les
distances euclidienne et Manhattan.
1. Distance euclidienne
La distance Euclidienne est la distance utilisée pour
calculer la distance entre deux points. La distance Euclidienne d
entre les points A et B est donnée par la
relation suivante :
|
d(A, B) =
|
v u u Xn
tk=1
|
(yk -
xk)2. (2.5)
|
31
2. Distance Manhattan d
La distance de Manhattan est nommée ainsi car elle
permet de mesurer la distance parcourue entre deux points par une voiture dans
une ville où les rues sont agencées selon un quadrillage.
La distance de Manhattan d entre deux données
A et B est donnée par la relation suivante :
d(A,B) = Xn |
yk - xk |.
(2.6)
k=1
2.4.3 Les arbres de décision
Les arbres de décision sont des
modèles de ML supervisés et non paramétriques
extrêmement flexibles. Ils sont utilisables aussi bien pour la
classification que pour la régression. Nous décrirons ici
brièvement les principes utilisés pour la classification. Les
arbres de décision utilisent des méthodes purement algorithmiques
qui ne reposent sur aucun modèle probabiliste. L' idée de base
consiste à classer une observation au moyen d'une succession de
questions (ou critères de segmentation) concernant les valeurs des
variables prédictives Xi de cette observation.
Chaque question est représentée par un noeud d'un arbre de
décision. Chaque branche sortante du noeud correspond à une
réponse possible à la question posée. La classe de la
variable cible est alors déterminée par la feuille (ou noeud
terminal) dans laquelle parvient l'observation à l'issue de la suite de
questions [23].
Un modèle de Machine Learning comprend trois sortes de
noeuds [16] : les racines, les noeuds intermédiaires et les
branches. Deux noeuds sont reliés par des branches. La
figure 2.5 illustre ces diffentes parties d'un arbre de décision. Selon
la figure 2.5, on constate que la racine de cet arbre est
x0, les noeuds intermédiaires sont
x2, x3 et
x4. Par

32
FIGURE 2.5 - Exemple d'un arbre avec ses differentes parties
[16]
contre, les branches sont x1, x5;
x6, x7 et x8. On comprend dans ce sens que l'arbre
de décision n'est rien autre qu'une suite de questions où les
réponses constituent des branches et des feuilles.
La question de la profondeur de l'arbre qu'il faut retenir est
délicate et est directement liée au problème du
surapprentissage. Exiger que toutes les observations soient parfaitement
rangées peut rapidement mener au surapprentissage. Pour cette raison on
décide généralement de ne plus rajouter de noeuds lorsque
la profondeur de l'arbre excède un certain seuil, qui caractérise
la complexité maximale de l'arbre de décision, ou lorsque le
nombre d'observations par feuille est trop faible pour être
représentatif des différentes classes (on parle de
pré-élagage). On pratique aussi des opérations
d'élagage a posteriori (prunning) sur des arbres dont les feuilles sont
homogènes en utilisant un jeu de données distinct (prunning set)
de celui qui a permis la construction de l'arbre original [23].
Une fois l'arbre construit à partir des données
d'apprentissage, on peut prédire un nouveau cas en le
faisant descendre le long de l'arbre, jusqu'à une feuille.
Comme la feuille correspond à une classe, l'exemple sera
prédit comme faisant partie de cette classe [26].
Les arbres de décisions interviennent par ailleurs
comme brique de base de l'algorithme plus sophistiqué des forêts
aléatoires que nous présenterons au paragraphe suivant.
33
Quoi que l'arbre de décision soit un algorithme
important en prédiction, elle présente
aussi quelques faiblesses comme nous pouvons le lire selon [26]
:
- C'est un algorithme Glouton, sans backtrack (sans retracer ou
trace arrière).
- Transposables en règles avec des règles ayant des
attributs communs, en particulier
l'attribut utilisé à la racine.
- Présentent des difficultés avec les concepts
disjonctifs.
- Etc.
Aspect mathématiques
Dans cette partie, nous allons voir quelques fonctions
mathématiques utiles pour un arbre de décision. L'algorithme
utilise l'entropie (c'est une théorie tirant ses origines dans la
théorie de l'information. L'entropie en statistique designe le
désordre qui règne dans une population. La constuction de l'arbre
visera à minimiser ce bruit [12]) et le gain d'information comme
fonctions [6].
Etant donné un ensemble C de données
labélisées +, - et p la population totale,
l'entropie sur C de l'ensemble de données S est
donnée par l'équation 2.7
Entropie(C) = X
(-Pcilog2Pci)
(2.7)
ciEC
où Pci =
|Ci|
|S| représente une
probabilité de l'eventualité ci.
L'entropie étant déjà minimisée,
l'étape critialle est de savoir quel attribut testé en premier
(on choisira l'attribut qui maximisera le gain d'information ou, son
équivalent : qui minimisera l'entropie [6] [12] ). Il faut
connaître la notion de gain d'information. Le gain est défini par
un ensemble d'exemples et par un attribut. L'équation 2.8
formulée va donc servir à calculer ce que cet attribut apporte au
désordre de l'ensemble. Plus un attribut contribue au désordre,
plus il est important de le tester pour séparer l'ensemble en plus
petits sous-ensembles ayant une entropie moins élevée [6].
|
Gain(S, A) = Entropie(S) - X
cEvaleur(A)
|
| Sv |
| S | x Entropie(Sv)
(2.8)
|
Les arbres de décisions interviennent par ailleurs comme
éléments de base de l'algorithme
34
plus sophistiqué des forêts aléatoires que
nous présenterons au paragraphe suivant.
2.4.4 Les forêts aléatoires
Il est connu qu'une forêt est un ensemble de plusieurs
arbres (figure 2.6). Les forêts aléatoires sont donc un ensemble
de plusieurs arbres de décisions.
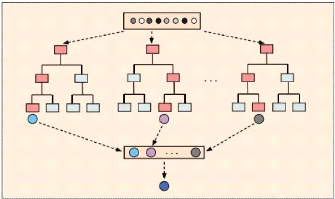
FIGURE 2.6 - Généralisation du modèle
prédictif Forêt aléatoire [16]
Prenons l'exemple suivant : imaginez-vous, vous vous
rendez à l'hôpital pour le CPN et d'un coût, un
médecin vous annonce que vous allez subir une opération (la
prémière après sept naissances d'avant.) Parfois vous
n'allez pas vous imaginer que cela soit possible. Il vous faut donc un
récours vers un autre médecin car vous supposez que
celui-là n'est pas soit à la hauteur de sa tâche.
[12]
Comme pour l'algorithme de l'arbre de décision, quoi
qu'il y a un seul arbre, mais à l'intérieur de ce dernier sont
groupés plusieurs autres questionnement qui permettent de bien
répondre à une certaine question. L'ensemble de ces portions
d'arbre à l'intérieur d'un arbre constituent pour ce faire un
algorithme appelé forêt aléatoire (Random Forest en
anglais) [12].
Origine des forêts aléatoires
[12]
On doit les random forests au fantastique Leo Breiman,
éminent statisticien américain connu pour ses travaux sur les
arbres décisionnels et sur la méthode CART, introduite
35
précédemment. Lui-même avait parfaitement
conscience du défaut majeur d'un arbre de décision : sa
performance est trop fortement dépendante de l'échantillon de
départ. De plus, on peut s'attendre à ce que l'ajout de quelques
nouvelles données dans la base d'apprentissage (ce qui est une bonne
nouvelle en soit !) ne modifie pas drastiquement le modèle, qu'il le
modifie de façon marginale pour l'améliorer. Ce n'est pas le cas
avec un arbre de décision, dont la topologie peut totalement changer
avec l'ajout de quelques observations supplémentaires. Plutôt que
de lutter contre ces défauts des arbres de décisions, Breiman a
eu l'idée géniale d'utiliser plusieurs arbres pour faire des...
forêts d'arbres ! Vous avez compris le forest dans random forest. Et
random alors ? Pour éviter de se retrouver avec des arbres égaux,
il donne à chaque arbre une vision parcellaire du problème, tant
sur les observations en entrée que sur les variables à utiliser.
Ce double échantillonnage est tout simplement tiré
aléatoirement. Notons que l'assemblage d'arbres de décision
construits sur la base d'un tirage aléatoire parmi les observations
constitue déjà un algorithme à part entière connu
sous le nom de tree bagging. Les random forests ajoutent au tree bagging un
échantillonnage sur les variables du problème, qu'on appelle
feature sampling. On retiendra que :
Random forest = tree
bagging + feature sampling
Avant d'entrer dans le détail de son fonctionnement,
notons enfin que l'on retrouve dans le random forest la polyvalence des arbres
de décision. En effet, on peut les utiliser :
- en classification, le résultat final étant obtenu
en faisant « voter » chaque arbre ;
- en régression, en moyennant le résultat des
arbres.
Le but de l'algorithme des forêts aléatoires est
de conserver la plupart des atouts des arbres de décision tout en
éliminant leurs inconvénients, en particulier leur
vulnérabilité au surapprentissage et la complexité des
opérations d'élagage. C'est un algorithme de classification ou de
régression non paramétrique qui s'avère à la fois
très fléxible et très robuste.
L' algorithme des forêts aléatoires repose sur trois
idées principales :
1. À partir d'un échantillon initial de N
observations (x(1), . . .
x(n)), dont chacune est décrite au moyen de
p variables prédictives, on crée « artificiellement
» B nouveaux échantillons de même taille N
par tirage avec remise. On appelle cette technique
36
le bootstrap. Grâce à ces B
échantillons, on entraîne alors B arbres de
décisions différents.
2. Parmi les p variables prédictives
disponibles pour effectuer la segmentation associée au noeud d'un arbre,
on n'en utilise qu'un nombre in < p choisies « au hasard
». Celles-ci sont alors utilisées pour effectuer la meilleure
segmentation possible.
3. L' algorithme combine plusieurs algorithmes « faibles
», en l'occurrence les B arbres de décisions, pour en
constituer un plus puissant en procédant par vote. Concrètement,
lors qu'il s'agit de classer une nouvelle observation x, on la fait
passer par les B arbres et l'on sélectionne la classe
majoritaire parmi les B prédictions. C'est un exemple d'une
méthode d'ensemble.
Le nombre B d'arbres s'échelonne
généralement entre quelques centaines et quelques milliers selon
la taille des données d'apprentissage. Le choix du nombre in de
variables à retenir à chaque noeud est le résultat d'un
compromis. Il a été démontré que les
prédictions d'une forêt aléatoire sont d'autant plus
précises que les arbres individuels qui la composent sont
prédictifs et que les corrélations entre prédictions de
deux arbres différents sont faibles. Augmenter le nombre in de
variables augmente la qualité de prédiction des arbres
individuels mais accroît aussi les corrélations entre arbres. Une
valeur in de l'ordre de /p constitue un bon compromis
[23].
2.4.5 Les réseaux de neurones
artificiels
Les réseaux de neurones artificiels sont
utilisés tantôt dans plusieurs disciplines mais ne constituent pas
en quelques sortes eux mêmes une discipline [27]. Un réseau de
neurone artificiel (parfois simplement réseau de neurones) est un
modèle de prédiction qui met en exergue le fonctionnement du
cerveau. Le cerveau ici considéré est une collection de neurones
connectés les uns aux autres. Chaque neurone examine les sorties des
autres neurones, qui deviennent ses entrées, effectue un calcul, puis se
déclenche ou pas [15]. La figure 2.7 est un exemple illustratif d'un
réseau de neurones.
Les réseaux de neurones résolvent nombreux
problèmes tels que la réconnaissance de l'écriture, la
réconnaissance faciale [25],[15], voire même la fonction du
système nerveu central [24].
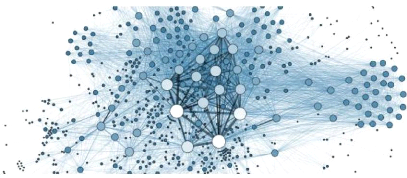
37
FIGURE 2.7 - Réseau de neurones [25]
Définition 2.1 Les réseaux
de neurones artificiels sont des réseaux fortement connectés de
processeurs élémentaires fonctionnant en parallèle. Chaque
processeur élémentaire calcule une sortie unique sur la base des
informations qu'il reçoit. Toute structure hiérarchique de
réseaux est évidemment un réseau.
Cependant, développer un réseau de neurones
à moindre coût est l'appanage de [25] : - Un Dataset beaucoup plus
grand (des millions de données)
- Un temps d'apprentissage plus long (parfois plusieurs
jours)
- Une plus grande puissance de calcul.
Pour dépasser ces challenges, les chercheurs dans le
domaine ont développés des variantes du Gradient Descent ainsi
que d'autres techniques pour calculer plus rapidement les
dérivées sur des millions de données. Parmi ces solutions
on trouve [25] :
- Mini-Batch Gradient Descent : Technique
pour laquelle le Dataset est fragmenté en petits lots pour simplifier le
calcul du gradient à chaque itération.
- Batch Normalization : Mettre à la
même échelle toutes les variables d'entrée et de sortie
internes au Réseau de Neurone pour éviter d'avoir des calculs de
gradients extrêmes.
- Distributed Deep Learning : Utilisation du
Cloud pour diviser le travail et le confier à plusieurs
machines.
Historique [27]
- 1890 : W. James, célèbre psychologue
américain introduit le concept de mémoire associative, et propose
ce qui deviendra une loi de fonctionnement pour l'apprentissage sur les
réseaux de neurones connue plus tard sous le nom de loi de Hebb.
- 1943 : J. Mc Culloch et W. Pitts laissent leurs noms
à une modélisation du neurone biologique (un neurone au
comportement binaire). Ce sont les premiers à montrer que des
réseaux de neurones formels simples peuvent réaliser des
fonctions logiques, arithmétiques et symboliques complexes (tout au
moins au niveau théorique).
- 1949 : D. Hebb, physiologiste américain explique le
conditionnement chez l'animal par les propriétés des neurones
eux-mêmes. Ainsi, un conditionnement de type pavlovien tel que, nourrir
tous les jours à la même heure un chien, entraîne chez cet
animal la sécrétion de salive à cette heure précise
même en l'absence de nourriture. La loi de modification des
propriétés des connexions entre neurones qu'il propose explique
en partie ce type de résultats expérimentaux.
Comment comprendre un réseau de neurones
?
La réponse à cette question viendra à l'aide
de l'exemple sur la figure 2.8. Sur cette
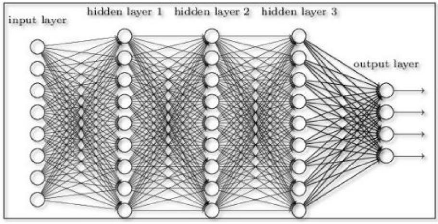
FIGURE 2.8 - Réseau de neurones à plusieurs
neurones [25]
38
39
figure, on remarque à gauche des entrées
appelées input layers et à gauche des sorties
appelées Output layers. Les petits ronds sont
appelés les neurones et représentent des fonctions d'activation
[25].
Ils sont classés suivant le nombre de neurones de chaque
réseau.
Réseau de Neurone à 1 Neurone : Le
perceptron
Le réseau de Neurones le plus simple qui existe porte
le nom de perceptron. Il est identique à la
Régression Logistique de la section précedente.
Les entrées du neurone sont les x
multipliées par des paramètres c à
apprendre. Il existe deux étapes pour le calcul d'un réseau de
neurone d'abord, un calcul linéaire par la somme de toutes les
entrées et le calcul de la fonction d'activation ou la fonction
logistique [25].
On utilise souvent d'autres fonctions d'activation que la
fonction sigmoïde pour simplifier le calcul du gradient et ainsi obtenir
des cycles d'apprentissage plus rapides [25] :
- La fonction tangente hyperbolique tanh(z)
- La fonction Relu(z)
Réseaux à plusieurs neurones : le Deep
Learning
Cette méthode se fait en étapes en liant plusieurs
perceptrons [25] :
- On réunit les neurones en colonne (on dit qu'on les
réunit en couche, en layer). Au sein de leur colonne, les neurones ne
sont pas connectés entre eux.
- On connecte toutes les sorties des neurones d'une colonne
à gauche aux entrées de tous les neurones de la colonne de droite
qui suit.
On peut ainsi construire un réseau avec autant de
couches et de neurones que l'on veut. Plus il y a de couches,
plus on dit que le réseau est profond (deep)
et plus le modèle devient riche, mais aussi
difficile à entraîner. C'est ça, le
Deep Learning [25].
Les réseaux de neurones entrent dans la
catégorie des modèles non linéaires en
leurs paramètres. La forme la plus courante de réseau de neurones
statique est une extension
simple de l'équation [14] :
g(x,w) = Xp w f (x,w')
(2.9)
=1
où les fonctions f (x, w') ,
appelées "neurones", sont des fonctions paramètrées qui
seront définies dans la suite.
La fonction f peut être
paramétrée de manière quelconque. Deux types de
paramétrage sont fréquemment utilisés [14] :
- les paramètres sont attachés aux variables du
neurone : la sortie du neurone est une fonction non linéaire d'une
combinaison des variables {x } pondérées par les
paramètres {w }, qui sont alors souvent désignés
sous le nom de « poids » ou, en raison de l'inspiration biologique
des réseaux de neurones, « poids synaptiques ».
Conformément à l'usage (également inspiré par la
biologie), cette combinaison linéaire sera appelée «
potentiel » dans tout cet ouvrage. Le potentiel v le plus
fréquemment utilisé est la somme pondérée, à
laquelle s'ajoute un terme constant ou « biais » :
v = wo + Xn w x (2.10)
=1
La fonction f est appelée fonction
d'activation.
- les paramètres sont attachés à la
non-linéarité du neurone : ils interviennent directement dans la
fonction f ; cette dernière peut être une fonction
radiale ou RBF (en anglais Radial Basis Function), ou encore une ondelette ; la
première tire son origine de la théorie de l'approximation, la
seconde de la théorie du signal . Par exemple, la sortie d'un neurone
RBF à non-linéarité gaussienne a pour équation :
2w2 n+1
Pn =1(x - w )2
y = exp(-
) (2.11)
40
2.5 Pertinence d'un modèle de
prédiction
Comme vu dans les chapitres précedents, il existre
plusieurs algorithme de prédiction en apprentissage automatique. Mais la
question qui reste toujours en jachère est celle de savoir si
réellement toutes ces méthodes ont les mêmes chances de
prédiction. C'est dans cette
perpective que dans cette section, nous allons essayer de voir
comment on peut parvenir à faire un choix des algorithmes à
maintenir pour la prédiction en Machine Learning. Nous allons parler de
quelques mesures d'estimation des algorithmes de regression [2].
2.5.1 Score R2,
coefficient de détermination
l représente la proportion de variance (de y)
qui a été expliquée par le variables indépendantes
dans le modèle. Il fournit une indication de la bonté de et donc
une mesure de la probabilité que les échantillons non vus soient
prédit par le modèle, à travers la proportion de variance
expliquée.
Étant donné que cette variance dépend de
l'ensemble de données, peut ne pas être significativement
comparable dans différents ensembles de données. Le meilleur
score possible est de 1,0 et il peut être négatif (parce que le
modèle peut être arbitrairement pire). Ceci veut dire que lorsque
le modèle coefficient de détermination est nul, inférieur
à zéro ceci s'explique en disant que quand la variable x
croit d'une valeur quelconque, la variable y décroit.
La formule 2.12 nous permet de calculer ce
coéfficient.
P(y -
ypred)2
R2 = 1
(2.12)
P(y -
moyenne(y))2
|
1
MAE =
n
|
n-1X
i=0
|
| yi - yi pred
(2.13)
|
41
2.5.2 Erreur absolue moyenne
La fonction calcule la moyenne absolue erreur, un risque
métrique correspondant à la valeur attendue de la perte d'erreur
absolue ou de la perte -norm.
Si est la valeur prédite du -ième
échantillon, et est la valeur vraie correspondante, alors l'erreur
absolue moyenne (MAE) estimé sur est défini comme suit :
2.5.3 Erreur quadratique moyenne
La fonction calcule le carré moyen erreur, un risque
métrique correspondant à la valeur attendue de l'erreur au
carré (quadratique) ou perte.
Si est la valeur prédite du -ième
échantillon, et est la valeur vraie correspondante, alors l'erreur
quadratique moyenne (MSE) estimé sur est défini comme suit :
|
1
MSE = n
|
n-1X
i=0
|
(yi - yi
pred)2 (2.14)
|
42
Il existe plusieurs autres mesures de performences d'un
modèle de regression, mais dans le cadre de ce travail, nous allons nous
limiter à ces trois mesures linéaires.
Ce deuxième chapitre étant celui consacré
à la description des modèles de machine Learning car au
début nous avons signifié que c'est un domaine qui n'est pas cher
à nous. Dans le chapitre suivant, nous allons essayer de classer et
grouper les données qui nous servirons dans la construction du nouveau
modèle de prédiction de séjour hospitalier, le principal
objectif de ce travail.
43
| 


