III.4. APPRENTISSAGE DES RESEAUX DE NEURONES
L'apprentissage est une phase du développement d'un
réseau de neurones durant laquelle le comportement du réseau est
modifié jusqu'à l'obtention du comportement désiré.
L'apprentissage neuronal fait appel à des exemples de comportement.
L'apprentissage est dit supervisé lorsque le
réseau est forcé à converger vers un état final
précis, en même temps qu'un motif lui est présenté.
A l'inverse lors d'un apprentissage non supervisé, le réseau est
laissé libre de converge vers n'importe quel état final lorsqu'un
motif lui est présenté. Il arrive souvent que les exemples de la
base d'apprentissage comportent des valeurs approximatives ou bruitées.
Si on oblige le réseau à répondre de façon quasi
parfaite relativement à ses exemples, on peut obtenir un réseau
qui est biaisé par des valeurs erronées, et là on parle de
sur apprentissage.
III.4.1. Définition
L'apprentissage dans le contexte des réseaux de
neurones, est le processus de modification des poids de connexions (y compris
les biais) ou plus rarement du nombre de couches et de neurones (Man et Halang,
1997), afin d'adapter le traitement effectué par le réseau
à une tache particulière.
III.4.2. Apprentissage par minimisation de l'erreur
Soit E l'ensemble d'apprentissage. On considère un
réseau dont la couche de sortie comporte P cellules. Soit ( ) Les poids de la kè cellule à un instant
donné. L'erreur commise par cette cellule sur l'ensemble E, (( ) Les poids de la kè cellule à un instant
donné. L'erreur commise par cette cellule sur l'ensemble E, (( )) est définie comme étant la moyenne des erreurs
quadratique commise sur chaque forme. )) est définie comme étant la moyenne des erreurs
quadratique commise sur chaque forme.
Xi , ci (wk(t)) :,
C(wk(t)) = 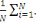 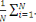 Ci (wk(t)) = Ci (wk(t)) = 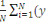 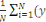 k (Xi't) - Yik)2 k (Xi't) - Yik)2
Où (????, ??) est la sortie de la
Kè cellules au temps t en fonction de l'entrée Xi.
L'apprentissage consiste donc simplement à rechercher
un vecteur 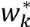 qui minimise C. La méthode proposée par Widrow et Hoff
pour résoudre ce problème consiste à adapter une
méthode d'optimisation bien connue : La minimisation par descente en
gradient. Le principe en est simple l'opposé du gradient C par rapport qui minimise C. La méthode proposée par Widrow et Hoff
pour résoudre ce problème consiste à adapter une
méthode d'optimisation bien connue : La minimisation par descente en
gradient. Le principe en est simple l'opposé du gradient C par rapport
au poids enW(t)k , -   wC (w(t)k) pointe dans la direction
dans laquelle la diminution de (????) est maximale ; en modifiant
le vecteur poids, par itération successives, dans la direction
opposée au gradient, on peut espérer aboutir à un minimum
de (????). wC (w(t)k) pointe dans la direction
dans laquelle la diminution de (????) est maximale ; en modifiant
le vecteur poids, par itération successives, dans la direction
opposée au gradient, on peut espérer aboutir à un minimum
de (????).
Le gradient de la fonction coût par rapport à
????se calcul aisément par :
C (wk(t)) = 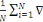 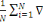 wCi (wk(t)) = wCi (wk(t)) = 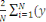 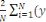 k (Xi't) - Yik).Xi k (Xi't) - Yik).Xi
Et l'algorithme d'apprentissage par descente en gradient est
donc le suivant :
Etape 0 : t=0
Initialiser aléatoirement les poids (??)
Etape 1 : Pour chaque automate sur l'ensemble d'apprentissage
E :
??(????(??))
Etape 2 : Pour chaque automate K, modifier les poids par :
(?? + 1) = ????(??)-?. ???(????(??))
Etape 3 : t = t+1
Si la condition d'arrêt non remplie, aller à
l'étape 2.
Avec ? Taux d'apprentissage.
En résumé soit
E(  ) = ) = 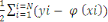 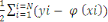 2 2
L'erreur d'apprentissage due aux poids. Si la fonction
d'activation est linéaire, cette erreur E s'écrit :
E(  ) = ) = 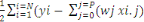 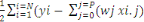 2 2
On voit donc que l'erreur E est un parabolique dans l'espace
des poids. Donc, E possède un seul minimum et il s'agit de trouver la
valeur des poids correspondant à ce minimum. Pour cela, la technique
classique consiste à utiliser un algorithme de descente de gradient.
Pour cela, on part d'un point (dans l'espace des poids, espace de dimension
P+1)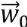 : ensuite, itérativement, on corrige ce point pour se rapprocher
du minimum de E. Pour cela, on corrige chaque poids d'une quantité
proportionnelle au gradient de E en ce point, cela dans chaque direction, donc
par rapport à chacun des poids. Ce gradient est donc la
dérivée (partielle) de E par rapport à chacun des points.
Reste à déterminer le coefficient à appliquer à
cette correction. : ensuite, itérativement, on corrige ce point pour se rapprocher
du minimum de E. Pour cela, on corrige chaque poids d'une quantité
proportionnelle au gradient de E en ce point, cela dans chaque direction, donc
par rapport à chacun des poids. Ce gradient est donc la
dérivée (partielle) de E par rapport à chacun des points.
Reste à déterminer le coefficient à appliquer à
cette correction.
?? ? ?? - ?????(?? ) ?(?? )
Il nous reste à calculer ce terme général
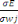 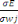 : :
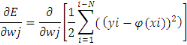
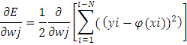
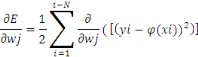
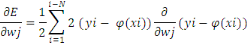
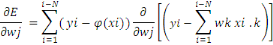
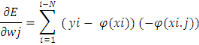
D'où :
??=??
?????= ???(????-
??(????))????.????=1
| 


