III.3.8.4. Réseaux bouclés
Un réseau dynamique ou récurrent possède
la même structure qu'un réseau multicouche munie de
rétroactions. Les connexions rétroactives peuvent exister entre
tous les neurones du réseau sans distinction, ou seulement entre
certains neurones (les neurones de la couche de sortie et les neurones de la
couche d'entrée ou les neurones de la même couche par exemple).
Les figures suivantes montrent deux exemples de réseaux
récurrents. Le premier est un simple multicouche qui utilise un vecteur
d'entrée qui contient les copies des activations de la couche de sortie
du réseau et le deuxième est un réseau à
mémoire se distingue du premier par la présence des unités
mémoires.
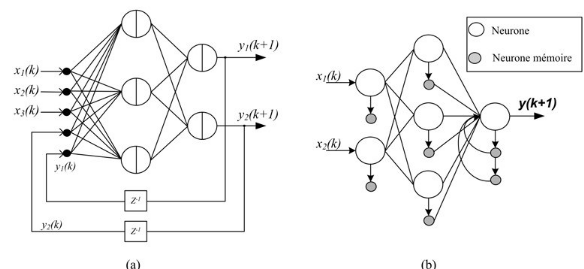
Figure 3.21: réseau de
neurones bouclé.
Le comportement collectif d'un ensemble de neurones permet
l'émergence de fonctions d'ordre supérieure par rapport à
la fonction élémentaire du neurone. Imaginer de prime abord un
tel comportement n'est pas facile, nous nous appuyons sur un exemple
illustratif et donc réductionniste.
Soit un réseau multicouche composé de 361 (19 x
19), 25 et 361 neurones. Ce réseau a appris à associer à
la lettre « a » présentée en entrée la
même lettre en sortie. Présentons au réseau cette lettre
avec quelques erreurs : un certain nombre de pixels ont été
inversé (ils sont passés de blanc à noir ou inversement).
L'image est composée de 19 x 19 pixels, chacun de ces pixels est
associé à un neurone de la couche d'entrée. Chacun des 25
neurones de la couche cachée reçoit 361 connexions (une pour
chaque neurone d'entrée) et envoie sa sortie à chacun des
neurones de la couche de sortie (au nombre de 361). Dans notre exemple, la
couche cachée se compose de 25 neurones, mais ce nombre, à la
différence des couches d'entrée et de sortie, n'est pas
impératif. Il y a donc 2* 361*25= 18050 connexions dans le
réseau.
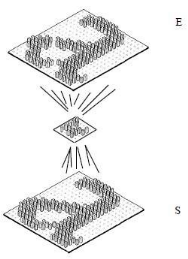
Figure 3.22: Comportement en
phase de reconnaissance d'un réseau de neurone multicouche lors d'une
tâche d'auto-association.
Les neurones sont binaires. La valeur d'activation de chaque
neurone est indiquée par la hauteur de la colonne. Les neurones sont
rangés par couche, tous les neurones d'une couche sont connexités
à tous les neurones de la couche suivante (avale). La topologie de deux
réseaux directement connectés :
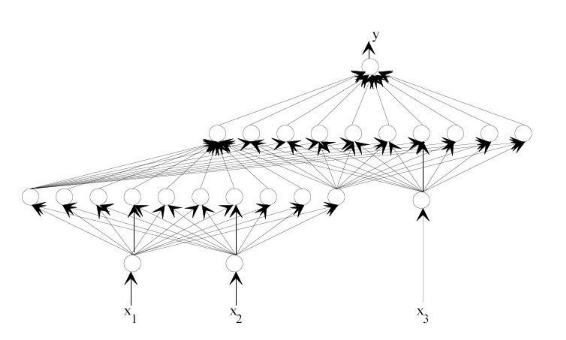
Figure 3.23: Réseaux de
neurones interconnectés.
| 


