III.2.2. Théorème
de Hyugens
On appelle inertie totale 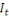 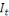 d'un nuage d'un nuage 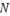 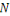 la somme pondérée des carrés des distances de ses
points au centre de gravité du nuage. Donc, si la somme pondérée des carrés des distances de ses
points au centre de gravité du nuage. Donc, si   est le centre de la classe zk, l'inertie totale de est le centre de la classe zk, l'inertie totale de 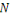 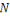 est donnée par : est donnée par :
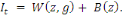
L'idée de l'algorithme de   -means est de partitionner les données de -means est de partitionner les données de 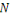 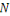 afin de: afin de:
· Minimiser l'inertie interclasse pour obtenir
des classes (cluster en anglais) les plus homogènes
possibles ;
· Maximiser l'inertie interclasse afin d'obtenir des
sous-ensembles bien différenciés.
III.2.3. Principe
général des méthodes des centres mobiles
La méthode des centres mobiles due à Forgy
[Forgy, 1965] est la plus classique et très utilisée. Elle
procède comme suit : dans une première étape, elle
consiste à tirer aléatoirement   individus de la population. Ces individus représentent les
centres provisoires des individus de la population. Ces individus représentent les
centres provisoires des   classes qui formeront la partition initiale. Ensuite, les autres
individus sont regroupés autour de ces classes qui formeront la partition initiale. Ensuite, les autres
individus sont regroupés autour de ces   centres en affectant chacun d'eux au centre le plus proche. centres en affectant chacun d'eux au centre le plus proche.
L'étape suivante consiste à recalculer les   nouveaux centres (dites aussi centroïdes ou centres de
gravité) des nouveaux centres (dites aussi centroïdes ou centres de
gravité) des   classes, sachant qu'un centre n'est pas nécessairement un
individu de la population. Le processus est répété
plusieurs fois jusqu'à stabilité des centres des classes (les
centres ne bougent plus). Comme tout les algorithmes de partitionnement, la
méthode des centres mobiles cherche à minimiser l'inertie
intraclasse définie par la somme des écarts des centroïdes
aux points de leurs classes et donc à maximiser aussi l'inertie
interclasse de la partition donnée par la somme des écarts entre
les centres des classes et le centre de la population totale (d'après le
théorème de Huygens : inertie totale = inertie intraclasse +
inertie interclasse). En minimisant l'inertie intraclasse, la méthode
des centres mobiles a tendance à chercher des classes sphériques,
d'égal volume et de faible inertie. classes, sachant qu'un centre n'est pas nécessairement un
individu de la population. Le processus est répété
plusieurs fois jusqu'à stabilité des centres des classes (les
centres ne bougent plus). Comme tout les algorithmes de partitionnement, la
méthode des centres mobiles cherche à minimiser l'inertie
intraclasse définie par la somme des écarts des centroïdes
aux points de leurs classes et donc à maximiser aussi l'inertie
interclasse de la partition donnée par la somme des écarts entre
les centres des classes et le centre de la population totale (d'après le
théorème de Huygens : inertie totale = inertie intraclasse +
inertie interclasse). En minimisant l'inertie intraclasse, la méthode
des centres mobiles a tendance à chercher des classes sphériques,
d'égal volume et de faible inertie.
Cette méthode a connu des améliorations comme la
méthode des   -moyennes ( -moyennes (  -means) de Mac Queen. Avec l'approche -means) de Mac Queen. Avec l'approche   -means, les centres sont recalculés après chaque
affectation d'un individu dans une classe, plutôt que d'attendre
l'affectation de tous les individus avant de mettre à jour les centres.
Cette approche conduit généralement à de meilleurs
résultats que la méthode des centres mobiles et la convergence
est également plus rapide. -means, les centres sont recalculés après chaque
affectation d'un individu dans une classe, plutôt que d'attendre
l'affectation de tous les individus avant de mettre à jour les centres.
Cette approche conduit généralement à de meilleurs
résultats que la méthode des centres mobiles et la convergence
est également plus rapide.
III.2.4. Déroulement de l'algorithme
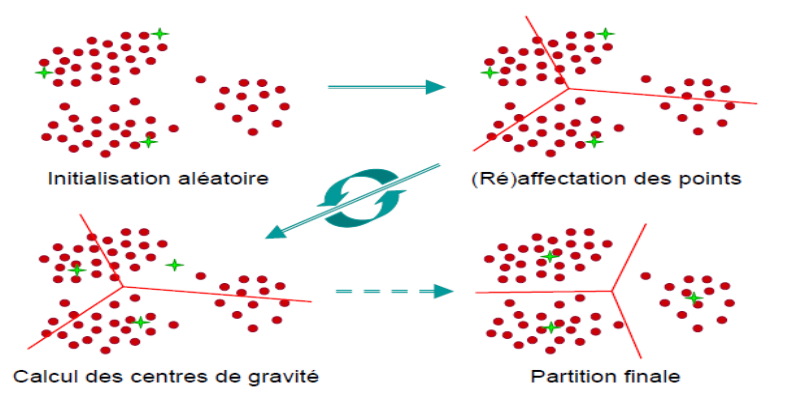
Figure 14: Déroulement de
l'algorithme de centre mobile.
Cet algorithme se déroule de la façon suivante
:
1. Initialisation :   points tirés au hasard pour les centres de gravités
(ou centroïdes) points tirés au hasard pour les centres de gravités
(ou centroïdes)
de chaque classe ;
2. Affectation : On affecte les points à la classe
la plus proche ;
3. Représentation : On recalcule les nouveaux
centres de gravités,
4. Itération : On répète les
étapes d'affectation et de représentation jusqu'à
la
convergence de l'algorithme (i.e. plus de changement de
partition).
Les expériences montrant que le nombre
d'itérations nécessaires à l'algorithme pour converger est
assez fiable. Cet algorithme est adapté à des tableaux des
grandes tailles, sa complexité étant linéaire.
| 


