III.2. ALGORITHME DE   -MEANS [2], [15] -MEANS [2], [15]
III.2.1. Introduction
Les algorithmes des centres mobilesvisent à
diviser un ensemble de données en différents
« paquets » homogènes, en ce sens que les
données de chaque sous-ensemble partagent des
caractéristiques communes, qui correspondent le plus souvent à
des critères de proximité (ou similarité) que l'on
définit en introduisant des mesures et classes de distance entre
individus.
Étant donnés des points et un
entier   , le problème est de diviser l'ensemble de , le problème est de diviser l'ensemble de   individus du nuage des points individus du nuage des points 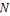 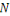 en en   groupes, souvent appelés clusters ou classes, de
façon à minimiser une certaine fonction. On considère la
distance d'un individu à la moyenne des individus de sa classe ; la
fonction à minimiser est la somme des carrés de ces distances. groupes, souvent appelés clusters ou classes, de
façon à minimiser une certaine fonction. On considère la
distance d'un individu à la moyenne des individus de sa classe ; la
fonction à minimiser est la somme des carrés de ces distances.
Ainsi, la similarité à l'intérieur d'un
même groupe est élevée mais faible entre les
différentes classes. Pour ce faire ces algorithmes itèrent en
deux étapes, d'abord ils calculent les centres des groupes,
deuxièmement, ils assignent chaque objet au centre le plus proche.
Chaque classe est caractérisée par le centre ou prototype et par
ses éléments. Le prototype des classes est le point de l'espace
de dimension   ( (  correspond au nombre de descripteurs) où la somme des distances
à tous les objets d'un même groupe est minimale. Avec la
méthode de centre mobile classique, lors d'une itération
donnée, le calcul des centres se fait après l'affectation des
individus dans leurs classes respectives. Mais avec correspond au nombre de descripteurs) où la somme des distances
à tous les objets d'un même groupe est minimale. Avec la
méthode de centre mobile classique, lors d'une itération
donnée, le calcul des centres se fait après l'affectation des
individus dans leurs classes respectives. Mais avec   -means qui est une variante de centre mobile, dès qu'on affecte
un individu dans une classe, on recalcule directement le centre, ce qui
accélère convergence de l'algorithme. -means qui est une variante de centre mobile, dès qu'on affecte
un individu dans une classe, on recalcule directement le centre, ce qui
accélère convergence de l'algorithme.
Le   -means repose généralement sur des algorithmes
simples, et permet de traiter rapidement des ensembles d'effectif assez
élevé en optimisant localement un critère. Il consiste
à minimiser le critère suivant : -means repose généralement sur des algorithmes
simples, et permet de traiter rapidement des ensembles d'effectif assez
élevé en optimisant localement un critère. Il consiste
à minimiser le critère suivant :
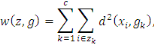
Où 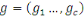 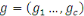 , ,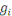 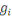 est le centre de la classe zk. Rappelons que le
critère W(z,g), qui est simplement la somme des inerties des c classes,
est appelé inertieintra classe. La méthode des centres mobiles
consiste à chercher la partition telle que le W soit minimal pour avoir
en moyenne des classes bien homogènes, ce qui revient à chercher
le maximum de l'inertie interclasse, est le centre de la classe zk. Rappelons que le
critère W(z,g), qui est simplement la somme des inerties des c classes,
est appelé inertieintra classe. La méthode des centres mobiles
consiste à chercher la partition telle que le W soit minimal pour avoir
en moyenne des classes bien homogènes, ce qui revient à chercher
le maximum de l'inertie interclasse,
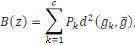
Avec   le centre de gravité du nuage et le centre de gravité du nuage et 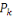 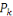 est le poids de la classe zk. est le poids de la classe zk.
In fine, l'inertie intraclasse est la mesure de la dispersion
d'individus dans la même classe, tandis que l'inertie interclasse est la
mesure de la dispersion de centres de classes différentes.
| 


