L'angle limite est la valeur de l'angle incident i1 à
partir duquel il y a réflexion totale.
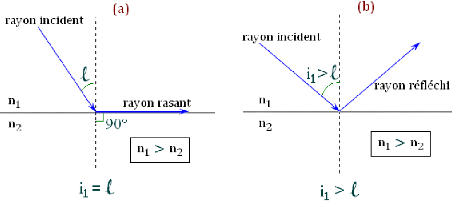
On remarque que pour n1 > n2, le rayon réfracté
s'écarte de la normale lorsqu'on augmente
progressivement la valeur de l'angle d'incidence. Quand l'angle
de réfraction arrive à 90°, l'angle d'incidence atteint sa
limite c'est-à-dire la valeur minimum sur laquelle il n'y a pas de
rayon réfracté. Au-delà de cet angle
limite, noté t le faisceau réfracté
disparait car le faisceau incident est alors entièrement
réfléchie (Figure 1.06b). On parle
alors de « réflexion totale ». [7]
12
Figure 1.06 : a) Le faisceau réfracté
n'existe plus ; b) Le faisceau incident est entièrement
réfléchi.
Pour i1 = t on a i2 = 90°
La relation (1. 03) permet d'écrire :
n1.sin t = n2.sin 90°
(1.07)
Ce qui entraine :
sin t = (1.08)
Finalement, l'angle limite s'écrit :
t = arcsin
(1.09)
( )
Par exemple, si la lumière passe d'un verre quelconque
d'indice n1=1,5 dans l'air d'indice n2=1,
alors l'angle limite est tel que sin t
= . Il est alors proche de 42°.
Ainsi,
o Si l'angle d'incidence est inférieur à 42°,
le faisceau est réfracté dans l'air ;
o S'il vaut 42°, il est alors rasant ;
o S'il est plus grand que 42°, il est entièrement
réfléchi par l'air et reste dans le verre.
13
La condition de guidage est la condition pour que tous les rayons
circulant dans la fibre optique soient réfléchis par la gaine.
Elle est obtenue par la relation :
i1 > arcsin (nn
2', (1.10)



