A. CALCUL DE H ET

Figure 61 : les efforts dans le câble principal et
pylône

Figure 62 : chargement du câble principal Vue la
symétrie nous considérons une partie de la structure
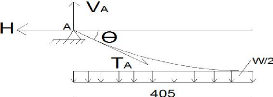
Figure 63 : chargement du demi-câble
principal
91
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
92
TRAVAIL DE FIN D'ETUDE
W = ? = , = 77,61 t m
W = = , = 38,8 t m
?M = H Y =0
En remplaçant X par L/2, on a : H =
= ,
= 47148,075 t
,
V = V =
= = 31432,05 t
,
tg = = , =0,66 =33,69
En A, la pente de la tangent au câble est égale
à 33,69° La traction en A dans le câble sera égale
à
T = vV H = v31432,05 47148,075 = 56664,93 t
|
,
Ou T = -- =
,
|
= 56664,889 t
|
tg â = = 1,25 ? â = 51,34
,
T = = ,
= 75473,429 t
B. CALCUL DE LA FORCE DE COMPRESSION DANS LE POTEAU
La compression dans le poteau AE sera égale à

Figure 64 : effort de compression du pylône
92
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
93
TRAVAIL DE FIN D'ETUDE
P = T sin T sin â = 56664,889 sin 33,69 75473,429 sin
51,34
P = 90366,658 t = 903666580 N
A = ,
= 2967263,397 mm
Nous adoptons une section carrée : a = b = 2000 mm = 2
m
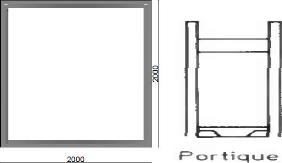
Figure 65 : la section du portique
Nous avons deux pylônes en portique
C. CALCUL DE LA LONGUEUR DU CABLE ENTRE A ET B
On sait que le câ le prend la forme para olique sous
l'action des charges verticales W uniformément distribuées.
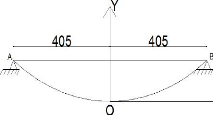
Figure 66 : la longueur du câble principal
L'équation de la parabole est donnée par : Y = a
X
Pour : X = 0 ; Y = 0
X = = 405 m ; Y = flèche maximale du câble à
mi portée
,
93
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
94
TRAVAIL DE FIN D'ETUDE
Y = a X si X = et Y =
= a ( ) ? a = ? Y = X ? Y' = ? Y =
On sait que : ds = vdx dy
= v1 Y dx
La longueur du câble est donnée par : S = 2 ? ds = 2
? v1 Y dx
[
S = 2 ? 1 dx= v X ln (X v X )
S = 4759,94 m 4760 m
D. CABLE PRINCIPAL
T = 56664,93 t = 566649300 N
A = , = 1860639,493 mm
Nous adoptons : A = 1.860.700 mm
D = v = v4 , = 1539,58 mm
Nous considérons : D = 1540 mm et A = 1.861.706 mm
E. CABLE TENDU
T = 75473,429 t = 754734290 N
A = ,
= 2478231,997 mm
Nous adoptons : A = 2.478.232 mm
D = v = v4 . .
, = 1776,79 mm
Nous considérons : D = 1778 mm et A = 2.481.607,94 mm
? VERIFICATION DES STABILITES
1. EVALUATION DES CHARGES VERTICALES 1.1. POIDS PROPRE DE
LA SEMELLE
P = 60 15 2,5 = 2250 t m
X = = 30 m
94
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
95
TRAVAIL DE FIN D'ETUDE
1.2. POIDS DE LA SUPERSTRUCTURE
P = P P P P P é
- P = 450 24 810 = 8748000 kg = 8748 t
- P = 7,8 0,0116 810 = 73,288 t
- P = 7,8 0,0116 24 = 2,17152 t
- P = 1,155 2 810 = 1871,1
t
- P é = 345,5 24 810 = 6716,520 t
P = 17411 t ? P = = 21,5 t/m
X = = 30 m
1.3. REACTION DES CHARGES
P = T S (P P ) = 14,6 3,06 = 11,54 t
P = , = 0,4808
X = = 30 m
? TABLEAU RECAPITULATIF DES CHARGES
VERTICALES
Tableau N° 22 : les charges verticales
|
CHARGES
|
EFFORTS
|
BRAS DE LEVIER
|
MOMENTS
|
|
P
|
2250
|
30
|
67500
|
|
P
|
21,5
|
30
|
645
|
|
P
|
0,4808
|
30
|
14,424
|
|
E V = 2271,98 t
|
|
E M =68159,424 tm
|
2. EVALUATION DES CHARGES HORIZONTALES
2.1. POUSSEE DUE A LA SURCHARGE DU REMBLAI
H = Q h K or K = tg ( ) avec =
30
K = tg ( ) = 0,33
Q = 1 t m h = 15 m
H = 1 60 0,33 = 19,8 t m X = = 7,5 m
95
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
96
TRAVAIL DE FIN D'ETUDE
2.2. POUSSEE DES TERRES
H = h K= 1,8 15 = 202,5
X = = 5 m
2.3. EFFORT DE FREINAGE
=
H
Avec k = 0,33 ; C = 56 t ; n = 6 et l = 24 m
H = , = 4,62
X = 15 m
> TABLEAU RECAPITULATIF DES CHARGES HORIZONTALES
Tableau N° 23 : les charges horizontales
CHARGES
|
EFFORTS
|
BRAS DE LEVIER
|
MOMENTS
|
H
|
19,8
|
7,5
|
148,5
|
H
|
202,5
|
5
|
1012,5
|
H
|
4,62
|
15
|
69,3
|
|
? H = 226,92 t
|
|
? M =1230,3 tm
|
|
> STABILITE AU GLISSEMENT Condition à
vérifier : 0,75 ?
? 1,5 ? 0,75 , , = 7,5 1,5
Donc pas de glissement
> STABILITE AU RENVERSEMENT
Condition à vérifier : ? 1,5 ? , = 55,4 1,5
? ,
Donc pas de renversement
> STABILITE A LA CAPACITE PORTANTE
Pour que la résistance passe par le tiers central, il faut
que la condition suivante soit vérifiée : e
- = = 10 m
96
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
97
TRAVAIL DE FIN D'ETUDE
Comparaison : e = 9,8 m 10 m ; donc la résultante passe
par le tiers central
|
?
|
CALCUL DES CONTRAINTES
|
|
|
|
|
=
|
?
|
(1
|
)
|
=
|
, (1 ,
|
)
|
=
|
74,89
|
|
|
|
|
|
|
|
|
=
|
?
|
(1
|
)
|
=
|
,
(1
|
)
|
=
|
|
|
|
|
|
|
|
0,75
|
DIAGRAMME DES CONTRAINTES :

Figure 67 : le diagramme des contraintes
? LES ASSEMBLAGES
Nous allons utiliser les boulons à haute adhérence
(HR)
Nous allons faire le dimensionnement des boulons par rapport aux
plus grands efforts dans les barres.
Nous avons :
- un gousset de 8 mm d'épaisseur : t = 8 mm
- effort dans les barres : N
- Classe de boulon : acier S335
- La limite d'élasticité d'un acier : f = 335
- Coefficient de frottement des pièces : = O, 3O
- = = 1,25
- Boulon HR10.9
- La section brute de profilé : A
- La section nette minimale : A =
- La section de perçage : Ù = A A
- La résistance au glissement des boulons
F = or F = 0,7 f A
- Nombre des boulons : n =
- La pression diamétrale : F = ,
97
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
98
TRAVAIL DE FIN D'ETUDE
- La vérification : F F
| 


