SECTION 3
|
Y = 0,7
0,7 = Y
7 3,6
|
? Y = 0,36
|
|
Y = Y = 0 SECTION 4
|
Y = 0,6
0,6 = Y
6 2,6
|
? Y = 0,26
|
|
Y = Y = 0
82
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
83
TRAVAIL DE FIN D'ETUDE
SECTION 5
|
Y = 0,5
0,5 = Y
5 1,6
|
? Y = 0,16
|
|
Y = Y = 0

SECTION 6
|
Y = 0,4
0,4 = Y
4 0,6
|
? Y = 0,06
|
|
Y = Y = 0
83
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
84
TRAVAIL DE FIN D'ETUDE
SECTION 7

Y = 0,3
Y = Y = Y = 0
SECTION 8
Y = 0,2 et Y = Y = Y = 0
SECTION 9
Y = 0,1 et Y = Y = Y = 0
SECTION 10
Y = Y = Y = Y = 0
TABLEAU DES VALEURS DES ORDONNEES DUES AU
CONVOI
Tableau N°19 : calcul des lignes d'influence des
entretoises
section
|
Y
|
Y
|
Y
|
Y
|
9Y
|
19Y
|
14Y
|
14Y
|
?9 Y
19Y 14Y 14Y )
|
0,566 ? 9Y
19Y 14Y 14Y
|
0
|
1
|
0,66
|
0,06
|
0
|
9
|
12,54
|
0,84
|
0
|
22,38
|
12,66
|
1
|
0,9
|
0,56
|
0
|
0
|
8,1
|
10,64
|
0
|
0
|
18,74
|
10,6
|
2
|
0,8
|
0,46
|
0
|
0
|
7,2
|
8,74
|
0
|
0
|
15,94
|
9,02
|
3
|
0,7
|
0,36
|
0
|
0
|
6,3
|
6,84
|
0
|
0
|
13,14
|
7,43
|
4
|
0,6
|
0,26
|
0
|
0
|
5,4
|
4,94
|
0
|
0
|
10,34
|
5,85
|
5
|
0,5
|
0,16
|
0
|
0
|
4,5
|
3,04
|
0
|
0
|
7,54
|
4,26
|
6
|
0,4
|
0
|
0
|
0
|
3,6
|
0
|
0
|
0
|
3,6
|
2,03
|
7
|
0,3
|
0
|
0
|
0
|
2,7
|
0
|
0
|
0
|
2,7
|
1,52
|
8
|
0,2
|
0
|
0
|
0
|
1,8
|
0
|
0
|
0
|
1,8
|
1,01
|
9
|
0,1
|
0
|
0
|
0
|
0,9
|
0
|
0
|
0
|
0,9
|
0,509
|
10
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
84
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
85
TRAVAIL DE FIN D'ETUDE
VALEURS DES EFFORTS TRANCHANTS
Tableau
N°20 : calcul des efforts tranchants
Section
|
S
|
S
|
S
|
S (P
P )
(1)
|
S q (2)
|
S q (3)
|
Convoi (4)
|
Effort
(5)
|
0
|
5
|
0
|
5
|
3,06
|
12
|
0
|
12,66
|
27,72
|
1
|
4,05
|
0,05
|
4
|
2,448
|
9,72
|
0,0285
|
10,6
|
22,79
|
2
|
3,2
|
0,2
|
3
|
1,836
|
7,68
|
0,114
|
9,02
|
18,65
|
3
|
2,45
|
0,45
|
2
|
1,224
|
5,88
|
0,256
|
7,43
|
14,79
|
4
|
1,8
|
0,8
|
1
|
0,612
|
4,32
|
0,456
|
5,85
|
11,238
|
5
|
1,25
|
1,25
|
0
|
0
|
3
|
0,712
|
4,26
|
7,972
|
6
|
0,8
|
1,8
|
- 1
|
-0,612
|
1,92
|
1,026
|
2,03
|
4,364
|
7
|
0,45
|
2,45
|
-2
|
-1,224
|
1,08
|
1,396
|
1,52
|
2,772
|
8
|
0,2
|
3,2
|
-3
|
-1,836
|
0,48
|
1,824
|
1,01
|
1,478
|
9
|
0,05
|
4,05
|
-4
|
-2,448
|
0,12
|
2,308
|
0,509
|
0,489
|
10
|
0
|
5
|
-5
|
-3,06
|
0
|
2,85
|
0
|
-0,21
|
|
T = 27,72 t = 27720 Kg = 277200 N
? DIMENSIONNEMENT DES POUTRES ET ENTRETOISES A. LES
POUTRES
Le dimensionnement se fait à la flexion :
Notre section est de classe 4 (IPE 300 à 600). IPE 500 et
f = 335 MPA
Condition : le moment fléchissant M dans chaque section
transversale doit être inférieur au moment résistant, soit
: M = M
Avec : M = ; = 1,1 et M = 68,81 tm = 6881 * 10 Nmm
,
On aura : M = M = ? W =
W 2259432,836 mm
Nous adoptons : W = 2441 10 mm Nous avons le profilé IPE
550
85
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
86
TRAVAIL DE FIN D'ETUDE
B. LES ENTRETOISES
W
Avec : M = 52,3 tm = 523 10 Nmm
W = = 1717313 mm
,
Nous adoptons : W = 1728 10 mm Nous avons le profilé IPEA
500
? CALCUL DU TREILLIS
Le treillis principal

Figure 51 : La poutre du treillis la plus
chargé
Le cas le plus défavorable, la poutre transversale au
milieu qui sera la plus chargée et la poutre longitudinale de 1O
mètres de portée
l = 2 m
? EVALUATION DES CHARGES
- Le poids propre de la dalle et chaussée : G = 795,5
Kg/m
- La surcharge roulante : (9000, 19000, 14000 et 14000) Kg
- La surcharge de la foule : Q = 500
86
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
87
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
87
TRAVAIL DE FIN D'ETUDE
? CHARGE SURFACIQUE
P = 1,35 G 1,5 Q = 1,35 795,5 1,5 500 = 1823,925
P = 1823,925 l = 1823,925 2 = 3647,85 Par rapport aux charges
linéaires nous aurons

R = R = = , = 18239,25 Kg
Nous avons deux poutres identiques qui concourent vers ce noeud,
on aura : 2 R = 2 18239,25 = 36478,5 Kg
? LES CHARGES CONCENTREES
On aura : ? 1,5
|
|
P
|
1,5 *
|
1,18
|
* 9
|
=
|
15,93 t = 15930 Kg
|
1,5 *
|
1,18
|
*1
|
9
|
=
|
33,63 t = 33630 Kg
|
1,5 *
|
1,18
|
* 14
|
=
|
24,78 t = 24780 Kg
|
|
Nous aurons :
? Le 1 cas

Figure 52 : premier chargement de la poutre principale du
tablier Apres résolution nous avons les réactions d'appuis
suivant

Figure 53 : Les réactions d'appuis de la poutre
principale du ta lier
88
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
88
TRAVAIL DE FIN D'ETUDE
? Le 2 cas

Figure 54 : deuxième chargement de la poutre
principale du tablier Apres résolution nous avons les
réactions d'appuis suivant

Figure 55 : Les réactions d'appuis de la poutre
principale du ta lier La somme donne :
R = R R = 70304,4 Kg et R = R R = 87225 Kg
Nous
considérons : R = 87225 Kg
? CHARGEMENT DU TREILLIS TRANSVERASAL
Noeuds extrêmes : R R = 18239,25 87225,6 = 105464,85 Kg
Noeuds intermédiaire : 2R R = 36478,5 87225,6 = 123704,1
Kg

Figure 56 : chargement du treillis transversal
Apres résolution nous avons les résultats suivants
:

Figure 57 : les réactions d'appui du treillis
transversal
89
TRAVAIL DE FIN D'ETUDE
Les extrêmes globaux
N = 2171,50 t = 21715000 N ? DIMENSIONNEMENT
= ,
N = N = = ? A = 71302,98 mm
Nous adoptons : A = 743,7 10 mm (le profilé HE100*584
)
? CHARGEMENT DU TREILLIS LONGITUDINAL
Le treillis est sollicité par les réactions aux
appuis venant de la poutre
R = R = 785,85 t
L = 810 mètres
l = 10 mètres
Nombre des travées = 81
Nombre des suspentes = 80
? LE TREILLI CHARGE

Figure 58 : chargement du treillis longitudinal
? LES REACTIONS

Figure 59 : les réactions d'appui
R = 27343 t et R = 100 t (réaction des suspentes) Effort
dans les barres maximales : 783,06 t
89
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
90
TRAVAIL DE FIN D'ETUDE
> LE PROFILE TUBULAIRE POUR LES SUSPENTES

> DIMENSIONNEMENT
· LES BARRES
N = = ? avec N = 7830600 N
A = ,
= 25712,4 mm
Nous adoptons : A = 270 10 mm (HE600 B)
· LES SUSPENTES
A avec N = 100 t = 1.000.000 t
A , = 3283,58 mm 3284 mm
Nous aurons deux suspentes en un point de câble
principal

Figure 60: deux suspentes sur câble principal
A = 1642 mm
Nous adoptons : A = 1680 mm (D = 82,5 mm et t = 7,1 mm)
90
Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN
91
TRAVAIL DE FIN D'ETUDE
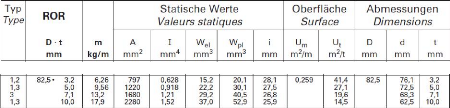
Tableau N° 21 : les caractéristiques des
profilés tubulaire
|
|



