Conception et calcul d'un pont suspendu.

A. TREILLIS DU TABLIER TRANSVERSAL

Nous les caractéristiques suivantes des boulons :

Les boulons de 30 mm de diamètre (d = 30 mm)

Le diamètre de perçage des trous de boulonnage de 32 mm (d = 32 mm)

K = 1; m = 1 ; = 0,30; f = 1000 MPA ; A = 561 mm et = 1,25
N = 2171,50 t = 21715000 N

, ,

F = ,

,

F =

,

= 94248 N

= 480000 N

n = = 231 oulons

Vérification : F = 94248 N F = 480000 N ; la condition a vérifiée B. LE TREILLIS DU TABLIER LONGITUDINAL

N = 783,06 t = 7830600 N

, F = ,				= 94248 N
	,
F = ,			= 480000 N
	,

n = = 83 oulons

Vérification : F = 94248 N F = 480000 N ; la condition a vérifiée

4.3 CONCEPTION ET PRE-DIMENSIONNEMENT DE L'INFRASTRUCTURE A. MASSIF D'ANCRAGE

Condition : P T

Or : P = V = a c

Le massif d'ancrage a une forme cu ique rectangulaire (a = = c)

C T ? C v

= v

= 31,13 m

,

,

Nous adoptons : C = 35 m

98

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

99

TRAVAIL DE FIN D'ETUDE

Si nous considérons a = b = c = 35 m, il y aura chevauchement entre les deux massifs d'ancrage.

Nous changeons les dimensions : a = 10 m et b = c = 65,25 m

Figure 68 : le massif d'ancrage

B. FONDATION

Nous avons deux pylônes sous semelle, donc une semelle filante

Figure 69 : vue en plan de la fondation

Condition :

· Aux dimensions : = ? B

or = = 2 m

(2)

B B (1)

· Aux contraintes : = B

Avec P = 903666580 N et = 3

= 30

v v

(1) = (2) : B = ?B = = = 54,88 cm

99

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

100

TRAVAIL DE FIN D'ETUDE

Nous adoptons : B = B = 60 m

h = 5 cm = 5 = 1455 cm = 14,55 m

Nous adoptons : h = 15 m

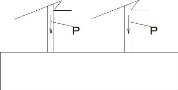
Figure 70 : coupe transversale de la fondation

,

=

G = B B h = 60 60 15 25000 = 135 10 N

=	,		= 100,8

P = B = 1008000 60 = 6,049 10 N m On aura :

Figure 71 : chargement de la semelle

Les réactions d'appui

Figure 72 : les réactions d'appui de la semelle

100

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

101

TRAVAIL DE FIN D'ETUDE

Moment

Figure 73 : diagramme de moment de la semelle
Effort tranchant

Figure 74 : diagramme des efforts tranchants de la semelle

Effort normal

Figure 75 : diagramme des efforts normals de la semelle
Déformée

Figure 76 : diagramme de la déformée de la semelle

101

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

102

TRAVAIL DE FIN D'ETUDE

Efforts

Tableau N° 24 : les valeurs des efforts intérieurs

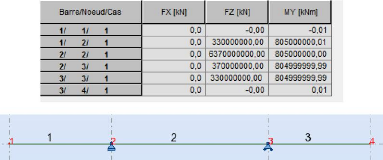
Figure 77 : les noeuds et arres de la poutre

Nous uniformisons les armatures inférieures à ceux des supérieurs (appuis et travée) par rapport au plus grand moment

M = 805000000 Nm

? CALCUL DES ARMATURES

f = 25 MPA ? f = 14,2 MPA f = 400 MPA ? f = 348 MPA a = a' = 5 cm

d = 1500 - 5 = 1495 cm

d' = d - a' = 1495 - 5 = 1490 cm M = 805000000 Nm

=			= 0,00422

,

= 0,00422 = 0,39 ; Simplement armé

= 1,25(1 V1 2 0,00422) = 0,005286 Z = 0,9 1495 = 1345,5 cm

A =

= 1719,2 cm

,

102

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

103

TRAVAIL DE FIN D'ETUDE

Section d'une arre de 40 : S = , = 12,56 cm

N = , = 136,87 137 HA 40

,

A = A = 1720,72 cm (137 HA 40)

- Armature transversal

= = 13,33 mm ? = 14 mm (HA14)

- Espacement des barres

t = 15 = 15 40 = 600 mm = 60 cm ? t = 20 cm ? PLAN D'ARMATURE

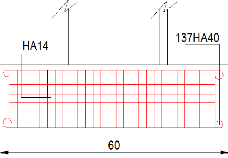
Figure 78 : plan d'armature de la semelle ? LES RESULTATS FINALS

Figure 79 : la description du pont suspendu coté

103

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

104

TRAVAIL DE FIN D'ETUDE

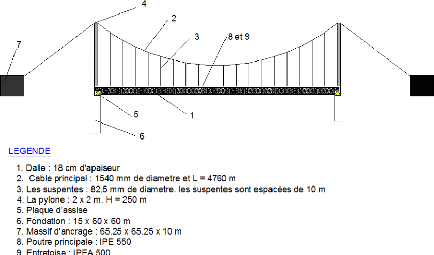
Figure 80 : les nomenclatures et dimensions des éléments du pont

Figure 81 : la représentation du pylône coté

104

Par l'Ingénieur technicien : OTEMAKUMI LOTENGO MERLIN

105

TRAVAIL DE FIN D'ETUDE

CHAPITRE 7. ETUDES DES IMPACTS ENVIRONEMENTAUX ET EVALUATION DU PROJET