Conception et dimensionnement d'un pont en béton armé de 17,00m de portée à ériger sur la rivière Tshuenge dans la ville province de Kinshasa.

6.1.5.2. Calcul des moments fléchissant

Nous prenons pour hypothèse : La charge unitaire se déplace le long de la poutre ainsi défini en parcourant les deux sens de circulation.

^1t

^S

^{A B}

^Xs

^X

^{RA L RB}

RA = (1- ) et RB =

La somme de moment en un point est égale à zéro, nous considérons le moment à gauche de la section. Même en considérant le moment à droite, les deux auront la même valeur juste la différence de signe. Nous prenons le moment positif car nos poutres sont isostatiques non continues.

Moment à gauche de la section S : MS = RA . XS = (1- ) . XS - Si X=L ; MS = 0 m

Xs

- Si X = XS ; MS = (1- ) . XS

[36]

TABLEAU DES MOMENTS ET DES EFFORTS TRANCHANTS

TABLEAU DES MOMENTS
SECTION	XS (m)	L(m)	Ms= (1-Xs/L)Xs
0	0	17	0
1	1,7		1,53
2	3,4		2,72
3	5,1		3,57
4	6,8		4,08
5	8,5		4,25
6	10,2		4,08
7	11,9		3,57
8	13,6		2,72
9	15,3		1,53
10	17		0

Lignes d'influences longitudinales des moments fléchissant :

^1t

^S

^{A B}

^Xs

^X

^{RA L} RB

6.1.5.3. Calcul des efforts tranchants Nous considérons la même hypothèse :

[37]

Les efforts tranchants équivalent aux réactions d'appuis. Avec RA = 1- et RB =

TABLEAU DES EFFORTS TRANCHANTS
SECTION	Xs	L	RA	RB
0	0	17	1	0
1	1,7		0,9	0,1
2	3,4		0,8	0,2
3	5,1		0,7	0,3
4	6,8		0,6	0,4
5	8,5		0,5	0,5
6	10,2		0,4	0,6
7	11,9		0,3	0,7
8	13,6		0,2	0,8
9	15,3		0,1	0,9
10	17		0	1

Lignes d'influences longitudinales des efforts tranchants :

Pour déterminer l'effort tranchant max, nous considérons 3 cas :

[38]

6.1.6. Application des lignes d'influences 6.1.6.1. Lignes d'influences des moments fléchissant Pour déterminer le moment max ; nous considérons 3 cas :

1er CAS : le train de charge se trouve au milieu du pont, on considère qu'un essieu se trouve au milieu du pont et un autre à 1,5m de celui-ci.

? Section 0 : le moment est nul au niveau des appuis.

? Section 1 :

^{30t 30t}

^Y1

^Y2

^1,50

Avec : y1 = 0,85m et y2 = 0,7m ; ? Section 2 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 1,7m et y2 = 1,4m ? Section 3 :

[39]

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 2,55m et y2 = 2,1m ? Section 4 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 3,4m et y2 = 2,8m ? Section 5 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 4,25m et y2 = 3,5m ? Section 6 :

^Y1

^1,50

Y2

^{30t 30t}

[40]

Avec : y1 = 3,4m et y2 = 3,9m

> Section 7 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 2,55m et y2 = 3,00m

> Section 8 :

^{30t 30t}

> Section 9 :

^{30t 30t}

^1,50

^Y1

^1,50

^Y2

^{Y1 Y2}

Avec : y1 = 0,85m et y2 = 1,00m

> Section 10 : le moment est nul

[41]

2ème CAS : L'un de train de charge se trouve au droit de la première section et l'autre à 1,50m de celui-ci :

? Section 1 :

^{30t 30t}

^Y1

^Y2

^1,50

Avec : y1 = 1,53m et y2 = 1,38m ? Section 2 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 1,36m et y2 = 2,56m ? Section 3 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 1,19m et y2 = 2,24m ? Section 4 :

^{30t 30t}

^1,50

^Y1

^Y2

[42]

Avec : y1 = 1,08m et y2 = 1,92m ? Section 5 :

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1 = 0,85m et y2 = 1,6m ? Section 6 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 0,68m et y2 = 1,28m ? Section 7 :

[43]

^{30t 30t}

^Y1

^1,50

^Y2

Y1 Y2

Avec : y1 = 0,17m et y2 = 0,32m

Avec : y1 = 0,51m et y2 = 0,96m ? Section 8 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 0,34m et y2 = 0,68m ? Section 9 :

^{30t 30t}

^1,50

[44]

^V1

^1,50

^V2

Avec : y1 = 2,77m et y2 = 2,32m

3ème CAS : le train de charge se trouve à égale distance de l'axe du pont :

? Section 1 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1 = 0,99m et y2 = 0,77m ? Section 2 :

^{30t 30t}

^1,50

^Y2

^Y1

Avec : y1 = 1,85m et y2 = 1,55m ? Section 3 :

^{30t 30t}

[45]

? Section 4 :

^{30t 30t}

^1,50

^{Y1 Y2}

Avec : y1 = 3,7m et y2 = 3,1m ? Section 5 :

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1 = 3,87m et y2 = 3,87m ? Section 6 :

^30t

^30t

^1,50

^Y1

^Y2

Avec : y1 = 3,1m et y2 = 3,7m ? Section 7 :

[46]

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1 = 2,32m et y2 = 2,77m ? Section 8 :

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1 = 1,55m et y2 = 1,85m ? Section 9 :

^30t

^30t

^1,50

^Y2

^Y1

Avec : y1 = 0,75m et y2 = 0,92m

Les surfaces d'influences des moments donnent : S0 = S10 = 0 tm²

S1 = S9 = = 13,005 m²

S2 = S8 = = 23,12 m2

[47]

S3 = S7 = = 30,345 m²

S4 = S6 = = 34,68 m²

S5 = = 36,125 m²

6.1.6.1.1. Moments dus au convoi

^MOMENT FLECHISSANT (CONVOIS)

^SECTION

^CAS 1

^CAS 2

^CAS 3

^à retenir

^MxK

^Y2

^M=(Y1+Y2)30

^Y1

^Y2

^M=(Y1+Y2)30

^Y1

^Y2

^M=(Y1+Y2)30

^0

^0

^0

^0

^0

^0

^0

^0

^0

^0

^0

^1

^0,85

^0,7

^46,5

^1,53

^1,38

^87,3

^0,92

^0,77

^50,7

^87,3

^49,761

^2

^1,7

^1,4

^93

^1,36

^2,56

^117,6

^1,85

^1,55

^102

^117,6

^67,032

^3

^2,55

^2,1

^139,5

^1,19

^2,24

^102,9

^2,77

^2,32

^152,7

^152,7

^87,039

^4

^3,4

^2,8

^186

^1,08

^1,92

^90

^3,7

^3,1

^204

^204

^116,28

^5

^4,25

^3,5

^232,5

^0,85

^1,6

^73,5

^3,87

^3,87

^232,2

^232,2

^132,354

^6

^3,4

^3,9

^219

^0,68

^1,28

^58,8

^3,1

^3,7

^204

^219

^124,83

^7

^2,55

^3

^166,5

^0,51

^0,96

^44,1

^2,32

^2,77

^152,7

^166,5

^94,905

^8

^1,7

^2

^111

^0,34

^0,68

^30,6

^1,55

^1,85

^102

^111

^63,27

^9

^0,85

^1

^55,5

^0,17

^0,32

^14,7

^0,75

^0,92

^50,1

^50,1

^28,557

^10

^0

^0

^0

^0

^0

^0

^0

^0

^0

^0

0

[48]

6.1.6.1.2. Moments dus au poids propre

Evaluation des charges linéaires :

> Poids de la dalle : 0,18m x 12m x 25KN/m³ = 54 KN/m

> Poids de la chaussée :

- Revêtement : 0,08m x (2 x 3,50m) x 24 KN/m³ = 13,44 KN/m

- Chape d'étanchéité : 0,04m x (2 x 3,50m) x 21 KN/m³ = 5,88 KN/m

- Couche de forme : 0,04m x (2 x 3,50m) x 22 KN/m³ = 6,16 KN/m

Poids de la chaussée par mètre linéaire : P_c = 25,48 KN/m

> Poids du trottoir :

- Carrelage en dallettes : 2 x 0,04m x 1,40m x 25 KN/m³ = 2,8 KN/m

- Mortier de pose : 2 x 0,01m x 1,40m x 22 KN/m³ = 0,616 KN/m

- Sable : 2 x 0,10m x 1,40m x 18 KN/m³ = 5,04 KN/m

- Bordure externe : 2 x 0,15m x 0,30m x 25 KN/m³ = 2,25 KN/m

- Bordure interne : 2 x 0,10m x 0,15m x 25 KN/m³ = 0,75 KN/m

Poids propre du trottoir : PT = 11,456 KN/m

> Garde-corps : 2x1 KN/m = 2 KN/m

> Poids propre du séparateur : 0,205m² x 25 KN/m³ = 5,125 KN/m

> Poids propre des poutres : 4 x 1,32m x 0,50m x 25 KN/m³ = 66 KN/m

> Poids propre des goussets : 4 x 2 x 0,30m x 0,10m x 25 KN/m³ = 6 KN/m

> Poids propre des entretoises :

- Au appuis : 2 x (1,0m - 0,18m) x 0,40m x 25 KN/m³ = 16,4 KN/m

- En travée : 2 x (1,32m - 0,18m) x 0,40m x 25 KN/m³ = 22,8 KN/m

Poids propre des entretoises : PE = 39,2 KN/m

Ptotale = 54 KN/m + 25,48 KN/m + 11,456 KN/m + 2 KN/m + 5,125 KN/m + 66 KN/m+ 6 KN/m + 39,2 KN/m = 209,261 KN/m

? Ptotale = 209,261 KN/m.

La charge reprise par poutre sera : Ppoutre = = = 52,31525 KN/m

Soit Ppoutre = 5,231525 t/m

[49]

TABLEAU ES MOMENTS DUS AUX POIDS PROPRES

		^MOMENT DU AU POIDS PROPRE ^Poids propre par ^poutre(t/m)
				^SECTION
^SURFACE (m2)
				^0
^0				^1
^13,005				^2
^23,12				^3
^30,705

^5,231525

^68,03598263

^160,6339751

⁴

^34,68

⁵

^36,125

^188,9888406

⁶

^34,68

⁷

^30,705

^160,6339751

^68,03598263

6.1.6.1.3. Moment dus à la foule

La norme belge prévoit une charge de 0,4 t/m² pour la foule.

Les surfaces d'influence dans la répartition transversale ont donné :

^8 ^9 ^10 N° POUTRE	^23,12 13,005 0S+	S-		Somme	P1
2,45	0,20	2,25		P2
2,25	0	2,25		P3
2,25	0	2,25		P4
2,45	0,20	2,25

^(tm)

^{0 120,952858 181,429287 181,429287 120,952858}

⁰

Nous multiplions la charge de la foule par les surfaces d'influences ci-haut :

? PFoule : S⁺ = 2,45m x 0,4 t/m² = 0,98 t/m

[50]

? PFoule : S^- = 0,20m x 0,4 t/m² = 0,08 t/m

On retient : PFoule = 0,98 t/m

TABLEAU DES MOMENTS DU A LA FOULE

		^MOMENT DU A LA FOULE ^FOULE
				^SECTION
^SURFACE
				^0
^0				^1
^13,005				^2
^23,12				^3
^30,705

^{Mfoule=SxFoule}

^0,98

⁰

^12,7449

^22,6576

^30,0909

⁴

^34,68

^33,9864

⁵

^36,125

^35,4025

⁶

^34,68

^33,9864

⁷

^30,705

^30,0909

⁸

^23,12

^22,6576

⁹

^13,005

^12,7449

¹⁰

⁰

⁰

NB : De tous ces tableaux, c'est-à-dire celui des moments dus à la foule, des moments dus au convoi et des moments dus au poids propre seront repris dans un tableau récapitulatif duquel on tirera la valeur du moment ultime maximum (le plus contraignant). C'est cette valeur de moment ultime max qui fera l'objet des calculs d'armatures. On fait de même pour les efforts tranchants.

[51]

VOICI LE TABLEAU RECAPITULATIF

			^TABLEAU RECAPUTILATIF
						^SECTION
^MOMENT DU ^AU POIDS		^MOMENT DU ^A LA FOULE	^MOMENT DU ^AU CONVOIS	^MOMENT ULTIME ^Mu=1,35Mp+1,5(	^MOMENT DE
^PROPRE						^0
^0		^0	^0	^0		^1
^68,03598263		^12,7449	^49,761	^185,6074265		^2
^120,952858		^22,6576	^67,032	^297,8207583		^3
^160,6339751		^30,0909	^87,039	^392,5507164

^Mf+Mq)

^33,9864

^116,28

^470,3291375

^35,4025

^132,354

^506,7696848

^33,9864

^124,83

^483,1541375

^30,0909

^94,905

^404,3497164

^22,6576

^63,27

^292,1777583

^12,7449

^28,557

^153,8014265

⁰

⁰

⁰

COURBE ENVELOPPE DES MOMENTS

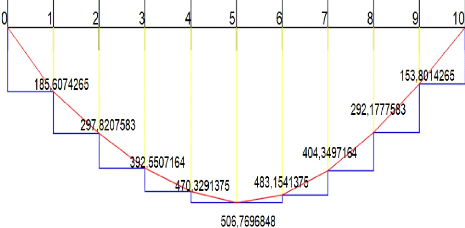
[52]

6.1.6.2. Lignes d'influences des efforts tranchants

1er CAS : : le train de charge se trouve au milieu du pont, on considère qu'un essieu se trouve au milieu du pont et un autre à 1,5m de celui-ci.

? Section 0 :

^V1

^{30t 30t}

^1,50

^V2

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m ? Section 1 :

^0.9t

^Y1

^{30t 30t}

^1,50

^Y2

^0.1t

^{30t 30t}

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m ? Section 2 :

^1,50

Y2

^Y1

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m ? Section 3 :

^{30t 30t}

^V1

^1,50

^V2

[53]

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m ? Section 4 :

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1⁺ = 0,5m et y2⁺ = 0,41m

? Section 5 :

^1,50

^V2

^{30t 30t}

^V1

Avec : y1 = y1⁺ + y1^- = 0,5m - 0,5m = 0m et y2 = 0,41m

? Section 6 :

[54]

^{30t 30t}

^1,50

^Y2

^Y1

Avec : y1^- = 0,5m et y2^- = 0,58m ? Section 10 :

Avec : y1^- = 0,5m et y2^- = 0,58m ? Section 7 :

^{30t 30t}

^1,50

^V1

^V2

Avec : y1^- = 0,5m et y2^- = 0,58m ? Section 8 :

^{30t 30t}

^1,50

^Y1

^Y2

^{30t 30t}

^1,50

^0.1t

^V1

^V2

0.9t

Avec : y1^- = 0,5m et y2^- = 0,58m ? Section 9 :

[55]

^{30t 30t}

^1,50

^Y1

^Y2

^1t

Avec : y1^- = 0,5m et y2^- = 0,58m

2ème CAS : L'un de train de charge se trouve au droit de la première section et l'autre à 1,50m de celui-ci :

> Section 0 : ^1t

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1⁺ = 0,9m et y2⁺ = 0,81m

> Section 1 :

^0.9t

^{30t 30t}

^Y1

^1,50

^Y2

^0.1t

Avec : y1 = 0,8m et y2⁺ = 0,81m

> Section 2 :

[56]

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 6 :

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 3 :

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 4 :

^{30t 30t}

^1,50

^Y1

^Y2

^{30t 30t}

^1,50

^Y1

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 5 :

^{30t 30t}

^1,50

^Y1

^Y2

[57]

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 7 :

^{30t 30t}

^V1

^1,50

^V2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 8 :

^{30t 30t}

^Y1

^1,50

^Y2

^{30t 30t}

^1,50

^0.1t

^Y1

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 10 :

Avec : y1^- = 0,1m et y2^- = 0,18m ? Section 9 :

[58]

^Y1

^1,50

^Y2

Avec : y1^- = 0,1m et y2^- = 0,18m

3ème CAS : le train de charge se trouve à égale distance de l'axe du pont :

> Section 0 :

^1t

^{30t 30t}

^1,50

^Y2

Avec : y1 = 0,54m et y2 = 0,45m

> Section 1 :

^0.9t

^Y1

^30t

^1,50

^30t

Y2

^0.1t

Avec : y1 = 0,54m et y2 = 0,45m

> Section 2 :

^Y1

[59]

^{30t 30t}

^1,50

^Y2

Avec : y1 = 0,54m et y2 = 0,45m ? Section 3 :

^30t

^1,50

^30t

^Y2

^Y1

^Y1

^{30t 30t}

^1,50

Y2

Avec : y1 = 0,54m et y2 = 0,45m ? Section 4 :

^{30t 30t}

^Y1

^Y2

^1,50

Avec : y1 = 0,54m et y2 = 0,45m ? Section 5 :

[60]

Avec : y1^- = 0,50m et y2⁺ = 0,45m ? Section 6 :

^30t

^1,50

^V2

^V1

Avec : y1^- = 0,45m et y2^- = 0,54m ? Section 7 :

^30t

^{30t 30t}

^Y1

^1,50

^Y2

Avec : y1^- = 0,45m et y2^- = 0,54m ? Section 8 :

^{30t 30t}

^1,50

^'f1

^'f2

Avec : y1^- = 0,45m et y2^- = 0,54m ? Section 9 :

[61]

^{30t 30t}

^1,50

^0.1t

^Y1

^Y2

Avec : y1^- = 0,45m et y2^- = 0,54m ? Section 10 :

^30t

^30t

^Y1

^1,50

^Y2

Avec : y1^- = 0,45m et y2^- = 0,54m

Les surfaces d'influences des efforts tranchants donnent :

S0^+ =	m	S10 - =	m
	= 8,5		= 8,5t
S1^+ =	= 6,885 m	S9^- =	= 6,885 m
S2^+ =	m	S8^- =	m
	= 5,44		= 5,44
S3^+ =	m	S7^- =	m
	= 4,165		= 4,165
S4^+ =	m	S6^- =	m
	= 3,06		= 3,06
S5^+ =	m	S5^- =	m
	= 2,125		= 2,125
S6^+ =	m	S4^- =	m
	= 1,36		= 1,36
S7^+ =	= 0,765 m	S3^- =	= 0,765 m

[62]

S8^+ =	=	0,34 m	S2^-	=	=	0,34 m
S9^+ =	=	0,085 m	S1^-	=	=	0,085 m
S10^+ = 0 m			S0^-	= 0 m

6.1.6.2.1. Efforts tranchants dus au convois

^EFFORTS TRANCHANT (CONVOIS)
^SECTION	^CAS 1			^CAS 2			^CAS 3			^à retenir	^TxK
	^Y1	^Y2	^T=(Y1+Y2)30	^Y1	^Y2	^T=(Y1+Y2)30	^Y1	^Y2	^T=(Y1+Y2)30
^0	^0,5	^0,41	^27,3	^0,9	^0,81	^51,3	^0,54	^0,45	^29,7	^51,3	^29,241
^1	^0,5	^0,41	^27,3	^0,9	^0,81	^51,3	^0,54	^0,45	^29,7	^51,3	^29,241
^2	^0,5	^0,41	^27,3	^-0,1	^-0,18	^-8,4	^0,54	^0,45	^29,7	^29,7	^16,929
^3	^0,5	^0,41	^27,3	^-0,1	^-0,18	^-8,4	^0,54	^0,45	^29,7	^29,7	^16,929
^4	^0,5	^0,41	^27,3	^-0,1	^-0,18	^-8,4	^0,54	^0,45	^29,7	^29,7	^16,929
^5	^0	^0,41	^12,3	^-0,1	^-0,18	^-8,4	^-0,5	^0,45	^-1,5	^12,3	^7,011
^6	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	^-18,468
^7	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	^-18,468
^8	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	^-18,468
^9	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	^-18,468
^10	^-0,5	^-0,58	^-32,4	^-0,1	^-0,18	^-8,4	^-0,45	^-0,54	^-29,7	^-32,4	-18,468

[63]

6.1.5.2.2. Efforts tranchants dus au poids propre

			^P propre
^SECTION	^S+	^S-		T+= ^S+ Ppropre
^0	^8,5	^0		^44,4679625
^1	^6,885	^0,085		^36,01904963

^{EFFORTS TRANCHANTS DUS AU POIDS PROPRE}

^0,34

^28,459496

^0,765

^21,78930163

6.1.5.2.3. Efforts tranchants dus à la foule

^4 ^3,06 ^1,36 ^16,0084665
^5	^2,125	^2,125	^5,231525	^11,11699063
^6	^1,36	^3,06	^EFFORTS TRANCHANTS DUS AU POIDS PROPRE ^P Foule ^0,98	^7,114874
^7	^0,765	^4,165		^4,002116625
^8 ^SECTION	^0,34 ^S+	^5,44 ^S-		^1,7787185 T+= ^S+ Ppropre	^T- = ^S- Ppropre
^9 ^0	^0,085 ^8,5	^6,885 ^0		^0,444679625 ^8,33	^0
^10 ^1	^0 ^6,885	^8,5 ^0,085		^0 ^6,7473	^0,0833
^2	^5,44	^0,34		^5,3312	^0,3332
^3	^4,165	^0,765		^4,0817	^0,7497
^4	^3,06	^1,36		^2,9988	^1,3328
^5	^2,125	^2,125		^2,0825
^6	^1,36	^3,06		^1,3328
^7	^0,765	^4,165		^0,7497

[64]

TABLEAUX RECAPITULATIF DES EFFORTS TRANCHANTS Efforts tranchants positifs

^SECTION	^T propre	^T foule	^T convois	^T= 1,35Tp + ^1,5(Tf + ^Tc)
^0	^44,4679625	^8,33	^29,241	^116,3882494
^1	^36,01904963	^6,7473	^29,241	^102,608167
^2	^28,459496	^5,3312	^16,929	^71,8106196

^{TABLEAU RECAPITULATIF DES EFFORTS TRANCHANTS POSITIFS}

^4,0817

^16,929

^4,0817

^16,929

^2,0825

^7,011

Efforts tranchants négatifs

^6 ^7,114874 ^1,3328 ^-18,468 ^-16,0977201
^7	^4,002116625	^0,7497	^-18,468	^-21,17459256
^8	^1,7787185	^0,3332	^-18,468 ^TABLEAU RECAPITULATIF DES EFFORTS TRANCHANTS NEGATIFS	^-24,80093003
^9 ^SECTION	^0,444679625 ^T propre	^0,0833 ^T foule	^-18,468 ^T convois	^-26,97673251 ^T= 1,35Tp + ^1,5(Tf + ^Tc)	^Tserv
^10 ^0	^0 ^0	^0 ^0	^-18,468 ^-18,468	^-27,702 ^-27,702	^-18,468
^1	^0,444679625	^0,0833	^-18,468	^-26,97673251	^-17,94002038
^2	^1,7787185	^0,3332	^-18,468	^-24,80093003	^-16,3560815
^3	^4,002116625	^0,7497	^-18,468	^-21,17459256	^-13,71618338
^4	^7,114874	^1,3328	^-18,468	^-16,0977201	^-10,020326
^5	^11,11699063	^2,0825	^7,011	^28,64818734	^20,21049063
^6	^16,0084665	^2,9988	^16,929	^51,50312978	^35,9362665
^7	^21,78930163	^4,0817	^16,929	^60,93160719	^42,80000163
^8	^28,459496	^5,3312	^16,929	^71,8106196

[65]

COURBE ENVELOPPE DES EFFORTS TRANCHANTS

6.2. Calcul de l'entretoise

L'entretoise se calcul comme une poutre reposant sur une(des) poutre(s)s principale(s) :

^Entretoises

^{3m 3m 3m}

^Poutre

1er Cas : On applique une charge unitaire au milieu du pont ; on constate que toutes les poutres sont chargées de la même façon, d'une charge de 0,25t

[66]

^{d1 1t}

^{0,25t 0,25t 0,25t 0,25t}

MO = 0,25t (3m + 1,5m) + 0,25t (1,5m) = 1,125tm + 0,375tm = 1,5 tm

2eme Cas : On applique une charge unitaire au droit de la poutre P1 ; on constate que les poutres ne sont plus chargées de la même façon :

^1t

^{0,70t 0,40t 0,10t 0,20t}

MO = 0,70t (3,0m + 1,5m) + 0,40t (1,5m) - 1t (3,0m + 1,5m) = - 0,75tm

Lignes d'influences des moments au centre du pont :

^{0,75tm 0,75tm}

- -

^{1,5m 6,0m 1,5m}

+

1,5tm

[67]

Pour le calcul de surfaces d'influences nous considérons les valeurs en ordonnées adimensionnelles alors les surfaces d'influences de l'entretoise donnent :

? S⁺ = = 4,5 m²

? S^- = 2( = - 1,125 m²

6.2.1. Calcul des moments

6.2.1.1. Moments dus aux charges permanentes

Ce sont les charges fixes et le poids propre. Ces éléments ne causent pas de flexion de l'entretoise. Ces charges sont reprises par les poutre principales. Tout le pont fléchi et les entretoise restent parallèles à elles-mêmes.

6.2.1.2. Moments dus à la charge de la foule La charge de la foule prévue par la norme est de 0,4 t/m.

Le coefficient dynamique : õ = 1,14

On trouve les lignes d'influences de la réaction de l'entretoise suite à l'action de la dalle considérée isostatiquement liée à l'entretoise.

^{Sens de circulation}

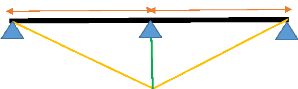
^{5,65 5,65}

^1t

la charge repartie de la foule sera : 0,4t/m² x 1,14 x 2( ) = 2,5764 t/m

Pour usage des lignes d'influences de moments en O. M+ = 2,5764 t/m x 4,5 m² = 11,5938 tm

M- = 2,5764 t/m x 1,125 m² = 2,89845 tm

[68]

6.2.1.3. Moments dus à la charge du convoi

Nous considérons que deux convois passent en même temps sur le pont et leurs essieux passent sur l'entretoise au même moment (cas le plus défavorable). Nous avons un convoi de 60t soit 30t par essieux. Nous avons une charge de 15t par roues espacé de 1,90m.

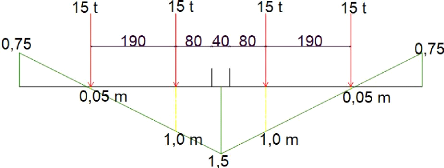
Les lignes d'influences des moments donnent : y1 = y4 = 0,05m et y2 = y3 = 1,0m ; alors le moment du au convois sera :

M ⁺convois = 15t x 1,14 x 2(0,05 + 1,0) = 35,91 tm M ^-convois = 15t x 1,14 x 2(0) = 0 tm

M⁺max = 1,5(11,5938 tm + 35,91 tm) = 71,2557 tm M^-max = 1,5(2,89845 tm + 0 tm) = 4,347675 tm