Conception et dimensionnement d'un pont en béton armé de 17,00m de portée à ériger sur la rivière Tshuenge dans la ville province de Kinshasa.

6.1.2. Evaluation des charges

> Poids de la dalle : Pdalle= ép. x l_p x L_p x ?b = 0,18m x 17m x 12m x 25KN/m³ = 918 KN

> Poids de la chaussé :

- Revêtement : 0,08m x (2x3,50m) x 17m x 24KN/m³ = 228,48 KN

- Chape d'étanchéité : 0,04 x (2x3,50m) x 17m x 21KN/m³ = 99,96 KN

- Couche de forme : 0,04 x (2x3,50m) x 17m x 22KN/m³ = 104,72 KN

Poids de la chaussé : Pchaussée = 433,16 KN

> Poids du trottoir :

- Carrelage en dallette : 2 x 0,04m x 1,40m x 17m x 25KN/m³ = 47,6 KN

- Mortier de pose :2 x 0,01m x 1,40m x 17m x 22KN/m³ = 10,472 KN

- Sable : 2 x 0,10m x 1,40m x 17m x 18KN/m³ = 85,68 KN

- Bordure externe : 2 x 0,15m x 0,30m x 17m x 25KN/m³ = 38,25 KN

- Bordure interne : 2 x 0,15m x 0,10m x 17m x 25KN/m³ = 12,75 KN

Poids du trottoir : PTrottoir = 194,752 KN

> Garde-corps : PGarde-corps = 1KN/m x 17m x 2 = 34KN > Séparateur en béton :

- Trapèze : P1 = x 0,60m x 17m x 25KN/m³ = 70,125 KN

- Rectangle : P2 = 0,40m x 0,10m x 17m x 25KN/m³ = 17 KN

Poids du séparateur : Pseparateur = 87,125 KN

> Gousset : les 2 triangles : 2 x (0,30m x 0,10m) x 17m x 25KN/m³ = 25,5 KN

Il y a 4 poutres et les goussets sont placés dans chaque poutres on a : PGousset = 25,5KN x4 =

102KN

> Poids de la poutre : Ppoutre = 4 x (1,50m - 0,18m) x 0,50m x 17m x 25KN/m³ = 1122KN

> Poids de l'entretoise :

- Aux appuis : 2 x (1m - 0,18m) x 0,40m x (12m - 3m) x 25KN/m³ = 147,6 KN - En travée : 2 x (1,32m - 0,18m) x 0,40m x (12m - 3m) x 25KN/m³ = 205,2 KN

Poids de l'entretoise : PEntretoise= 352,8 KN

[33]

6.1.3. Calcul des coefficients d'impact dynamique

õ = 1+ +

6.1.3.1. Coefficient dynamique de la dalle

[a dalle doit supporter son poids propre est toute les surcharges fixes, alors :

P1 = Pdalle + _Pchaussée + _PTrottoir + _PGarde-corps + Pseparateur = 918 KN + 433,16 KN+ 194,752KN + 34 KN + 87,125 KN = 1667,037 KN

õdalle = 1+ + ? õdalle = 1,1824128 1,2

6.1.3.2. Coefficient dynamique de la poutre

[a poutre doit supporter son poids propre, le poids de la dalle, le poids des entretoises et les surcharges fixes ; ainsi :

P2 = P1 + _Ppoutre + _PGousset + PEntretoise = 1667,037 KN + 1122 KN + 102 KN + 352,8 KN P2 = 3243,837 KN

õpoutre = 1+ + ? õpoutre = 1,14170149 1,14

6.1.4. Coefficient de répartition transversale

Nous utiliserons les lignes d'influences transversales pour déterminer les valeurs de réactions par essieux. Pour le calcul des surface d'influences, les valeurs lues en ordonnée sont considérées adimensionnelles. Nous considérons que deux convois de 60t passent au même moment sur le pont ce qui manifeste le cas le plus défavorable.

[34]

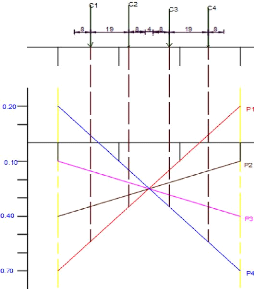
Le coefficient de répartition transversale est obtenue par la relation k = , où :

- m : le maximum des sommes de réactions par poutre due au convois

- n : le nombre d'essieux

Ces valeurs sont obtenues dans le tableau suivant :

CONVOIS	M1	M2	M3	M4	SOMME
POUTRE
P1	0,55	0,355	0,1451	-0,05	1,0001
P2	0,35	0,285	0,2149	0,15	0,9999
P3	0,15	0,2149	0,285	0,35	0,9999
P4	-0,05	0,1451	0,355	0,55	1,0001
SOMME	1	1	1	1	4

Alors : k = = 0,50005 0,5

On y affecte le coefficient dynamique de la poutre, alors on obtient un coefficient

K = k x õpoutre = 0,57

[35]

6.1.5. Calcul de la poutre la plus chargée
6.1.5.1. Calcul des efforts internes (M, N, T)

Pour déterminer, nous allons subdiviser la poutre en 10 sections égales et trouver les efforts au droit de chaque section.

Pour ce faire, nous allons faire l'étude des lignes d'influences longitudinales en plaçant une charge unitaire.