Conception et dimensionnement d'un pont en béton armé de 17,00m de portée à ériger sur la rivière Tshuenge dans la ville province de Kinshasa.

5.2.3. Dalle de transition

L'épaisseur varie de 20cm à 30cm aussi, c'est ainsi que nous adoptons b = 25cm, la longueur de 4m à 6m, nous adoptons Ldt = 5m avec une pente variant de 5 à 10% nous adoptons une pente de 8%.

Fig. 7

5.2.2. Pile

Nous avons choisi la pile type colonne avec poutre chevêtre

Fig. 8

? Epaisseur de la semelle

Avec : r= 0,50m ; f=0,50m soit i = 1,00m ; B = 5,80m

? Colonnes :

La colonne aura une section circulaire de diamètre 100cm et une hauteur de 4,38m

[24]

? Poutre chevêtre :

La poutre chevêtre aura une section carré (100cm x 100cm) et une longueur de 10m.

Fig.

(dimension en cm)

[25]

5.3. Vues et coupes

PROFIL EN LONG DU PONT

(dimension en cm)

PROFIL EN TRAVERS DU PONT

[26]

CHAPITRE 6 : Dimensionnement des éléments de la superstructure

Dans ce chapitre, nous allons évaluer les charges, étudier les sollicitations dans chaque élément du tablier et pour finir, nous allons faire le calcul du béton armé.

6.1. Poutres principales

Nous allons ici faire l'étude de la répartition transversale en vue de déterminer le coefficient de répartition transversale pour trouver la poutre la plus chargé afin la stabiliser et puisque les éléments de notre pont sont symétriques toutes les poutres seront stabilisées.

6.1.1. Répartition transversale

Le but de l'étude de répartition transversale de charge est de pouvoir permettre au concepteur de projet de pont de pouvoir arriver à déterminer la part de charges que chacune des poutres reçoive suite aux charges qui leurs seront appliquées.

Cette part de charge, sera prise en compte dans le calcul sous forme d'un coefficient de majoration qu'ont appelé coefficient de répartition transversale des charges. En effet, le coefficient de répartition transversale est une valeur qui nous permet de trouver la poutre la plus chargée et de déterminer la charge qui s'applique sur cette poutre.

Le Trafic étant une série des charges ponctuelles mobiles, les efforts intérieurs dépendent de la position des véhicules ce qui fait que l'effet de chaque véhicule se calcul à l'aide des lignes d'influences. Nous prenons les hypothèses suivantes :

? La dalle reçoit les efforts dus au convoi, à la foule, et aux surcharges fixes et les transmet aux entretoises et ces derniers les transmettent aux poutres principales. En considérant que les éléments que comporte le tablier fonctionnent ou travaillent ensemble comme un corps unique.

? Le tablier reste un élément monolithique qui ne peut subir qu'une rotation et non une flexion.

NB : pour les ponts routes ; le rapport entre l'inertie des entretoises et celles des poutres doit tendre vers l'infinie cela traduit l'idée selon laquelle plus la poutre est chargée, moins l'entretoise l'est.

[27]

Fig. 9

^{P1 P2 P3 P4}

^{15 30 30 30 15}

(Dimensions en dm)

Nous prenons une charge unitaire pour trouver les équations des lignes d'influences qui nous permettrons de déterminer en lisant en abscisse la valeur de l'effet à la position de la charge.

Considérons les cas extrêmes de chargements suivantes : 1er cas : la charge unitaire P(1t) se trouve au milieu du pont.

Fig. 10

^P=1t

^{P1 P2 P3 P4}

^{15 30 30 30 15}

(Dimensions en dm)

On constatera que chaque poutre est chargée de la même façon. Tel que :

? P = charge unitaire

? n= nombres des poutres principales ? Qi= charges reprise par la poutre ? i= variant de 1 à n

ici nous avons p=1t, n= 4 et i varie de 1 à 4 ; c'est ainsi que Q1 = Q2 = Q3 = Q4

[28]

Pour trouver la contrainte, nous savons que la contrainte c'est l'action d'une charge sur l'unité de la surface. Ainsi, nous prenons les surfaces des poutres en réduisant chaque surface à l'unité. C'est de cette façon que nous avons : S1=S2=S3=S4= 1cm². Pour avoir la contrainte sur chaque poutre on prend la charge unitaire sur la somme des surfaces de chaque poutre.

D'où :

Avec : S= S1+S2+S3+S4 = 4cm²

= 0,25 t/m²

2eme cas : la charge unitaire P=1t se trouve au droit de la poutre principale 1.

Fig. 11

(Dimensions en dm)

On constatera que la charge P provoque un basculement du tablier et donc un moment en plus de sa charge unitaire. On sait qu'une force peut subir une déviation suivant son support qui tend à l'amener vers le centre de ce dernier. Ainsi, nous voulons connaitre l'effet de cette charge sur les poutres. C'est de cette façon que nous la plaçons au milieu du pont en l'associant de son moment qui est un moment de transfert.

[29]
Fig. 12

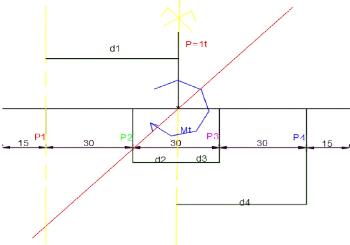
Où :

> d1 : distance de la poutre principale numéro 1 à l'axe du pont = 4,5m

> d2 : distance de la poutre principale numéro 2 à l'axe du pont = 1,5m

> d3 : distance de la poutre principale numéro 3 à l'axe du pont = 1,5m

> d4 : distance de la poutre principale numéro 4 à l'axe du pont = 4,5m

> Mt : moment de transfert = P. di

Etant donné que les poutres sont identiques nous évaluons les surfaces comme dans le premier cas où S'était égale à 4cm2.

La contrainte que recevra chaque poutre sera obtenue par la formule suivante :

Où : - Mt : le moment de transfert

- di= distance de la poutre numéro i à l'axe de la poutre

- I= moment d'inertie de la section transversale en ne considérant que les surface des poutres principales. C'est le moment de la section transversale par rapport à la charge unitaire P qui est centrée au milieu de la poutre. Elle sera obtenue par :

I= S.di

[30]

Où S est la somme des toutes les sections des poutres

Alors : I= _S1d12 + _S2d22 + _S3d32 + S4d4² = 1x (4,5)² + 1x (1,5)² + 1x(1,5)² + 1x(4,5)² I = 20,25m⁴ + 2,25 m⁴+ 2,25 m⁴ + 20,25 m⁴ = 45 m4

> Considérons que la poutre assimilée ci-dessus est d'abord soumise à l'action du moment de transfert de la charge ; alors la contrainte engendrée au droit de chaque poutre sera obtenue par :

Ainsi :

=

= 0,45t/m²

= 0 15t/m²

, =

= 0 15t/m²

, =

= 0 45t/m²

,

On sait que , alors l'effort normale sera : Ni = i x Si ; avec Si = s1+s2+s3+s4 = 1m² ;
alors : Ni = i

> Considérons cette fois que la poutre assimilée ci-dessus est soumise à la charge unitaire P, la charge Qi que reprendra chaque poutres principale (Pi) dû à l'action de Pi ; sera :

Qi = = = 0,25t

> Ainsi, en combinant les actions dues au moment de transfert et à la charge unitaire Pi , sur la poutre assimilée, l'effort total dans chaque poutres principales Pi sera donné par :

#177; Ni

Bi = #177; ou Bi =

Il est à noter que l'on additionne : Compression +compression et traction + traction On soustrait : Compression - traction et Traction - compression

[31]

Fig. 13

B1 =	#177; N1 =	+ 0,45t = 0,70 t/m^2 x 1m^2 -- P1= 0,70t
B2 =	#177; N2 =	+ 0,15t = 0,40 t/m^2 x 1m^2 -- P2= 0,40t
B3 =	#177; N3 =	- 0,15t = 0,10 t/m^2 x 1m^2 -- P3= 0,10t
B4 =	#177; N4 =	- 0,45t = - 0,20 t/m^2 x 1m^2 -- P4= -0,20t

Fig. 14

Lignes d'influences

[32]