7.5. Calcul proprement dit du mur en aile
Nous allons calculer le moment et l'effort normal par zone et
nous considèrerons la zone qui aura les valeurs les plus
élevées.
7.5.1. Calcul du corps du mur
Fig.

[109]
7.5.1.1. Calcul des moments
· Poussées des terres due au poids du sol
(H3' et H3») :
ü Pour le sable :
H'3 = (?sable x h2 x k) =
(1,8t/m3 x (4,0)2 x 0,33) x 1m = 4,752 t
Excentricité : X= (6,0 - 2,0) = 1,33 m
ü Pour le sable limoneux :
Contrainte horizontale : óh =
· -
· v
avec óv = (2,6 t/m3 x 2m ) = 5,20
t/m2
óh = - v = 0,838 t/m2
H»3 = (0,838 t/m2 x 2m ) x 1m =
0,838 t
Excentricité : X= (2m) = 0,67m
· Poussée de terres due à la
surcharge (H4) : H4 = k x V2 x Hculée = 0,40 x 1t/m2
x 6,0 m x 1m = 2,4 t Excentricité : X= (6,0m) = 3,0m
TABLEAU DES MOMENTS
TABLEAU ZONE 1 -
1
|
Zone 1 -
1
|
CHARGE
|
Excentricité
|
MOMENT
|
H2
|
0,68
|
0,85
|
0,578
|
H3
|
0,858
|
1,13
|
0,96954
|
Somme
|
1,538
|
|
1,54754
|
|
[110]
TABLEAU ZONE 2 - 2
|
Zone 2 - 2
|
CHARGE
|
Excentricité
|
|
H2
|
1,32
|
1,65
|
|
H3
|
3,234
|
2,2
|
|
Somme
|
4,554
|
|
|
|
MOMENT
2,178 7,1148
9,2928 TABLEAU ZONE 3 -
3
Zone 3 - 3
CHARGE
Excentricité
MOMENT
H2
2
2,5
H3
13
3,33
43,29
Somme
15
48,29
7.5.1.2. Calcul de l'effort normal
L'effort tranchant correspond au poids propre soit NS = 10 t
7.5.2. Calcul de la semelle
5
La semelle est sollicitée par toutes les charges
situées au-dessus c'est-à-dire : le poids du
corps du mur en aile, le poids du remblai et son poids propre ;
en dessous par la réaction du
sol. Le principe de calcul reste le même que celui de la
semelle de la culée.
Calcul des moments :
Tronçon A - B :
13,265 t/m2

10,7
17,122 t/m2
1,60 m
,
0,018 t/m
[111]
FAB1 = x 1m = x 1m = 2,034 t ; x= (1,60) = 1,06m
FAB2 = 10,722 t/m2 x 1,60m x 1m = 17,155 t ; x =
(1,60) = 0,80m FAB = 2,034 t + 17,155 t = 19,189 t
Excentricité : X = = 0,827 m
MAB = - FAB x X = - 19,189 t x 0,827 m = - 15,869 tm
Tronçon B - C :

6,909 t/m2
2,4 m
10,722 t/m2
FBC1 = x 1m = " " x 1m = 4,575 t ; x= (2,4) = 0,8mFB = 6,909
t/m2 x 2,40m x 1m = 16,581 t ; x = (2,40) = 1,20m
FBC = 4,575 t + 16,581 t = 21,156 t
Excentricité : X = = 1,11 m
MBC = - FBC x X = - 21,156 t x 1,11 m = - 23,483
tm
[112]
7.6. Piles
Fig.

Les sollicitations sur la pile se calculera par bande d'un
mètre.
7.5.1. Evaluation des charges
? Charges verticales : ? Poids
des terre (P3)
P3(gauche) = b x h x ?sable = 2,40m x (2,80m - 0,50m) x 2,60
t/m3 x 1m = 14,35 t P3(droite) = b x h x ?sable = 2,40m x (2,80m -
0,50m) x 2,60 t/m3 x 1m = 14,35 t
Excentricité : Xdrroite = (2,40m) = 1,6 m et Xgauche =
(2,40m) + 1m + 2,40 m = 4,2m ? Poids de la semelle (P2)

[113]
S1 = S4 = x 2 = 1,2 m2 ; S2 = S5 = (0,50m x 2,40m)
x 2 = 2,4 m2 et S3 = 1,00m
x 1,00m = 1,00m2
? = 1,2 m2 + 2,4 m2 x 1,00 m2 =
4,6 m2 P2 = 4,6 m2 x 2,5 t/m3 x 1 m = 11,5
t
Excentricité : X1 = (2,40m) + 1m + 2,40m = 4,2m ; X2 =
(2,40m) + 1m + 2,40 m = 4,6 m ; X3 = (1,00 m) + 2,40 m = 2,9 m ; X4 = (2,40m) =
1,6 m ; X5 = (2,40m) = 1,2 m
?
X = ? = 4,96 m
? Poids de la colonne(P1) :
P1 = x 4,38 x 2,5 t/m3 = 8,595 t ; on a 4 colonnes
alors P1 = 8,595 t x 4 = 34,38 t
P1 = x 1m = 2,865 t
Excentricité : X = (1m) + 2,40 m = 2,9 m
? Poids de la poutre chevêtre(P4) : P4 =
1m x 1m x 2,5t/m3 x 6m = 15 t
Excentricité : X = (1m) + 2,40 m = 2,9 m
? Réaction verticale due à l'action des
charges (V1) : L'effort tranchant max en ELS : Tmax = 82,0389625 t
Comme il y a 4 appuis sur la pile, on obtient :
V1 = x 1m = 27,34632 t
La pile recevra le double de cette réaction. Soit V1 =
27,34632 x 2 = 54,6926 t Excentricité : X = (1m) + 2,40
m = 2,9 m
? Charges horizontales
Le coefficient des poussées des terres k est donné
par :
[114]
Pour le sable limoneux : Nõ = tg2(45+ ) =
tg2(45+ ) = 2,46 ; k = = = 0,40
? Effort de freinage (H1) :
H1 =
Avec : - k : coefficient des poussées des terres =
0,40
- N : nombre de bandes = 2 - C : convois : 60t
- lp : largeur du pont = 12 m
H1 = x 1m = 4 t
Nous considérons le cas où deux convois freinent
simultanément sur une voie de circulation.
Alors : H1 = 2 x 4 t = 8 t Excentricité : X = 5,38 m
? Poussée des terres due au poids du sol (H2)
:
? Pour le sable limoneux :
Contrainte horizontale : óh = - v avec
óv = (2,6 t/m3 x 2,80m ) = 7,28 t/m2
óh = - v = 1,684 t/m2
H2 = (1,684 t/m2 x 2,80m ) x 1m =
2,357 t Excentricité : X= (2,80m) = 0,93m
Etant donné qu'il y a des terres de mêmes natures
de part et d'autre de la pile ; les poussées dues à ces premiers
s'annulent et maintient la pile en équilibre.
? Poussée hydrodynamique(H2) :
La poussée hydrodynamique sera évaluée
en fonction du PHE (profondeur des hautes eaux ; soit 1,20 m).
H2 = h x b x W x ?eau x V2
[115]
Avec :
· h : la hauteur de l'eau (1,20m)
· b : la largeur de l'obstacle (1m)
· W : le coefficient de forme dépendant du type
de pile (W=0,32 ; section circulaire)
· ?eau : le poids spécifique de l'eau (1
t/m3)
· V : la vitesse d'écoulement de l'eau (V =
0,9177m/s)
H2 = 1 (1,20) x (1) x (0,32) x (1 t/m3) x
(0,9177)2 = 0,1616 t
Excentricité : X = (1,20m) = 0,4 m
|
CHARGES VERTICALES
|
|
Type de charge
|
Charges
|
Excentricité
(m)
|
Moment
tm
|
|
P1
|
2,865
|
2,9
|
8,3085
|
|
P2
|
11,5
|
4,96
|
57,04
|
|
P3(gauche)
|
14,35
|
1,6
|
22,96
|
|
P3(droite)
|
14,35
|
4,2
|
60,27
|
|
P4
|
( t )
15
|
2,9
|
stabilisant en
43,5
|
|
V1
|
54,6926
|
2,9
|
158,60854
|
|
somme
|
112,7576
|
|
350,68704
|
|
CHARGES HORIZONTALES
|
|
Type de charge
|
Charges
|
Excentricité
(m)
|
Moment
tm
|
|
H1
|
8
|
5,38
|
43,04
|
|
H2
|
( t )
0,1616
|
0,4
|
renversant en
0,06464
|
|
somme
|
8,1616
|
|
43,10464
|
7.5.2. Etude de la stabilité
E Ms 350,68704
? Stabilité au renversement : , Mr = 2 ?
43,10464 = 2 ? 8,13 = 2 ; la condition
est vérifiée.
[116]
?
v Stabilité au glissement : > 2 =
2 ? 13,81 = 2 ; la condition est
vérifiée.
v Stabilité face aux contraintes transmise par le
sol :
La pile travaille en flexion composée. D'où :
? ?
ómax X (1 + ) et ómin = x (1 - )
· Calcul de l'excentricité (e) : e
= - x
? ?
=
or x=
?
= 2,7278 m
e = - 2,7278 m = 0,1722 m
condition : 0 ? e = ? 0 ? 0,1722 = 6 ? 0 ? 0,1722 = 0,966
condition vérifiéel'excentricité se trouve dans
le noyau central.
· Vérification des contraintes :
ómax = x (1 + ) = 22,904 t/m2
ómin = x (1 - ) = 15,977 t/m2
· Diagramme de contrainte :

ómin = 15,977
t/m2
ómax =
22,904 t/m2
[117]
7.5.3. Calcul proprement dit de la pile
7.5.3.1. Calcul de la poutre chevêtre
La poutre chevêtre se calculera comme une poutre reposant
sur 4 colonnes (appuis). Elle ne va supporter que son poids propre parce que
les colonnes qui composent la pile sont placées au droit des appareils
d'appuis. Les charges du tablier seront transmises directement sur les
colonnes, ce qui manifeste le cas le plus défavorable.
Le poids propre de la poutre est donné par : P4 = 1m x
1m x 2,5 t/m3 = 2,5 t/m
D'où le schéma statique
suivant :

2,5 t/m
3m 3m 3m
? Calcul des moments aux appuis :
?
Tronçons A-B-C :
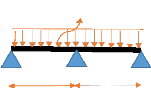
2,5 t/m
3m 3m
3MA + 2( 3+3) MB + 3MC = - ( 2,5 x 33 + 2,5 x
33 )
? 3 MA + 12 MB + 3 MC = - ( 67,5 + 67,5 )
? 3 MA + 12 MB
+ 3 MC = - ( 135)
? 3 MA + 12 MB + 3 MC = - 33,75 ? 12 MB + 3 MC = - 33,75 (1) ?
Tronçons B-C-D :

[118]
2,5 t/m
3m 3m
3MB + 2( 3+3) MC + 3MD = - ( 2,5 x 33 + 2,5 x
33 )
-- 3 MB + 12 MC + 3 MD = - ( 67 + 67 )
-- 3 MB + 12 MC +
3 MD = - ( 135)
-- 3 MB + 12 MC + 3 MD = - 33,75
3 MB + 12 MC = - 33,75 (2)
On obtient le système
suivant :
12 MB + 3 MC = - 33,75 (1)
3 MB + 12 MC = - 33,75 (2)
Après résolution du système, on a les
valeurs des moments aux appuis :
MA = 0 tm ; MB = - 2,25 tm ; MC = - 2,25 tm ; MD = 0 tm
? Calcul des moments en travées :
? Travée A-B :
2,5 t/m

MC MD
3m
MAB = - MA = - 0 = 1,8 tm
TAB = + = + = 3 t
TBA = + = + = 4,5 t
MDC = - MD = - 0 = 1,8 tm
[119]
MBA = - MB = - 2,25 = 1,8 tm
Position Mmax : XAB = = 1,2 m et XBA = = 1,8 m
> Travée B-C
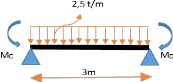
TBC = + = + = 3,75 t
TBC = + = + = 3,75 t
MBC = - MB =
- 2,25 = 0,5625 tm
MBC = - MB =
- 2,25 = 0,5625 tm
Position Mmax : XBC = = 1,5 m et XCB = = 1,5 m
> Travée C-D

TCD = + = + = 4,5 t
TDC = + = + = 3 t
MCD = - MC =
- 2,25 = 1,8 tm
[120]
Position Mmax : XCD = = 1,8 m et XDC = = 1,2 m
Diagrammes : ? Moments :

+ + +
2,25 tm 2,25 tm
- -
0,5625 tm
1,8 tm 1,8 tm
? Efforts tranchants :
3 t 3,75 t 4,5 t
+
4,5 t 3,75 t
3 t
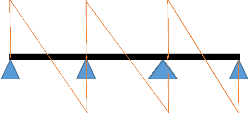
+
+
-
TABLEAUX RECAPITULATIFS
|
-
-
|
|
|
|
|
|
|
Travée
travée en tm
|
AB
|
BC
|
TABLEAU RECAPITULATIF DES MOMENTS
CD
|
A retenir Mtmax
|
|
Moments en
|
1,8
|
0,5625
|
1,8
|
|
1,8
|
|
Appuis
appuis en tm
|
A
|
B
|
C
|
D
|
|
[121]
TABLEAU RECAPITULATIF DES EFFORTS
TRANCHANTS
4,5
3
7.5.3.2. Calcul de la colonne
Travée
AB
BC
CD
Tmax
A GAUCHE
(t)
3
3,75
4,5
Les colonnes reçoivent la charge de la superstructure par
l'intermédiaire
des appareils d'appuis. Pour calculer une colonne, on
considèrera la part de charge qui lui est
transmise par la poutre avec laquelle elle est reliée et
cela se fait en flexion composée (E.L.S)
en considérant le moment à la base de la colonne.
Elle devra supporter :
A DROITE
(t)
4,5
3,75
? Son poids propre (P1) ;
? La réaction due à l'action des charges (V1), pour
une poutre ;
? Le poids propre de la poutre chevêtre (P4) ;
? Evaluation des sollicitations sur la colonne
- Poids propre de la colonne : P1 = 8,595 t ;
- La réaction due à l'action des charges
:
L'effort tranchant max(ELS) : Tmax = 82,0389625 t
Comme il y a 2 appuis sur la colonne de la pile, on obtient :
V1 = 82,0389625 t x 2 = 164,0779 t
- Réaction due au poids de la poutre
chevêtre :
V3 = Efforts tranchants = 3,75 + 4,5 t = 8,25 t ; Pour
la colonne la plus chargée
? L'effort normal (NS) :
- Charges permanentes (G) ;
G = 8,595 t + 8,25 t = 16,845 t
- La charge d'exploitation (Q) :
Q = 164,0779 t
[122]
D'où : - NS = 16,845 t +164,0779 t = 180,9229 t ?
Moment
Le moment à la base de la colonne est donné par
:
MH1 = H1 x hcolonne = 8 t x 4,38m = 35,04 tm
MH2 = H2 x (heau) = 0,1616 t x 0,4m = 0,06464 tm
MS = MH2 + MH1 = 35,04 tm + 0,06464 tm = 35,10464 tm
7.5.3.3. Calcul de la semelle
Calcul des moments :
Tronçon A - B :
22,904 t/m2
0,018 t/m

19,4405 t/m2
17122 t/m2
2,5
2,90 m
FAB1 = x 1m = x 1m = 5,022 t ; x= (2,9) = 1,93m
FAB2 = 19,4405 t/m2 x 2,9m x 1m = 56,377 t ; x = (2,9) = 1,45m
FAB = 5,022 t + 56,377 t = 61,399 t
Excentricité : X = = 1,489 m
MAB = - FAB x X
= - 61,399 t x 1,489 m = - 91,423 tm
[123]
Tronçon B - C :

15,977 t/m2
2,9 m
19,4405 t/m2
FBC1 = x 1m = x 1m = 5,022 t ; x= (2,9) = 0,96m
FB = 15,977 t/m2 x 2,9m x 1m = 46,333 t ; x = (2,9) =
1,45m FBC = 5,022 t + 46,333 t = 51,355 t
Excentricité : X = = 1,402 m
MBC = - FBC x X
= - 51,355 t x 1,402 m = - 71,999 tm
[124]
7.6. Calcul d'armatures des éléments de
l'infrastructure Nous considérons la fissuration
préjudiciable.
? Dalle de transition
ü Moment en travée (sens de X) :
MS = 16,958 tm ; d = h - e = 25cm - 5cm = 20 cm ; b = 1m ; fbs =
1800 t/m2 ; fs = 25000t/m2 ;
· Paramètre de déformation : á =
|
·
|
=
|
= 0,544
|
|
|
|
· Bras de levier : Z = d (1 - ) = 0,20(1 - ) = 0,1637m
· Sections d'armature : AS =
= = 0,004143 m2 = 41,43 cm2 soit
14HA20/m -- 43,96 cm2
ü Moment en travée (sens de Y) :
MS = 5,0875 tm ; d = 20 cm ; b = 1m ; fbs = 1800 t/m2
; fs = 25000 t/m2 ;
· Paramètre de déformation : á =
|
·
|
·
|
= 0,544
|
|
|
· Bras de levier : Z = d (1 - ) = 0,20(1 - ) = 0,1637m
· Sections d'armature : AS =
= = 0,001243 m2 = 12,43 cm2 soit
5HA18/m -- 12,72 cm2
ü Moments aux appuis :
MS = - 9,9755 tm ; d = 20 cm ; b = 1m ; fbs = 1800
t/m2 ; fs = 25000 t/m2 ;
· Paramètre de déformation : á =
|
·
|
=
|
= 0,544
|
|
|
|
· Bras de levier : Z = d (1 - ) = 0,20(1 - ) = 0,1637m
· Sections d'armature : AS =
= = 0,002437 m2 = 24,37 cm2 soit
8HA20 -- 25,14 cm2
· Espacements :
[125]
Stx < min {3 < min { ? Stx < 33cm l'espacement entre
les barres principales d'une
dalle ne dépasse pas 30 cm.
Sty < min { < min { ? Sty < 44cm.
? Culée
Les armatures se calculerons par bande d'un mètre en
flexion composé. ? Corps de la culée et mur garde
grève
Le moment le plus défavorable a été obtenu
dans la zone 3-3 d'où : MS = 65,05 tm ;
Tmax(ELS) = 82,0389625 t
R = x 1m = x 1m = 27,346320 t
NS = R + P4 + P1 = 27,346320 t + 1,84 + 7,605 = 36,79132 t b =
1m ; a = 1m ; h = 5,0 m ; fbs = 1800 t/m2 ; fs = 25000
t/m2
· Calcul du flambement : Lf = 2 x h = 2 x 5,0m = 10 m
ë = v = v = 34,64 ? 35 ; il n'y a pas risque de
flambement.
· Calcul de l'excentricité :
e1 = = = 1,768 m
ea = max { } =
{ } = { } = 2 cm = 0,02 m
e2 = ~~ x (2+(á x õ)) = ~~~ x
(2+(0,5 x 2)) = 0,018 m
et = e1 + e2 + e3 = 1,768 m + 0,02 m + 0,018 m = 1,806 m
· Coefficient de remplissage :
Ø1 = ; avec: Nmax = b x h x fbs = 1m x 5,0m x 1800 t/m2 =
9000 t
[126]
Ø1 = = 0,00408 ? 0,81
· Excentricité critique :
|
·
|
·
|
·
|
|
|
|
|
|
on a = 1+v9 _ 1+.~1+,/9 ,00408),00408)
Puisque Ø1 = 0,00408 ? =
3 ' 4(3 v v 0,166553
· Excentricité du noyau centrale :
enc = î x h = 0,166553 x 5,0 m = 0,832765 m ? et ;
d'où la section est partiellement comprimée ou tendue.
· Moment fictif :
Mf = Ns (e + d - ^ ) = 36,79132 t (1,806 m +
4,95m - ) = 156,583857 tm
· Paramètre de déformation : á =
|
·
|
=
|
= 0,544
|
|
|
|
· Bras de levier : Z = d (1 - ) = 4,95(1 - ) = 4,0524 m
· Section fictive :
Afictif = = = 0,001545 m2
· Section réelle d'armature :
Aréelle = Afictive - = 0,001545 m2 -
= 0,00007334 m2 = 0,7334 cm2 soit
4HA12/m
? 4,52 cm2
· Armatures transversales :
Öt = Öl = (12 mm) = 4 mm soit un cadre de
HA10
· Espacement : St = min{ } = min{ }
Alors St = 40 cm ;
soit St = 20 cm
Afin de faciliter la mise en oeuvre des armatures(ferraillage)
nous prolongeons les armatures du corps de la culée jusqu'au mur
garde-grève.
· Armature de frettage :
[127]
Nous savons que ces armatures servent à bloquer la
déformation transversale du béton qui se produit par l'effet de
poisson sous l'action d'une compression, à augmenter la
résistance à la rupture du béton. C'est ainsi que nous
adoptons les mêmes armatures transversales tout en réduisant
l'écartement soit HA10 espacées de 5cm.
? Corbeau :
MS = - 3,9465 tm ; d = h - e = 25cm - 5cm = 20 cm ; b = 1m ; fbs
= 1800 t/m2 ; fs = 25000t/m2 ;
·
|
Paramètre de déformation =
: á
|
=
|
= 0,544
|
|
|
|
Axe neutre : y = á x d = 0,544 x 0,20m
|
= 0,108 m
|
|
·
|
Bras de levier : Z = d (1 - ) = 0,20(1 -
|
= 0,1637m
)
|
|
|
|
Moment résistant : MRS = (b x y)
|
x Z = (1 x 0,108 )
|
1800 x 0,1637
|
|
MRS = 15,911 tm ? MS (simplement armée)
· Sections d'armature : AS =
= = 0,0009643 m2 = 9,643 cm2 soit
4HA18/m ? 10,18 cm2
Armatures de
répartition : Ar = ( 10,18) = 2,545 cm2 soit 4HA10/m
? 3,14 cm2 ? Vérification de l'effort
tranchant :
<
,0
< ? 39,465 < 182,60869 : condition
vérifiée
· Espacements :
Stx < min { < min { ? Stx < 33cm l'espacement entre
les barres principales d'une
dalle ne dépasse pas 30 cm
Sty < min { . {
< min ? Sty < 44cm.
[128]
? Semelle
Nous ne considérons que le tronçon B-C parce que
c'est là que la sollicitation est le plus à craindre.
MS = - 81,11691 tm ; d = 95 cm ; b = 1m ; fbs = 1800
t/m2 ; fsu = 25000 t/m2 ;
· Paramètre de déformation : á =
|
·
|
=
|
= 0,544
|
|
|
|
· Bras de levier : Z = d (1 - ) = 0,95(1 - ) = 0,777m
· Section d'armature :
AS = = = 0,004175 m2 = 41,75 cm2 soit
10HA25/m ? 49,09 cm2
· Armatures de répartitions :
ASt = ASl = (49,09) = 12,27 cm2 soit
4HA20/m -- 12,57 cm2
· Espacements :
Stx < min { < min { -- Stx < 33cm.
Sty < min { < min { -- Sty < 44cm.
? Mur en aile :
Les armatures se calculerons par bande d'un mètre en
flexion composée.
? Corps du mur
Le moment le plus défavorable a été obtenu
dans la zone 3-3 d'où :
MS = 48,29 tm ; NS = 10 t
b = 1m ; a = 1m ; h = 5,0 m ; fbs = 1800 t/m2 ;
fs = 25000 t/m2
· Calcul du flambement : Lf = 2 x h = 2 x 5,0m = 10 m
ë = v = v = 34,64 ? 35 ; il n'y a pas risque de
flambement.
[129]
· Calcul de l'excentricité :
e1 = = = 4,829 m
ea = max { } =
{ } = { } = 2 cm = 0,02 m
e2 = ~ x (2+(á x õ)) = ~~ x
(2+(0,5 x 2)) = 0,018 m
et = e1 + e2 + e3 = 4,829 m + 0,02 m + 0,018 m = 4,867 m
· Coefficient de remplissage :
T1 = ; avec: Nmax = b x h x fbs = 1m x 5,0m x 1800 t/m2
= 9000 t
T1 = = 0,0011 < 0,81
90
· Excentricité critique :
Puisque T1 = 0,0011 <
· on a î = v =
v = 0,166636
' v v '
· Excentricité du noyau centrale :
enc = î x h = 0,166636 x 5,0 m = 0,83318 m < et ;
d'où la section est partiellement comprimée ou tendue.
· Moment fictif :
Mf = Ns (e + d - ) = 10 t (4,867 m + 4,95m -
) = 73,17 tm
· Paramètre de déformation : á =
|
·
|
=
|
= 0,544
|
|
|
|
·
Aréelle = Afictive - = 0,0007222 m2 -
= 0,000322 m2 = 3,22 cm2 soit 5HA10/m
?
3,39 cm2
Bras de levier : Z = d (1 - ) = 4,95(1 - ) = 4,0524m
· Section fictive :
Afictif = = = 0,0007222 m2
· Section réelle d'armature :
[130]
· Armatures transversales :
Öt = Öl = (10 mm) = 3,33 mm soit un cadre de
HA8
· Espacement : St < min{ } = min{ }
Alors St < 40
cm ; soit St = 20 cm
Afin de faciliter la mise en oeuvre des armatures(ferraillage)
nous prolongeons les armatures du corps du mur.
? Semelle
Nous ne considérons que le tronçon B-C parce que
c'est là que la sollicitation est le plus à craindre.
MS = - 23,483 tm ; d = 95 cm ; b = 1m ; fbs = 1800
t/m2 ; fsu = 25000 t/m2 ;
· Paramètre de déformation : á =
|
·
|
=
|
= 0,544
|
|
|
|
· Bras de levier : Z = d (1 - ) = 0,95(1 - ) = 0,777m
· Section d'armature : AS =
= = 0,001208 m2 = 12,08 cm2 soit
8HA14 /m ? 12,32 cm2
· Armatures de répartitions :
ASt = ASl = (17,81) = 4,45 cm2 soit
4HA12/m ? 4,52 cm2
· Espacements :
Stx < min { <~ { 3 3 ? Stx < 33cm.
--
Sty < min { < min { ? Sty < 44cm.
[131]
? Pile
? Poutre chevêtre :
ü En travée :
MS = 1,8 tm ; d = 95 cm ; b = 1m ; fbs = 1800 t/m2 ;
fsu = 25000 t/m2 ;
|
·
|
Paramètre de déformation =
: á
|
=
|
= 0,544
|
|
|
|
·
|
Axe neutre : y = á x d = 0,544 x 0,95m
|
= 0,5168 m
|
|
|
·
|
Bras de levier : Z = d (1 - ) = 0,95(1 -
|
= 0,777m
)
|
|
|
|
·
|
Moment résistant : MRS = (b x y)
|
x Z = (1 x 0,5168
|
) 1800 x 0,777
|
MRS = 361,723 tm > MS (simplement armée)
· Section d'armature : AS =
= = 0,0000926 m2 = 0,926 cm2 nous adoptons
4HA12 ? 4,52 cm2
ü Aux appuis :
MS = 2,25 tm ; d = 95 cm ; b = 1m ; fbs = 1800 t/m2 ;
fsu = 25000 t/m2 ;
|
·
|
Paramètre de déformation =
: á
|
=
|
= 0,544
|
|
|
|
·
|
Axe neutre : y = á x d = 0,544 x 0,95m
|
= 0,5168 m
|
|
|
·
|
Bras de levier : Z = d (1 - ) = 0,95(1 -
|
= 0,777m
)
|
|
|
|
·
|
Moment résistant : MRS = (b x y)
|
x Z = (1 x 0,5168
|
) 1800 x 0,777
|
MRS = 361,723 tm > MS (simplement armée)
· Section d'armature : AS =
= = 0,0001158 m2 = 1,158 cm2 nous
adoptons 3HA12 ? 3,39 cm2
· Armatures transversales : TS = 4,5 t
[132]
La contrainte tangentielle : Tso = = = 4,7368 t/m2
Etant donné qu'on est en fissuration
préjudiciable
Tlim < min ( ; 4 MPa)
Tlim < min ( ; 4 MPa)
Tlim < min (3 MPa ; 4 MPa) Tlim = 3 MPa = 300
t/m2
Tso ? Tlim ; d'où les armature transversale droite.
.
| 


